Geometria analitica (28°)
L'iperbole equilatera ruotata

1)Generalità
Per venire incontro a numerose richieste per l'estensione dei file eseguibili, dei tipi già utilizzati in p55 e p57, per la soluzione di altri problemi di geometria analitica, si illustrano alcune routine di calcolo per la soluzione di casi diversi che possono essere utili a chi deve cimentarsi in questa interessante parte della matematica.
Una premessa è necessaria prima del prosieguo della pagina: gli algoritmi utilizzati non sono dimostrati ma soltanto implementati, a favore del calcolo automatico, in apposite routine in Visual Basic; per le dimostrazioni si rimanda agli innumerevoli testi di geometria analitica in commercio.

2)Algoritmi in V.B. per l'iperbole equilatera ruotata
Quando nell'iperbole con il centro nell'origine degli assi i coefficienti "a" e "b" sono uguali ( a = b ), si ha il caso dell'iperbole equilatera base:

X / a ² - Y / a ² = 1

i cui asintoti hanno equazioni:
yas1 = + x
yas2 = - x

Se l'iperbole base viene ruotata di 45° ha come asse l'asintoto dell'equilatera non ruotata.
La rotazione modifica l'equazione base:

X / a ² - Y / a ² = 1
che diventa:

Y = +/- k / X
dove k = a ² / 2

In questa pagina è riportato un file eseguibile che consente il tracciamento di questa nuova iperbole la cui funzione è detta "omografica".
Gli algoritmi implementati, scritti in linguaggio V.B. sono:

-dati d'ingresso:
a = Val(Text1.Text)
e = Val(Text2.Text)
If a = 0 Then GoTo fine
If e = 0 Then GoTo fine
-impostazioni di base:
b = a
-primo ramo equazione iperbole ruotata per grafica:
For x = 0.00001 To e Step 0.01
k = a ^ 2 / 2
c1 = k / x
If c1 < -e Then c1 = -e
Next x
-secondo ramo equazione iperbole ruotata per grafica:
For x = -e To 0.000001 Step 0.01
k = a ^ 2 / 2
c2 = k / x
If c2 < -e Then c2 = -e
-coordinate dei fuochi:
xf = +/- sqr( 2 * k ) ; yf = +/- sqr( 2 * k )
-equazione dell'asse iperbole ruotata
For x = -e To e Step 0.01
y = x
Next
-equazioni asintoti iperbole ruotata per grafica
y = 0
X = 0

La routine, molto semplice, ha il solo scopo di mostrare come si presenta graficamente l'iperbole equilatera ruotata al variare di "a" all'interno dei suoi asintoti ( assi cartesiani ortogonali ); come unici dati fornisce le coordinate dei fuochi e il valore del coefficiente k.

3)Esempio d'utilizzo del programma di calcolo
In questo paragrafo viene proposto un esercizio grafico la cui risoluzione è basata sul file eseguibile (eserc.omogr) .
L'esercizio mostrato in figura 1 è sviluppato per "a" = 2 e fondo scala = 10



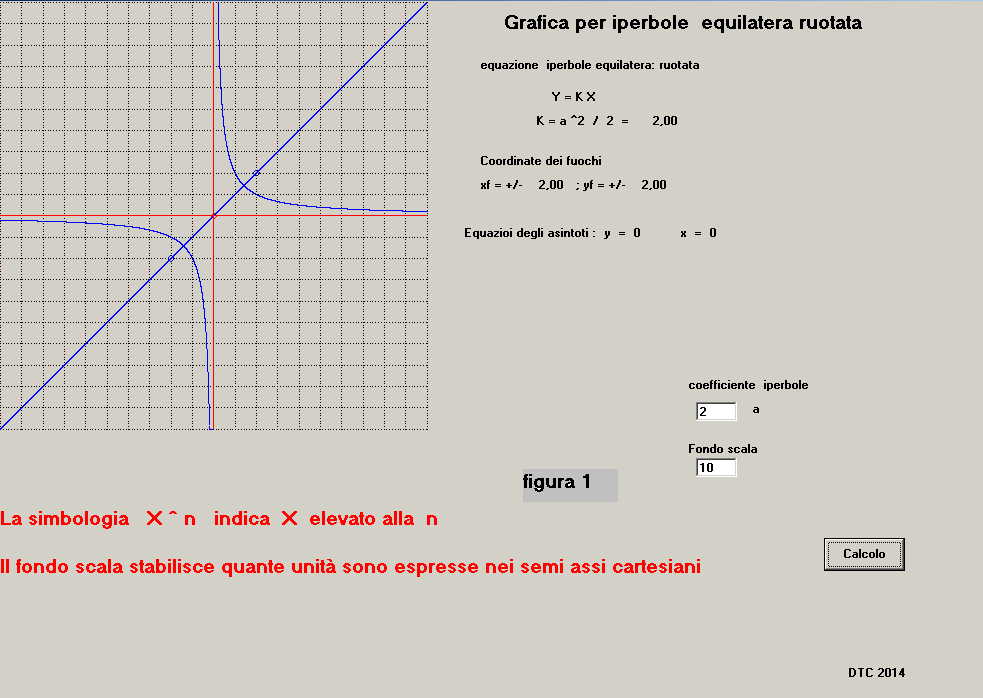
I rami dell'iperbole e il loro asse sono di colore blu, gli asintoti, ora coincidenti con gli assi cartesiani, son di colore rosso.
Il valore di k è : K = 2
Le coordinate del fuoco sono; f ( xf = +/-2 ; yf = +/-2 )

4)Note
-Il controllo software del file eseguibile è stato eseguito al meglio; è possibile però che qualche particolare anomalia sia sfuggita all'esame.
Si prega pertanto chi dovesse riscontrare qualche difetto nell'impiego del programma di renderlo noto tramite " Contatti con l'autore"; si provvederà all'aggiustaggio in rete.