Geometria analitica (29°)
Intersezioni tra iperbole equilatera ruotata e circonferenza

1)Generalità
Per venire incontro a numerose richieste per l'estensione dei file eseguibili, dei tipi già utilizzati in p55 e p57, per la soluzione di altri problemi di geometria analitica, si illustrano alcune routine di calcolo per la soluzione di casi diversi che possono essere utili a chi deve cimentarsi in questa interessante parte della matematica.
Una premessa è necessaria prima del prosieguo della pagina: gli algoritmi utilizzati non sono dimostrati ma soltanto implementati, a favore del calcolo automatico, in apposite routine in Visual Basic; per le dimostrazioni si rimanda agli innumerevoli testi di geometria analitica in commercio.

2)Algoritmi in V.B. per intersezioni iperbole equilatera ruotata e circonferenza
La presente pagina fornisce lo strumento per la soluzione automatica del problema inerente la ricerca delle coordinate dei punti dovuti all'intersezione dell'iperbole ruotata e la circonferenza con il centro nell'origine degli assi; ovvero la soluzione del sistema che vede presenti l'equazioni delle due coniche:

Y = +/- k / X (dell'iperbole ruotata)
dove k = a ² / 2

X² + Y² = R²
(della circonferenza)

Gli algoritmi implementati, scritti in linguaggio V.B. sono:

-dati d'ingresso:
a = Val(Text1.Text)
R = Val(Text2.Text)
e = Val(Text3.Text)
If a = 0 Then GoTo fine
If R = 0 Then GoTo fine
If e = 0 Then GoTo fine
-impostazioni di base:
b = a
-primo ramo equazione iperbole ruotata per grafica:
For x = 0.00001 To e Step 0.01
k = a ^ 2 / 2
c1 = k / x
If c1 < -e Then c1 = -e
Next x
-secondo ramo equazione iperbole ruotata per grafica:
For x = -e To 0.00001 Step 0.01
k = a ^ 2 / 2
c2 = k / x
If c2 < -e Then c2 = -e
-coordinate dei fuochi:
xf = +/- sqr( 2 * k ) ; yf = +/- sqr( 2 * k )
-equazione dell'asse iperbole ruotata
For x = -e To e Step 0.01
y = x
Next
-equazioni asintoti iperbole ruotata per grafica
y = 0
X = 0

-equazione circonferenza per grafica
rq = r ^ 2
For x = -r To r Step 0.001
C1 = Sqr((r ^ 2) - (x ^ 2))
C2 = -Sqr((r ^ 2) - (x ^ 2))
Next x
-soluzione sistema tra le due coniche:
If R < = a Then GoTo fine
z = (r ^ 2 - Sqr(r ^ 4 - 4 * k ^ 2)) / 2
x = Sqr(z)
z1 = (r ^ 2 + Sqr(r ^ 4 - 4 * k ^ 2)) / 2
X1 = Sqr(z1)
Y = k / x
Y1 = k / X1
Dim x11 As String
Dim y11 As String
x11 = Format((X1), "##.##")
y11 = Format((Y1), "##.##")
Label27.Caption = " X1 = +/- " + x11 + " Y1 = +/- " + y11
Dim x22 As String
Dim y22 As String
x22 = Format((Y1), "##.##")
y22 = Format((X1), "##.##")
Label28.Caption = " X2 = +/- " + x22 + " Y2 = +/- " + y22

3)Esempio d'utilizzo del programma di calcolo
In questo paragrafo sono proposti tre esercizi grafici la cui risoluzione è basata sul file eseguibile (eserc.omocirc) .

Primo esercizio per R > a: ( R = 5.7; a = 2.9 ) e fondo scala = 10:
L'esercizio, mostrato in figura 1, computati:
k = 2.9² / 2 = 4.2
R² = 5.7² = 32.49
presenta la soluzione del sistema:

Y = +/- 4.2 / X
X² + Y² = 32.49



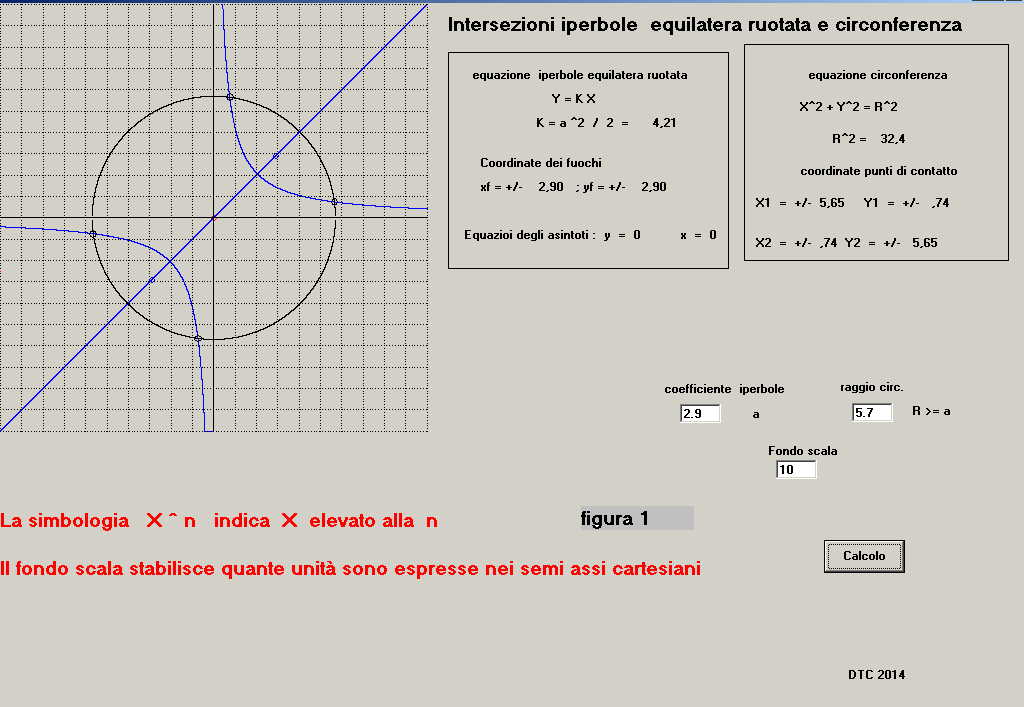
In figura 1 vediamo:
-i due rami dell'iperbole, il loro asse e i due fuochi tracciati in blu
-la circonferenza con centro nell'origine degli assi tracciata in nero
-i 4 punti di contatto tra le coniche tracciati in nero
- i dati relativi alle coordinate dei fuochi: xf = +/- 2.90 ; yf = +/- 2.9
-i dati relativi alle coordinate dei punti di contatto tra le coniche:
x1 = +/- 5.65; y1 = +/- 0.74
x2 = +/- 0.74; y2 = +/- 5.65

Secondo esercizio per R = a: ( R = 0.7 ; a = 0.7 ) e fondo scala = 10:
L'esercizio, mostrato in figura 2a, computati:
k = 0.7² / 2 = 0.245
R² = 0.7² = 0.49
presenta la soluzione del sistema:

Y = +/- 0.245 / X
X² + Y² = 0.49



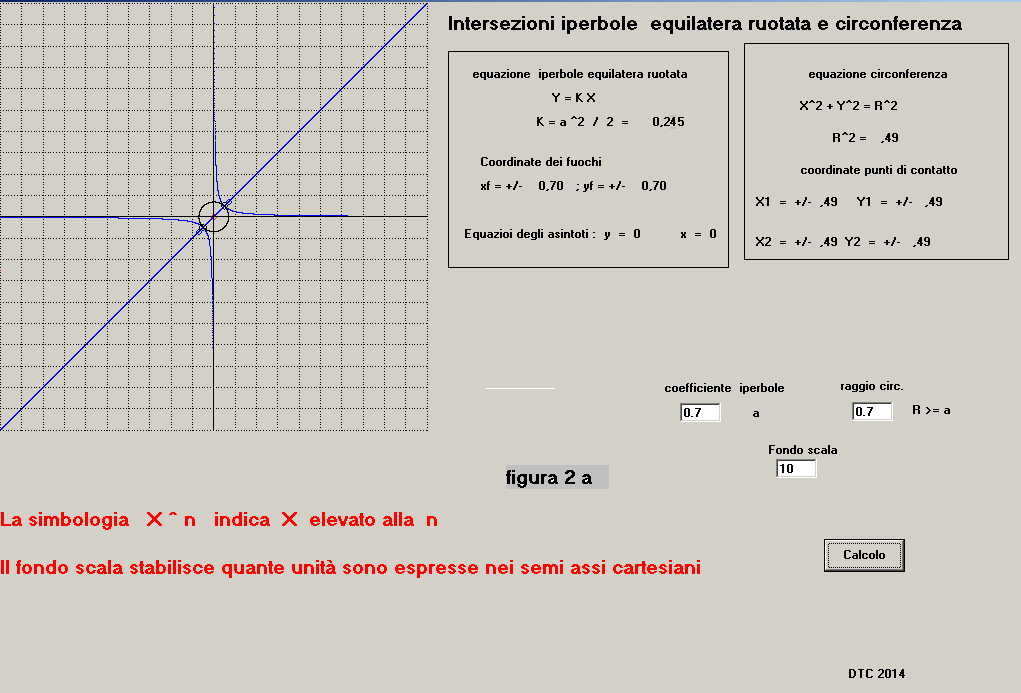
In figura 2a vediamo:
-i due rami dell'iperbole, il loro asse e i due fuochi tracciati in blu
-la circonferenza con centro nell'origine degli assi tracciata in nero
-i 2 punti di contatto tra le coniche tracciati in nero (le curve sono ora tangenti)
- i dati relativi alle coordinate dei fuochi: xf = +/- 0.7 ; yf = +/- 0.7
-i dati relativi alle coordinate dei punti di contatto tra le coniche sono ora coincidenti:
x1 = +/- 0.49; y1 = +/- 0.49
x2 = +/- 0.49; y2 = +/- 0.49
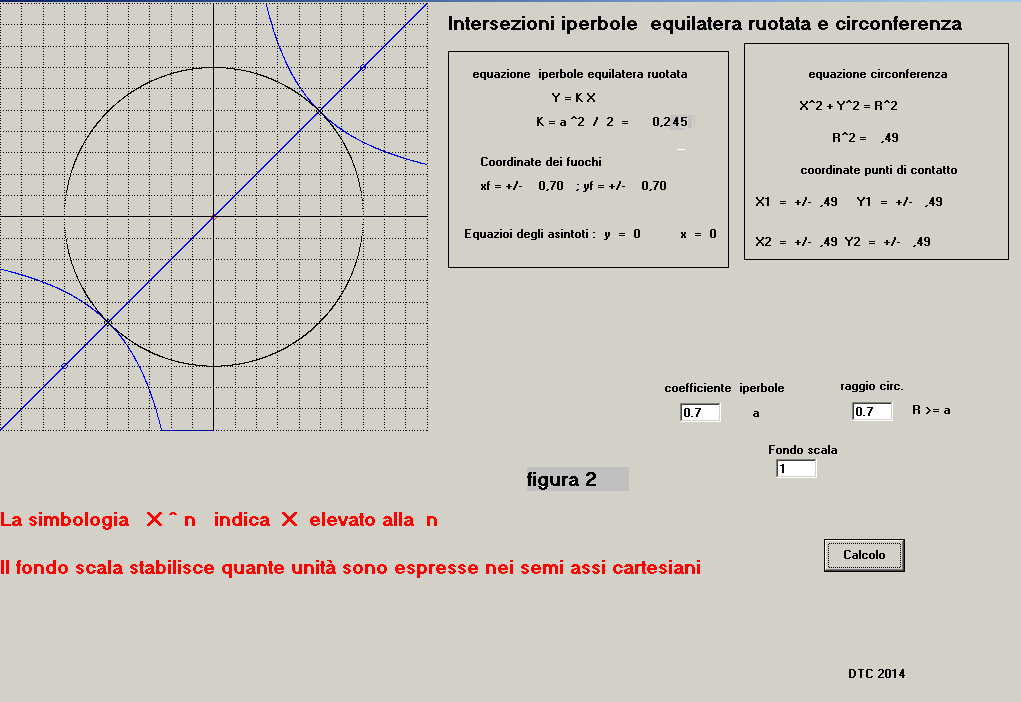
Si osserva che, dati i piccoli valori di "a" ed "R" , il grafico presenta una scarsa visibilità; se si ripete il calcolo con un valore di fondo scala diverso da 10, ad esempio fs = 1, si ottiene un grafico più ampio così come mostra la figura 2:



Terzo esercizio per R < a: ( R = 3.5 ; a = 4.7 ) e fondo scala = 10:
L'esercizio, mostrato in figura 3, computati:
k = 4.7² / 2 = 11.04
R² = 3.5² = 12.25
verifica l'impossibilità della soluzione del sistema:

Y = +/- 11.04 / X
X² + Y² = 12.25



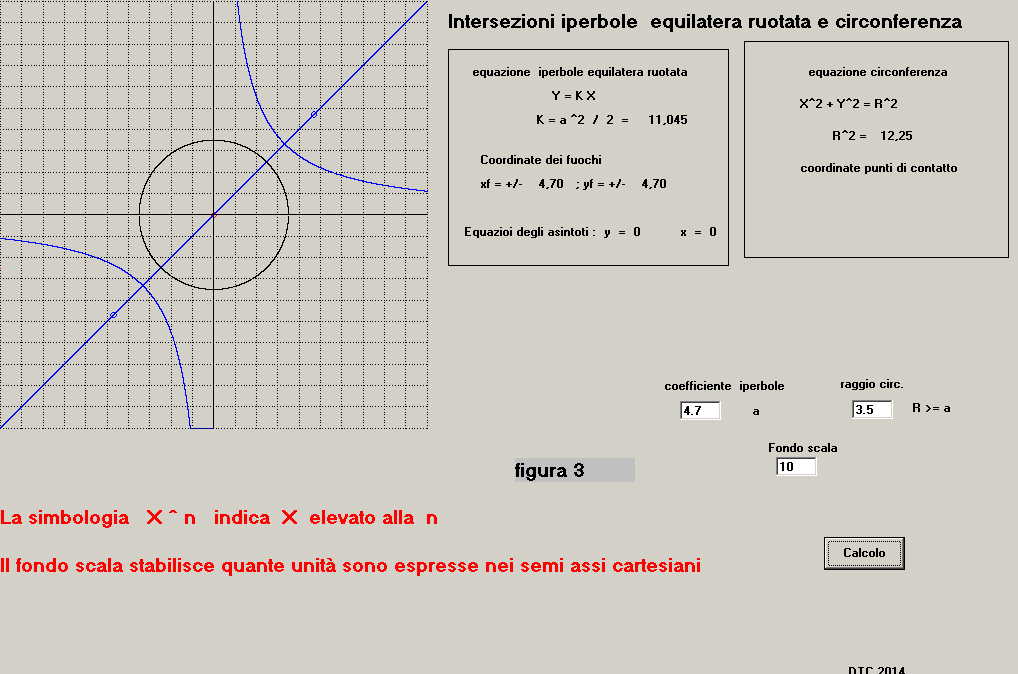
In figura 3 vediamo:
-i due rami dell'iperbole, il loro asse e i due fuochi tracciati in blu
-la circonferenza con centro nell'origine degli assi tracciata in nero
-nessun punto di contatto tra le coniche essendo R < a il sistema non ammette soluzioni
-i dati relativi alle coordinate dei fuochi: xf = +/- 4.7 ; yf = +/- 4.7
-sono assenti i dati relativi alle coordinate dei punti di contatto tra le coniche

4)Note
-Il controllo software del file eseguibile è stato eseguito al meglio; è possibile però che qualche particolare anomalia sia sfuggita all'esame.
Si prega pertanto chi dovesse riscontrare qualche difetto nell'impiego del programma di renderlo noto tramite " Contatti con l'autore"; si provvederà all'aggiustaggio in rete.