1) Generalità
Visto l'interesse per la struttura del sonar FALCON, illustrata alla pagina p4, ritengo opportuno chiarire le differenze sostanziali tra la matrice di correlazione di cui allo studio originale e le matrici operative sviluppate nella realizzazione del prototipo.
Si dimostra come, complicando un poco il software, si riduca notevolmente l'hardware di processo del sonar.
Le routine di calcolo alle quali si farà cenno in questa pagina sono scritte in linguaggio VB.

2) Lo studio originale del sonar FALCON
Lo studio del sonar FALCON, pubblicato a cura dell'Arsenale M.M. di La Spezia, è stato riportato in formato pdf nella pagina p4 di questo sito assieme ad un file ppt che illustra le motivazioni che hanno dato vita a questo progetto.
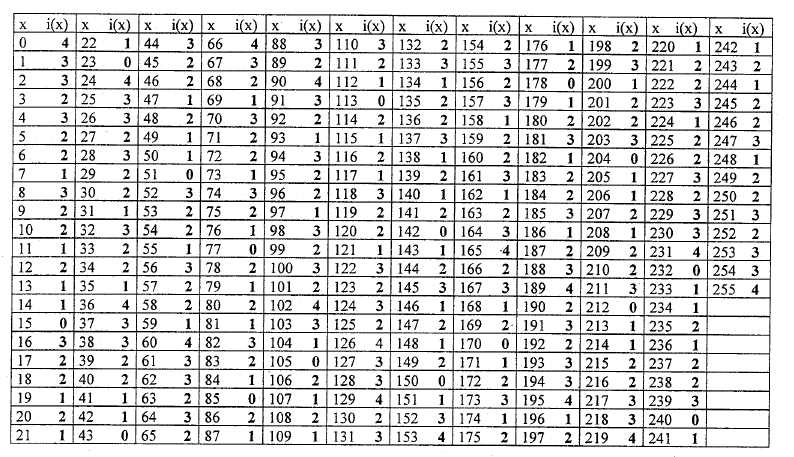
La filosofia FALCON si basa, come visto a pagina 11 del pdf citato, su processi di correlazione dipendenti da una tabella di conversione a 8 bit riportata nel paragrfo 10) della presente pagina.
Questa struttura di principio prevede l'ingresso al P.C. (facente parte del sonar FALCON), tramite tante operazioni i di "INPUT" quanti sono i fasci acustici da realizzare; nel nostro caso i fasci sono 36.
Una operazione di questo tipo richiede un multiplexer hardware in grado di selezionare, a comando sincrono da P.C. 36 gruppi di segnali diversi a 8 bit; un gruppo di segnali per ogni fascio direttivo programmato (ciascun gruppo è formato dalle tensioni idrofoniche della base acustica opportunamente amplificate, filtrate, limitate in ampiezza a due stati così come illustrato nella relazione di progetto.)
La figura 1 mostra il criterio di selezione dei 36 fasci che sarebbe stato necessario secondo l'impostazione originale di principio.



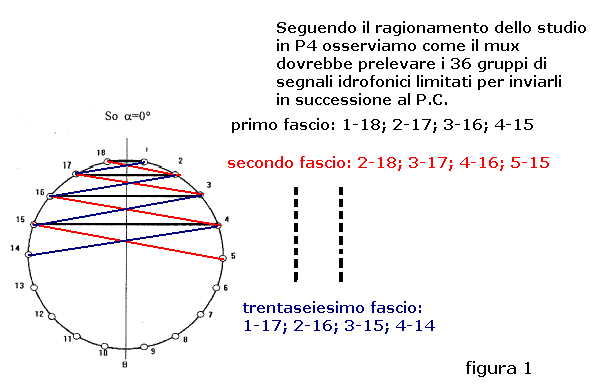
Infatti ciascuno dei 36 gruppi di segnali applicati al P.C. sarebbe stato posto all'ingresso della matrice di conversione a 8 bit per estrarne immediatamente il grado di correlazione complessivo tra i quattro gruppi di segnali, quindi il processo d'integrazione numerica ecc.
Secondo questa procedura la selezione idrofoni per la formazione dei 36 fasci sarebbe affidata esclusivamente all'hardware esterno.
Questo tipo d'acquisizione fasci da parte del P.C. richiede sia un pesante hardware relativo al multiplexer sia un notevole impegno del tempo di elaborazione dati.
Il problema è stato risolto attraverso lo studio di particolari tabelle di conversione a 16 bit che richiedono soltanto 3 operazioni di input invece che 36!!! di questo si tratta nei paragrafi seguenti.

3) La selezione idrofoni nel FALCON operativo
Per la descrizione di questo paragrafo sarà fatto riferimento ad una base circolare di 36 idrofoni della quale sono utilizzati soltanto quelli a numero dispari; si tratta quindi sempre di una struttura come quella di figura 1 ma rispondente alla situazione reale che si trovava sui smgg Toti e Sauro.
Le matrici di correlazione nel FALCON operativo sono costruite con lo stesso criterio della matrice illustrata a pagina 14 di p4 ma, ad eccezione di una, lavorano su 16 bit invece che su 8 secondo la seguente modalità di invio segnali al P.C.
Con questa procedura la selezione degli idrofoni per la formazione dei fasci è affidata completamente al software.
L'introduzione dei segnali nel P.C. viene svolta con 3 input (tre stringhe binarie) secondo quanto illustrato in figura 2:

figura 2

La sequenza dei 3 input è individuabile in figura 2 secondo le lettere: X1; X2; X3 che introducono rispettivamente i segnali idrofonici limitati degli idrofoni:
X1 = 11; 13; 15; 17; 19; 21; 23; 25.
X2 = 27; 29; 31; 33; 35; 1; 3; 5.
X3 = 7; 9; 11; 13; 15; 17; 19; 21
Ad esempio una stringa Xn qualsiasi espressa in numero binario potrebbe, ad un certo istante, essere:
Xn = 00101101
In figura, con tratto rosso (i1... i36), sono indicate le direzioni dei 36 fasci preformati che saranno realizzati con le matrici FALCON, metà fasci sono centrati sulle posizioni degli idrofoni dispari, altri fasci sono centrati sulle posizioni degli idrofoni pari non utilizzati per la formazione fasci.
Si può notare come alcuni idrofoni siano inseriti per una seconda volta da X3 ; la ragione sta nel fatto che il terzo input dedicato soltanto a 2 idrofoni, può inserirne altri 6, già presenti in posizioni diverse, ciò per alleggerire sensibilmente il software per la formazione dei fasci.
Dato che le stringhe a 8 bit, X1; X2; X3; individuano, disgiunte, rispettivamente le direzioni:
175°; 335°; 135°; per ciascuna di queste la matrice di correlazione è ancora l'originale a 8 bit.

4) La composizione delle stringhe e delle matrici da 16 bit
Con l'ingresso nel P.C. delle tre stringhe X1; X2; X3, queste devono essere collegate tra loro per trasformarle in stringhe a 16 bit necessarie per interrogare le matrici di correlazione del sonar operativo.
Sulla base dell'impostazioni delle matrici a 16 bit la sequenza dei 3 input collegati deve essere:
X1 con X2
X2 con X3
X3 con X1
Secondo la seguente impostazione logica:
z = X1 Or (255 * X2)
z1 = X2 Or (255 * X3)
z3 = (((X3 And 2) / 2) Or (2 * X1)) And 255
z4 = (X3 And 3) Or (4 * X1)

Questa impostazione è la migliore per ridurre al minimo il numero delle matrici di correlazione.
E' opportuno ricordare che le matrici a 16 bit di cui si parla rendono 5 livelli del coefficiente di correlazione quali 0; 1; 2; 3; 4 così come le matrici originali a 8 bit descritte in p4.
Il numero di 16 bit delle attuali matrici è necessario soltanto per la formazione software dei 36 fasci preformati e non per aumentare i livelli di correlazione.
Dal punto di vista dei controlli del software intesi a stabilire la corretta costruzione delle matrici, cosa è la matrice a 8 bit, facilmente tabulabile, e quindi verificabile, come indicato a pagina 14 dello studio citato in precedenza, cosa è il controllo di una tabella con ben 2^16 locazioni = 65536 quali sono quelle del presente paragrafo; questo problema sarà affrontato in altra pagina del sito.
Le matrici di correlazione sono caricate sul P.C. una sola volta all'accensione del sonar, la carica richiede diversi secondi in base alla velocità del processore.

5) Criteri per la composizione delle matrici da 16 bit
Spiegare come si compone una delle matrici a 16 bit presenta alcune difficoltà, ci si deve aiutare sia con il listato del programma che con la grafica che vede il fascio da formare nell'ambito del disegno della base acustica.
Il programma in VB che consente la scrittura in memoria di una delle diverse matrici di correlazione a 16 bit del tipo illustrato nel paragrafo 4) si sviluppa secondo la routine:

For X = 0 To 65536
Y1 = X And 15
Y2 = X And 480
Y3 = Int(Y2 / 32)
Y4 = Int((Y3 And 1) * 8) + Int((Y3 And 2) * 2) + Int((Y3 And 4) / 2) + Int((Y3 And 8) / 8)
Y5 = Abs((Y1 Xor Y4) - 15)
Y6 = (Y5 And 1) + ((Y5 And 2) / 2) + ((Y5 And 4) / 4) + ((Y5 And 8) / 8)
Ic2(X) = Y6
Next X

Le righe di questo programma si riferiscono alla costruzione della matrice di correlazione per la generazione del fascio Ic2 relativo alla direzione 185° rispetto all'asse del battello.
Una qualsiasi matrice relativa a fasci preformati indirizzati su altre direzioni può essere descritta in modo simile.
Individuiamo ora il fascio a 185° tracciato sulla base acustica di figura 3



al fascio concorrono gli idrofoni uniti dai segmenti tracciati in rosso:
i livelli logici ( 1 o 0 ) dei segnali idrofonici limitati, generati della base idrofonica di figura 3, individuati da X1 e da X2 sono nominati con lettere: an; bn; Ko-K7; come segue:

k1 .. k7 = serie livelli logici degli idrofoni 5; 3; 1; 35; 33; 31; 29 non interessati al fascio
b4 = livello logico idrof. 27
b3 = livello logico idrof. 25
b2= livello logico idrof. 23
b1 = livello logico idrof. 21
ko = livello logico idrof. 19 non interessato al fascio
a4 = livello logico idrof. 17
a3 = livello logico idrof. 15
a2 = livello logico idrof. 13
a1= livello logico idrof. 11

In questo caso la stringa a 16 bit è composta da X1 e X2 secondo la sequenza:

Z = k7 - k6 - k5- k4 - k3 - k2 - k1 - b4 - b3 - b2 - b1 - ko - a4 - a3 - a2 - a1

La massima correlazione tra le 4 coppie di segnali si avrà quando, ad ogni istante e sempre nel tempo, i segni di ciascuna delle 4 coppie saranno uguali tra loro come ad esempio:
a4 = 0; b1 = 0
a3 = 1; b2 = 1
a2 = 0; b3 = 0
a1 = 1; b4 = 1
In tal caso il valore di correlazione sarà pari a C = 4.
Quando non tutte le 4 coppie avranno segni identici il valore di correlazione assumerà valori variabili come:
C = 3; C = 2; C = 1; in funzione del grado di correlazione esistente.
Se ad ogni istante e per sempre nel tempo ciascuna delle 4 coppie di segnali avrà segni opposti si avrà C = 0: questa condizione è detta di "inversocorrelazione".
La matrice, per essere interrogata da una stringa del tipo menzionato, si compone secondo i seguenti passi logici dove il primo (For X = 0 To 65536) varia l'indirizzo della matrice associando ad esso, come contenuto delle cellule della matrice, il numero delle coincidenze dei segni presenti rispetto al centro della stringa dei soli 9 bit msb del numero stesso; sono quindi trascurate tutte le eventuali coincidenze tra i segni dei bit oltre il nono:

1) con For X = 0 To 65536: indirizza successivamente tute le memorie Ic2(x) per caricare i dati
2) con Y1 = X And 15: s'isolano i 4 bit inferiori in Y1 = a4 - a3 - a2 - a1
3) con Y2 = X And 480: si forma la stringa Y2 = b4 - b3 - b2 - b1 - k - k - k - k - k
4) con Y3 = Int(Y2 / 32): si eliminano le posizioni in k e si crea la stringa Y3 = b4 - b3 - b2 - b1
5) con Y4 = Int((Y3 And 1) * 8) + Int((Y3 And 2) * 2) + Int((Y3 And 4) / 2) + Int((Y3 And 8) / 8):
si capovolge Y3: Y4 = b1 - b2 - b3 - b4
6) con Y5 = Abs((Y1 Xor Y4) - 15): si esegue la moltiplicazione dei segni tra Y1 e Y4 (correlazione)
7) con Y6 = (Y5 And 1) + ((Y5 And 2) / 2) + ((Y5 And 4) / 4) + ((Y5 And 8) / 8):
si esegue la somma delle coincidenze di correlazione calcolate con Y5
8) con Ic2(X) = Y6: si pone nella memoria Ic2 il valore di correlazione relativo alla somma delle 4 coppie di segnali.
9) con Next x: rimanda alla prima riga della routine

In questo modo una volta lanciata la routine la memoria Ic2 conterrà 65536 locazioni e soltanto quelle relative all'impostazione data forniranno i coefficienti di correlazione delle 4 coppie dei segnali.

6) Caratteristiche numeriche della matrice Ic2 per 185°
Nella composizione della matrice Ic2 la variabile X si estende da X=0 a X=65536 caricando in Ic2 i valori di correlazione relativi ai valori di X stesso (da C = 0 a C = 4)
Per la direzione 185°, così come per tutte le altre, le combinazioni dei segni delle 4 coppie di segnali che indicano piena correlazione (C=4) possono essere ad esempio:

b1 = 0
b2 =1
b3 =0
b4 =0
ko = idrofono non interessato al fascio
a4 = 0
a3 = 1
a2 = 0
a1 = 0

La serie di tutte le 32 combinazioni possibili per la direzione 185° è riportata, in dettaglio, nel paragrafo 9.
Dal citato paragrafo si evince che le 32 locazioni legate alla direzione 185°, interrogate, daranno sempre C = 4 dato che le 4 coppie dei segnali che indirizzano la matrice sono sempre coerenti nel tempo assunto che il segnale del bersaglio sia da considerarsi persistente.

7) Esempio d'impiego delle matrici da 16 bit
Un esempio d'impiego della routine di paragrafo 5 aiuterà a comprendere meglio la procedura di composizione del fascio preformato per 185°.
Supponiamo che il bersaglio sia centrato sulla direzione di 185° e che il segnale ricevuto da esso sia privo di rumore, in questo caso, per un certo istante, la correlazione tra le quattro coppie d'idrofoni sarà massima con i segnali logici su an; bn; come ad esempio :
b1 = 1
b2 =1
b3 =0
b4 =1
ko = idrofono non interessato al fascio
a4 = 1
a3 = 1
a2 = 0
a1= 1
Con questi livelli logici la stringa a 16 bit formata con X1 e X2 sarà:

Z = k7 - k6 - k5 - k4 - k3 - k2 - k1 - 1 - 0 - 1 - 1 - ko - 1 - 1 - 0 - 1

questa è la stringa che interroga la matrice di correlazione per la direzione 185° ; la risposta della matrice è indipendente dai valori casuali ( 1; 0 ) dei bit in kn.
Per chiarire il concetto esaminiamo il numero decimale rappresentato da z, si possono presentare diversi casi da controllare facendo girare la routine esposta nel paragrafo 5:
Per ko = 0 e K1_K7 = 0; z = 365 si ha: C = 4
Per ko = 1 e K1_k7 = 0; z = 381 si ha: C = 4
Ciò significa che qualsiasi livello di Ko ( 0 or 1 ) non impedisce alla matrice di rilevare il livello di massima correlazione esistente tra le quattro coppie di segnali presenti nella stringa a 16 bit.
Ciò si verifica e si può ripetere per:
ko = 0 e K1_K7 = ( 0; 2^9 ... 2^16) casuali; z = 365 + (2^9 _ 2^16) casuale si ha sempre: C = 4

8) In chiusura

Nella composizione delle matrici a 16 bit non sempre si utilizzano le 65536 locazioni di memoria, volendo si potrebbero ridurre adattandole, fascio per fascio, per rendere più rapido il caricamento all'avvio del sistema; questa procedura sarebbe pagata da un moltiplicarsi delle variabili z; z1; z2; z3; z4 a scapito delle velocità di calcolo durante l'impiego del FALCON.

Nel testo è presente soltanto la routine per la composizione della matrice relativa al fascio di 185°; questa può essere copiata in programmi in VB per prove e controlli.
Per le routine delle matrici relative agli altri fasci se ne può fare richiesta tramite la pagina del sito "Contatti" ; saranno inviate gratuitamente all'indirizzo email indicato dal richiedente.

9) Dettagli sulla tabella di correlazione Ic2

I dettagli mostrano quali sono i numeri Y, che interrogando la matrice Ic2, rendono il massimo coefficiente di correlazione: C = 4
Nella tabella sottostante a fianco di ciascun numero è rappresentata la stringa binaria che gira sul P.C. per le 32 locazioni relative alla direzione 185°.
Y = 0 bin = 000000000 C = 4
Y = 16 bin = 000010000 C = 4
Y = 40 bin = 000101000 C = 4
Y = 56 bin = 000111000 C = 4
Y = 68 bin = 001000100 C = 4
Y = 84 bin = 001010100 C = 4
Y= 108 bin = 001101100 C = 4
Y= 124 bin = 001111100 C = 4
Y= 130 bin = 010000010 C = 4
Y= 146 bin = 010010010 C = 4
Y= 170 bin = 010101010 C = 4
Y= 186 bin = 010111010 C = 4
Y= 198 bin = 011000110 C = 4
Y= 214 bin = 011010110 C = 4
Y= 238 bin = 011101110 C = 4
Y= 254 bin = 011111110 C = 4
Y= 257 bin = 100000001 C = 4
Y= 273 bin = 100010001 C = 4
Y= 297 bin = 100101001 C = 4
Y= 313 bin =100111001 C = 4
Y= 325 bin = 101000101 C = 4
Y= 341 bin = 101010101 C = 4
Y= 365 bin = 101101101 C = 4
Y= 381 bin = 101111101 C = 4
Y= 387 bin = 110000011 C = 4
Y= 403 bin = 110010011 C = 4
Y= 427 bin = 110101011 C = 4
Y= 443 bin = 110111011 C = 4
Y= 455 bin = 111000111 C = 4
Y= 471 bin = 111010111 C = 4
Y = 495 bin = 111101111 C = 4
Y = 511 bin = 111111111 C = 4

10) La tabella di correlazione originale a 8 bit (C. Del Turco)