1) Generalità
Lo studio di sistema del sonar si estende naturalmente verso la struttura a fasci preformati con l'esame delle caratteristiche di direttività della base ricevente.
Dalla base acustica dipendono sia l'errore massimo di puntamento sia la risoluzione angolare.
Per entrambe le variabili si farà riferimento a pagine dedicate di questo sito.
Ricordiamo che i livelli dei segnali acustici saranno espressi in dB/μPa/√Hz , le tensioni in dB/V/√Hz, i dati elaborati dai calcolatori come rapporti tra segnali e disturbi S/N(dB).
Come in precedenza il seguente paragrafo 2) riporta i dati di specifica tecnica.

2) Dati di specifica tecnica
Di seguito sono riportate le voci delle diverse caratteristiche volute dall'utilizzatore:

A)- Tipo base ricevente : conforme allo scafo del battello ( zona a proravia compresa in un
settore di +/- 160° )- limitandone al massimo le dimensioni e il peso -.

B)-Portata di scoperta minima al traverso: R = 55 Km alle condizioni:
Propagazione sferica
Bersaglio CT a 15 nodi
Stato del mare SS = 2
Condizioni probabilistiche: Priv = 90 % Pfa = 5 %
Unico grado di libertà: "DI" guadagno di metà base conforme al traverso

C)- Banda delle frequenze di ricezione : 200 Hz - 3500 Hz

D)- Rumore dei preamplificatori Ne < mare forza zero (SS=0)

E)- Scoperta a fasci preformati : in un settore di +/- 160° rispetto all'asse del battello

F)- Processo dei segnali: in correlazione

G)- Costante di tempo d'integrazione: RC = 1 Sec.

H)- Dinamica per CT a 15 nodi da 100 m a 55 Km

I)- Errore strumentale massimo di rilevamento al traverso : Δα = 1°

L)- Risoluzione angolare al traverso: Δφ = 5°

M)- Presentazione video a cascata in BRQ (storia 30 Sec) con indice di collimazione man. e aut.

3)Determinazione del numero dei fasci preformati E); I) s.t.
In aderenza ai punti E) ed I) delle specifiche tecniche si esamina la struttura dei fasci preformati che devono coprire l'arco di ricezione del sonar tra -160° e + 160° rispetto all'asse del battello.
Lo studio del fasci preformati prevede il calcolo delle caratteristiche di direttività della base per diverse direzioni da stabilire; tra queste le direzioni al traverso che, utilizzando l'estensione maggiore della base, presentano le migliori caratteristiche di scoperta e di precisione.
Vediamo quindi come calcolare le direttività al traverso di uno tra i fasci preformati che, secondo il punto F) delle specifiche tecniche, devono essere in correlazione.

4) Calcolo delle curve di direttività al traverso
Se consideriamo la base acustica al traverso secondo la nota figura 3 di p146 che riportiamo in figura 1:

figura 1

possiamo calcolare la direttività della base rettilinea "rossa" secondo la classica funzione sviluppata da Stenzel relativa a segnali in banda di frequenze ( si veda p39 ):



I nostri dati sono :
n = 14 (quattordici stecche disposte alla distanza di λ/2 l'una dall'altra)
L = ( 14 - 1 ) * λ/2 = 13 * 0.827/2 = 5.37 m
f1 = 200 Hz
f2 = 3500 Hz
Con i dati esposti si calcola la curva di direttività riportata in figura 2:



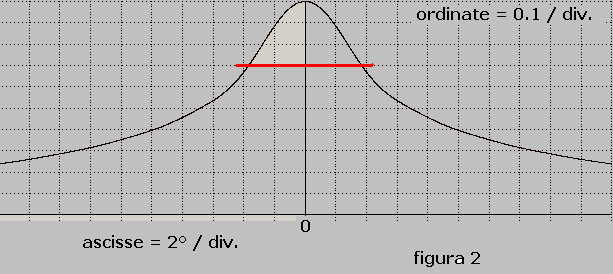
La figura mostra che la larghezza 2β del lobo a - 3 dB, segmento rosso, è di circa 8°.
La curva in oggetto rappresenta la direttività di una base acustica quando le 14 tensioni idrofoniche sono sommate tra loro in banda 200-3500 Hz; non è affatto la risposta in correlazione così come indicato al punto F) della specifica tecnica.
Dato che, secondo teoria, la curva di direttività in correlazione ha un lobo di larghezza metà rispetto a quello della curva di figura 2, questa sarà pari a 2β = 4°, come mostra la figura 3:



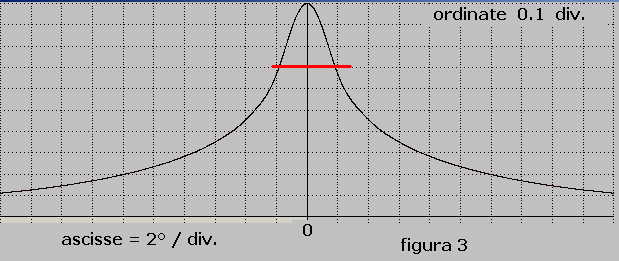
E' sulla scorta del valore di 2β che definisce la larghezza del lobo del primo fascio preformato in correlazione, al traverso, che saranno sviluppati i calcoli per la determinazione del loro numero.

5) Calcolo del numero dei fasci preformati
In generale la funzione che consente il calcolo del numero dei fasci preformati, partendo dalle dimensioni della caratteristica di direttività (si legga larghezza del lobo) e dall'errore accettato a seguito della campionatura spaziale (si legga errore massimo strumentale), si evince dalla teoria dimostrata in p3.
Nel caso in oggetto, relativo ad una base lineare, è più perspicuo il calcolo della distanza angolare tra fasci adiacenti che non il loro numero; questa distanza, sempre nel rispetto del criterio di campionatura e dell'errore accettato porta all'algoritmo:



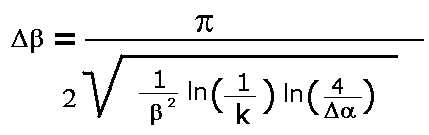
dove:_
Δβ = intervallo angolare tra due fasci preformati (zona del traverso)
β = semilarghezza del lobo di direttività al traverso
ln ( ) = logaritmi neperiani
K = ampiezza del lobo di direttività per l'angolo β
Δα = errore massimo strumemtale

Da figura 3 e da I)s.t. abbiamo:
β = 2°
K = 0.7
Δα = 1° :
Con questi valori il calcolo mostra che l'intervallo angolare tra due fasci preformati nella zona del traverso è: Δβ = 4.46°; arrotondabile a Δβ = 5°.
Se s'immagina un fascio preformato a 0° sull'asse del battello e gli altri distribuiti a sinistra e a destra
sui + / - 160° il numero complessivo dei fasci risulta:
N = (2 * 160° / 5°) + 1 = 65.
Dato che la larghezza dei lobi di direttività 2β aumenta a mano a mano che ci si scosta dalla direzione al traverso la campionatura dello spazio, di un fascio ogni 5°, per direzioni verso prua o verso poppa diventa eccessiva; ciò non pregiudica però il corretto funzionamento del sonar.

6)Osservazioni a chiusura della pagina
A seguito di quanto detto alla fine del precedente paragrafo emerge che la distribuzione dei fasci preformati è ridondante, quindi inutile; l'alternativa sarebbe di dividere l'arco di +/- 160° in settori a diverso intervallo tra i fasci.
Questo tipo di soluzione con intervallo di campionatura variabile a settori pone un serio problema al software di elaborazione quindi, secondo lo scrivente, è più facile accettare il sovra campionamento che nasce dai calcoli sopra esposti che non appesantire le routine di calcolo dato che azioni in tal senso non porterebbero nessun vantaggio funzionale.