L'integrale di Debye
(2° della serie degli integrali particolari)

-Calcolo automatico del valore numerico tra i limiti d'integrazione per gli integrali definiti-

1) Generalità
Con questa pagina si apre la 2^ di una serie di routine per il calcolo degli integrali definiti a carattere particolare: l'integrale di Debye.
Le tabelle dell'integrale, calcolato in funzione del limite d'integrazione superiore "X" e dell'esponente "n" si trovano con passi di X = 0.1, con questo lavoro si possono calcolare i valori di I(X) anche per intervalli inferiori.

2) L'integrale Debye
La forma analitica dell'integrale in oggetto è sotto riportata:



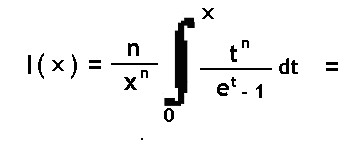
dove l'estremo superiore d'integrazione, "X" , si estende da 0 a 10, l'esponente "n" con interi da 1 a 4; entrambi i valori sono impostati dall'utilizzatore: nell'apposito Text Box per " X = ", e dal Combo per "n" come mostra il pannello operativo di figura 1:

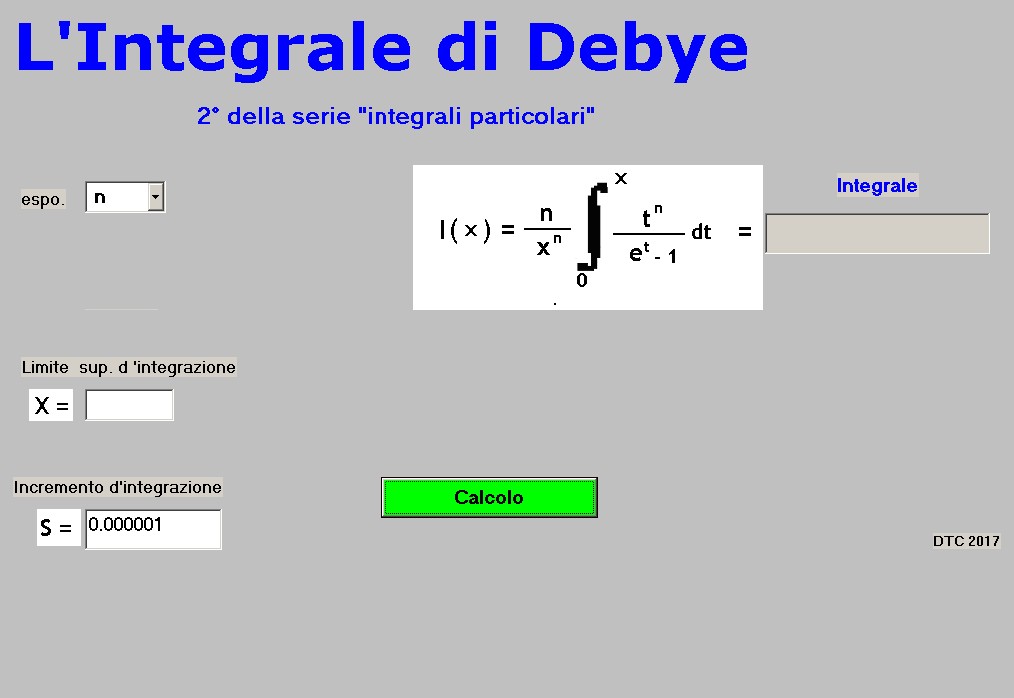figura 1

Come si vede in figura un secondo Text Box, S, sotto il primo, consente di stabilire l'incremento del processo d'integrazione fissato; il valore S sostituisce l'infinitesimo "dt" nel processo di calcolo di I(X).
Al lancio del programma "S" è fissato a: S = 0.000001; questo è un incremento medio che consente calcoli veloci con precisioni fino a sei decimali.
Il pulsante "Calcolo" a riposo è di colore verde, una volta premuto permane di colore rosso per tutto il tempo di calcolo; è un modo per giustificare il tempo d'attesa per lo sviluppo del processo.

3) Esempi di calcolo
Il calcolo dell'integrale si esegue chiamando l'eseguibile in VB6: IP2.exe che presenta la schermata di figura 1 .

I risultati degli esempi si confrontano con un dato tabellare preciso a 6 decimali:
a caso un valore calcolato per X = 5 ed n = 3
il valore dell'integrale é: I(X)= 0.117597.

-primo esempio:
per S impostato in automatico al lancio del programma: S = 0.000001
e per X = 5 ed n = 3 si ha: I(X)= 0.117597 coincidente con il valore di tabella. .

-secondo esempio:
Supponiamo che per velocizzare il calcolo s'imposti manualmente S: S = 0.001; per X = 5 ed n = 3 si ha: I(X)= 0.117587
con errore di 1/100000 rispetto al calcolo precedente.

Home

Stampa immagine grafica o descrizione testuale