Sulle applicazioni della legge di Snell in acustica subacquea

1) Generalità

Tutte le pagine del sito che trattano della propagazione anomala del suono in mare, si vedano p24; p26; p28; p30; p162, hanno alla base, anche se non espressamente menzionata, la legge di Snell.
Questa legge definisce il comportamento di un raggio acustico quando, nel suo percorso in mare, attraversa due zone a diversa temperatura (t1; t2) nelle quali anche la velocità del suono assume due diversi valori (C1; C2).
In questa pagina esamineremo a fondo, per via matematica, la legge di Snell e le sue applicazioni.

2) La relazione tra temperatura dell'acqua e la velocità del suono

Prima di proseguire nello sviluppo di questa pagina è utile evidenziare come, in base ai rilievi della temperatura in mare, si possa calcolare la velocità del suono.
La relazione tra "C" in m/sec e "t" in gradi centigradi" è data da diverse formule empiriche, la formula più impiegata, dovuta a modificazioni dell'originale di Wilson, è:

C = 1410 + 4.21 t - 0.037 t² + 1.1 S + 0,018 z    1)

dove:
C = velocità de propagazione del suono espressa in metri/Secondo
t = temperatura dell'acqua in °C
S = salinità in parti/1000
z = profondità zona di calcolo

In superficie per t = 13°, salinità del 35 parti per mille, z = 1m, il valore di C è pari a circa 1500 m/Sec, questa è la velocità del suono che generalmente viene messa a calcolo nelle computazioni relative al sonar eccezion fatta per i calcoli sulla propagazione anomala nei quali C è variabile.
Nella 1) il valore della temperatura "t" può essere computato in funzione della profondità "z" una volta che sia noto il gradiente di temperatura "g" scrivendo:
t = k + g z
dove:
K = temperatura nel punto di generazione del suono ( ad esempio k = 10°)
g = gradiente di temperatura ( ad esempio - 0.1 C°/ metro)
z = profondità in metri

Un esempio grafico del calcolo della 1) in funzione della profondità, con sorgente acustica in superficie, è riportato in figura 1 per i seguenti valori:
-profondità "z" variabile da 0 a 200 m.
-temperatura in superficie K = 20 c°
-gradiente di temperatura g = -0.1 c° / m (gradiente negativo)
-salinità = 35
-scala delle ascisse (profondità) da z = 0 a z = 200 m divisa in 20 intervalli da 20 m/ div.
-scala dele ordinate (velocità del suono C = f(z)) da 1400 m/Sec. a 1500 m/Sec. divisa in 10 intervalli da 10 m/Sec / div.

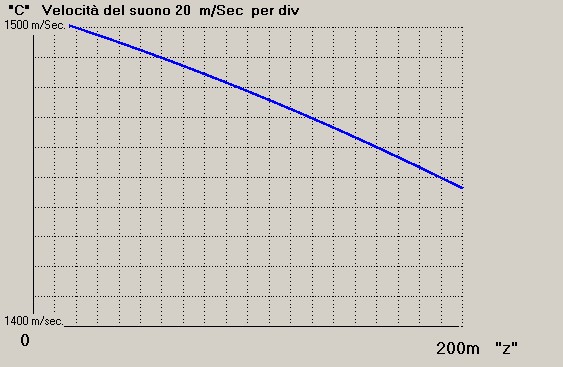figura 1

Dalla curva si osserva che la variazione della velocità del suono è percentualmente molto piccola ( dell'ordine dello 0.34 % ), ciò nonostante questa provoca tutte le problematiche relative alla propagazione anomala.
Il diagramma di figura 1 è costruito secondo le regole classiche della geometria analitica che pone in ascisse la variabile indipendente (nel nostro caso la profondità "z") ed in ordinate la variabile dipendente ( in figura 1 la velocità C del suono ).
Al fine di rendere più aderente alla realtà ambientale del problema la curva di figura 1 è generalmente tracciata con l'asse della profondità in senso verticale, facendo così coincidere la superficie del mare
( "z" = 0 ) in alto e verso il basso i valori crescenti di profondità, in queste condizioni la variabile dipendente "C" si trova in alto così come mostra figura 2:

figura 2

A seguito del gradiente negativo della temperatura il grafico è inclinato verso l'asse "z", gradienti di temperatura popsitivi inclinerebbero la curva dal lato opposto.
La velocità di propagazione del suono, in funzione della profondità, è rilevabile direttamente, senza misure di temperatura da un dispositivo detto "bativelocigrafo"; questo strumento è impiegato esclusivamente da unità sommergibili ( si veda p85 ).
Dalla curva riportata in figura 2, la C = f(z), si può, grazie alla legge di Snell, calcolare l'andamento di un raggio acustico definito da una funzione R = f(z; δ) come mostra indicativamente la coppia di curve riportate in figura 2/a:

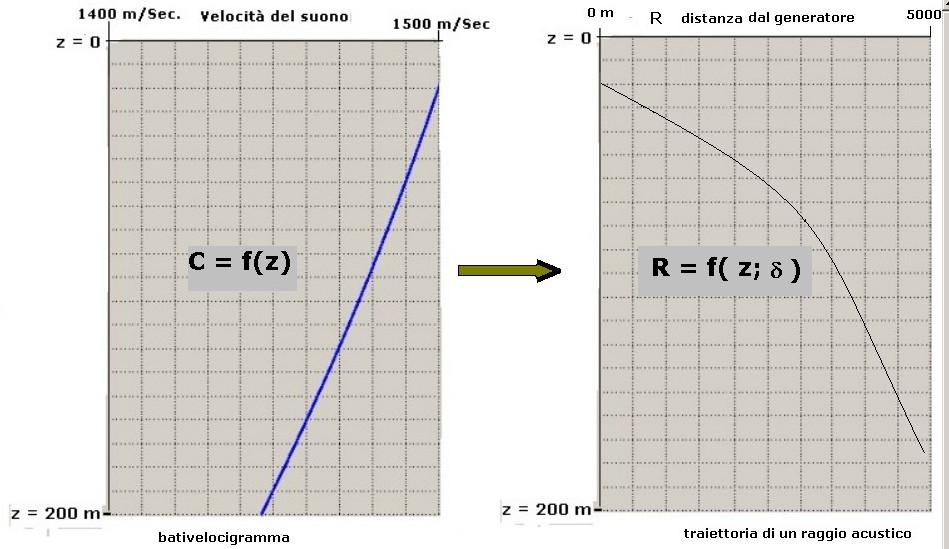figura 2a

Dalla curva di sinistra, relativa alla C = f(z) calcolata in precedenza, si traccerebbe l'andamento di un raggio acustico, mostrato nella curva a destra a solo scopo indicativo, secondo la funzione R = f(z; δ) che si estende da R = 0 a R = 5000 m in dipendenza delle variabili:
Profondità z variabile da 20 a 200 m
Angolo δ governato, come vedremo, dalla legge di Snell.

3) La legge di Snell

Per ragionare sulla legge di Snell è opportuno partire da un sistema di assi cartesiani simile a quello mostrato in figura 2 nel quale una funzione del tipo C = f(z) è presentata con due soli livelli:
C1 = 1480 m / Sec tra z = 0 e z = 100 m
C2 = 1440 m/Sec tra z = 100 m e z = 200 m
come mostra la figura 3:

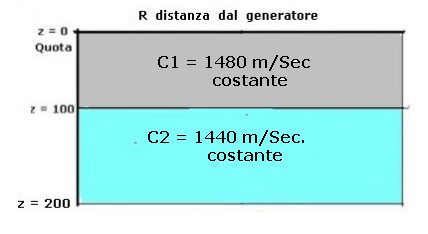figura 3

Un raggio acustico che transitasse tra le due zone di figura 3 presenterebbe l'andamento di figura 4.

figura 4

Nella zona grigia della figura 4 viene evidenziato un raggio acustico di colore celeste (raggio incidente ), nella zona celeste si evidenzia, in colore rosso, la rifrazione del primo raggio così come mostra la spezzata.
Snell definisce le variabili in figura 4 come l'uguaglianza tra due rapporti o legge della rifrazione:

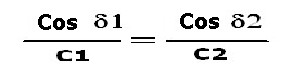2)

dalla 2), per δ1 costante si osserva:
se C2 = C1 ; δ2 = δ1
se C2 > C1 ; δ2 > δ1
se C2 < C1 ; δ2 < δ1

La relazione tra l'angolo d'incidenza δ1 e l'angolo di rifrazione δ2 è mostrata nell'equazione 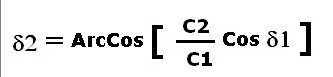3:

3)

Il grafico riportato in figura 3 mostra la variazione della traiettoria di un raggio acustico nel passaggio tra due zone ideali a temperatura diversa; in realtà, generalmente, si passerà da un valore di temperatura ad un'altro secondo una modificazione graduale della temperatura stessa e pertanto il massimo valore dell'angolo di rifrazione sarà raggiunto anch'esso gradualmente come mostra la figura 5:

figura 5

Si passa quindi dalla spezzata di figura 4 ad una curva funzione della profondità z e dell'angolo δ:

R = f(z ; δ)     4)

4) Sull'algoritmo base per il calcolo delle traiettorie dei raggi acustici

L'algoritmo per il calcolo delle traiettorie dei raggi acustici si sviluppa partendo dalla legge di Snell esposta nella 2) che riportiamo: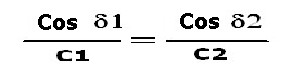

2)

Nella 1) abbiamo visto come la velocità C del suono vari con la profondità "z" generando la funzione
C = f(z) tracciata, con valori d'esempio, in figura 2; detta funzione può essere indicata, per semplicità degli sviluppi seguenti come C(z); ciò premesso possiamo riscrivere la 2) sostituendo il denominatore C2 con la funzione C(z) che rappresenta un insieme di valori che C2 stesso può assumere alle diverse profondità:

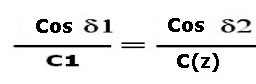4)

Sviluppando la 4) per esplicitare l'angolo δ2 scriviamo:

5)

Dato che tutti gli sviluppi teorici per il calcolo ed il tracciamento dei raggi acustici si sviluppano partendo dalla Cotangente dell'angolo δ2 vediamo come determinarla con le regole della trigonometria; posto:

Cos (x) = a

si può scrivere la seguente relazione nota:

Cot(x) = a [ ( 1 - a² ) ] ^-1/2    6)

in base alla 6) e alla 5) abbiamo infine la relazione base, la 7), per il complesso processo di calcolo generale delle traiettorie dei raggi acustuici in mare sviluppabile secondo la legge di Snell.

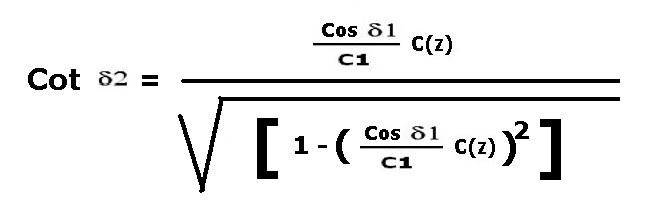: 7)




Home

Stampa immagine grafica o descrizione testuale