1) PREMESSA
Con la dizione "guadagno di direttività" ( G ) s'intende la specificazione di una delle due peculiarità relative alle basi idrofoniche che con la "caratteristica di direttività" ,studiata in p39, definiscono i dati salienti dei sistemi acustici riceventi e/o trasmittenti.
La variabile (G) è indispensabile per i calcoli della portata di scoperta di un sonar.
Il guadagno di direttività di un sistema acustico è espresso dal rapporto tra il massimo livello di segnale ricevuto e il livello del rumore ambiente captato; pù elevato è tale rapporto migliori sono le prestazioni della base.
Il guadagno di direttività è calcolabile, a seconda della tipologia delle basi acustiche, con alcune formule di relativa semplice applicabilità; la dimostrazione rigorosa delle formule è invece molto complessa e non intuitiva.
Per le ragione di cui sopra esporremmo la dimostrazione dei principi generali che governano la materia attraverso un percorso facilmente comprensibile che presuppone però l'assunto:
La distanza D tra gli idrofoni deve essere molto maggiore della lunghezza d'onda λ.

2)CONFIGURAZIONE PER L'ANALISI DEL GUADAGNO DI DIRETTIVITA'
La base idrofonica più semplice con la quale impostare un'analisi del guadagno di direttività è il dipolo, costituto, come definito dal nome, da due sensori omnidirezionali ( i1 - i2 ) così come mostrato in figura 1; in essa s'individuano la congiungente ( D ) tra i due, l'asse perpendicolare ad essa passante sulla mezzeria, due amplificatori con filtro passa basso, due interruttori k1, K2 e un circuito sommatore, a guadagno unitario.
I filtri definiscono le frequenze delle tensioni di rumore e di segnale nella banda generica compresa tra
0 e F .



Secondo la figura 1 esaminiamo tre ipotetici casi;

Caso A-Idrofoni a distanza D maggiore di 10 λ (presenza del solo rumore del mare)
Supponiamo che i due sensori siano colpiti dal solo rumore del mare e che questo generi ai capi di ciascun idrofono una tensione efficace che definiremo rispettivamente come: vn1 , vn2.
Le tensioni di rumore vn1 ed vn2, applicate ai relativi "amplificatori + filtri", siano disponibili all'uscita di questi, in banda definita, ad un livello di:
vn1' = 1 mV eff.
vn2' = 1 mV eff.
In generale, date le caratteristiche di casualità del rumore del mare nell'ambiente subacqueo, le pressioni acustiche generate sono diverse da punto a punto e colpiscono gli idrofoni del dipolo in modo che le tensioni da essi prodotte sono, ad ogni istante, diverse in ampiezza e polarità pur restando identico il loro valore efficace.

Caso B- Idrofoni coincidenti per D = 0 (presenza del solo rumore del mare)
Ipotizziamo ora, idealmente, che i due sensori siano compenetrati l'uno nell'altro, per D = 0, in tal caso i livelli di tensione generati:
vn1' = 1 mv eff.
vn2' = 1 mv eff.
essendo prodotti dalla stessa identica pressione acustica agente, negli stessi punti, avranno sempre sia ampiezza che polarità istantanee identiche.

Caso C-Idrofoni a generica distanza D (presenza del solo segnale di una sorgente acustica)
Supponiamo che i due sensori siano colpiti dal segnale di una sorgente acustica posta sull'asse del dipolo (per alfa = 0).
In questo caso, indipendentemente da qualsiasi valore D, i due idrofoni riceveranno l'onda acustica nello stesso tempo e avranno sempre identica ampiezza e polarità istantanea.
Supponiamo altresì che ciascun idrofono, all'uscita del blocco amplificatore + filtro, generi una tensione efficace che definiamo rispettivamente
vs1' = 1 mV eff.
vs2' = 1 mV eff.

3)CARATTERISTICHE DELLA SOMMA
Applicando, tramite K1 e K2, le tensioni al sommatore, alla sua uscita, us, abbiamo i seguenti dati:

nel Caso A: dove le tensioni di rumore non sono identiche ne in ampiezza ne in polarità istantanee si ha:
solo k1 chiuso usn = 1 mv eff.
solo k2 chiuso usn = 1 mv eff.
k1 e k2 chiusi usn = 1.41 mV eff. per ( D > 10 λ )** ( λ = lunghezza d'onda = 1530 / f)
Questo è il caso della somma di due tensioni di rumore generiche che come tali si sommano secondo la radice quadrata della somma dei quadrati dei loro valori efficaci (somma tra potenze).
** La condizione D > 10 λ è imposta per avere una correlazione quasi nulla tra vn1' e vn2'.

nel Caso B: dove le tensioni di rumore sono identiche in ampiezza e polarità istantanee si ha:
solo k1 chiuso usn = 1 mv eff.
solo k2 chiuso usn = 1 mv eff.
k1 e k2 chiusi usn = 2 mV eff.
Questo è il caso della somma di due tensioni di rumore identiche che come tali si sommano linearmente secondo i loro valori efficaci.

nel Caso C: dove le tensioni di segnale sono identiche in ampiezza e polarità istantanee si ha:
solo k1 chiuso uss = 1 mv eff.
solo k2 chiuso uss = 1 mv eff.
k1 e k2 chiusi uss = 2 mV eff.
Questo è il caso della somma di due tensioni di segnale identiche che come tali si sommano linearmente secondo i loro valori efficaci.

4)ANALISI DEI VALORI DELLA SOMMA
Da quanto abbiamo visto in precedenza, per il rumore del mare, il valore della somma us nei casi A e B può presentarsi, in funzione di D, da un valore limite usn = 2 mv eff. per D = 0 ad un valore usn = 1.41 v eff. per D > 10 λ.
Nel caso C, del segnale, si ha uss = 2 mv eff. indipendente dal valore D.

In base alla definizione di "guadagno di direttività" ,G, inteso come rapporto tra il massimo segnale ed il rumore, nel caso in esame possiamo scrivere:
G = uss / usn
che nel caso in analisi può essere scritto :
G = uss / usn = 2 mV eff./ 2 mv eff. = 1 per D = 0
oppure
G = uss / usn = 2 mV eff./ 1.41 mv eff. = 1.41 per D > 10 λ

Si ha quindi una variabilità di G in funzione di D dovuta, come vedremo, dal coefficiente di correlazione esistente tra le due tensioni di rumore vn1' e vn2'.
Se D > 10 λ possiamo quindi scrivere:

G = uss / usn = (vs1' + vs2') / [ (ns1')² + (ns2')²]½

Se la base non fosse un dipolo ma un insieme lineare di m sensori omnidirezionali e la distanza tra due contigui fosse D > 10 λ il valore del guadagno di direttività potrebbe essere espresso con:
G = uss / usn = (vs1' + vs2' + .. + vsm') / [ (ns1')² + (ns2')²+ ... + (nsm')² ]½
Se consideriamo ora di valore unitario tanto i contributi vs che vn il valore di G diventa:
G = m /(m)½ ; razionalizzando si ha:
G = (m)½ ;
Il guadagno di direttività viene generalmente espresso in dB quindi:
G(dB) = 20 Log [(m)½ ]
G(dB) = 10 Log m
La formula si adatta sia al calcolo del G di una cortina che del dipolo:
per il dipolo m = 2 quindi: G(dB) = 10 Log 2 = 3 dB
per la cortina, se m = 10 ad esempio: G(dB) = 10 Log 10 = 10 dB
La formula alla quale siamo pervenuti, pur senza rigore formale, risponde ai risultati degli algoritmi, che esporremo nel paragrafo 7), ottenuti per via puramente analitica.
Chiudiamo questo paragrafo rimarcando infine che il "guadagno di direttività" di una base di sensori subacquei, nel presupposto D > 10 λ , è originato dal fatto che :
le tensioni idrofoniche dovute ai segnali si sommano linearmente mentre le tensioni idrofoniche dovute al rumore si sommano seconda la radice quadrata della somma dei loro quadrati.

5)SUL VALORE D > 10 λ
Si è visto che con il variare di D si passa da G = 1, per D = 0, a G = 1.41 per D > 10 λ; ciò a seguito del fatto che variando D varia il tempo di transito delle onde acustiche di rumore da un trasduttore all'altro.
Per D = 0 il tempo di transito è nullo e vn1' e vn2' sono uguali (massima coerenza); per D crescente cresce il tempo di transito Tt e si riduce la coerenza tra le due tensioni; Tt varia secondo l'espressione:
Tt = D / 1530.
Per avere un'indicazione della variabilità della coerenza di vn1' e vn2' in funzione di D si deve ricorrere alla funzione di correlazione di segnali a larga banda (si veda p5/cap.1.3.1.2/pag 47) opportunamente inserita nell'algoritmo empirico che esprime il guadagno di direttività (G) in funzione del numero dei sensori (m) e della funzione di correlazione (C) dipendente a sua volta dalla variabile D:

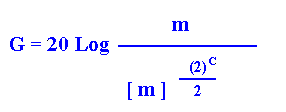
dove: C = [Sen(6.28 F Tt) / (6.28 F Tt)]
F = frequenza superiore della banda di vn1' e vn2'
Tt = D / 1530

L'algoritmo tradotto in linguaggio VB è :
y = (m ^ ((2 ^ c) / 2))
G = 20 * Log(m / y) / Log(10)

Un esempio dell'impiego dell'algoritmo per avere un'indicazione approssimata dell'andamento di G in funzione di D; supponiamo che siano:
F = 1500 Hz
m = 4
λ = 1530 /(1500) = 1 m
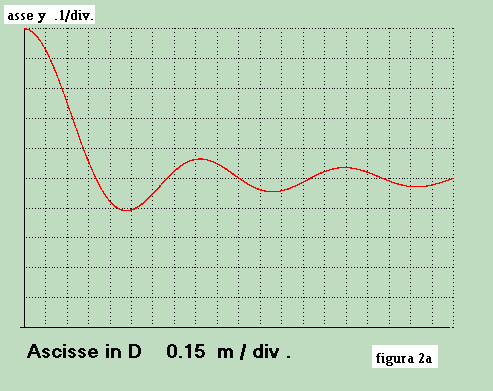
la curva, in funzione di D, che scaturisce dall'algoritmo è:



Dalla figura 2 si osserva che con il crescere del valore D il guadagno di direttività aumenta, ondulando, e tende al valore di 10 Log 4 = 6 dB per D >> λ.
Il guadagno massimo di direttività si ha per:
D = 4.7 div x 0.15 m / div = 0.7 m.

Per comprendere meglio il meccanismo della somma delle tensioni di rumore che ha generato la curva di figura 2 si può osservare la figura 2/a che mostra la varazione di tale somma in funzione di D.



Il valore massimo di usn si ha per D = 0, dove le tensioni che concorrono alla somma sono tutte identiche.
Il valore minimo di usn si ha per D = 4.7 dove le tensioni in parte si sommano ed in parte si sottraggono in base al loro grado di correlazione.
Infine quando D tende a valori molto superiori a λ la scorrelazione delle tensioni di rumore è massima è le stesse si sommano secondo le loro potenze.

6)GUADAGNO DI DIRETTIVITA' VERTICALE
I calcoli del guadagno di direttività illustrati nei paragrafi precedenti si riferivano a cortine di sensori omidirezionali estese in orizzontale; generalmente gli idrofoni che formano una cortina sono formati a loro volta da un insieme di sensori che sono posti lungo l'asse del trasduttore come si vede in figura 3.



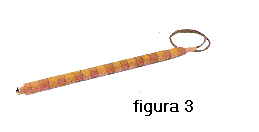
In virtù della loro geometria questi idrofoni sono omnidirezionali nel piano orizzontale e dotati di guadagno di direttività proprio nel piano verticale.
In questo caso il guadagno di direttività della base idrofonica è il prodotto dei due guadagni, l'uno relativo alla distribuzione in orizzontale dei sensori, l'altro relativo al guadagno di direttività verticale del singolo elemento di figura 3.
Il calcolo del guadagno di quest'ultimo è fattibile nello stesso modo sviluppato per le cortine idrofoniche orizzontali.
Il guadagno di direttività complessivo della nuova base tiene pertanto conto di:
Go = guadagno orizzontale di cortina
Gv = guadagno verticale del sensore
Se Go e Gv sono espressi in dimensioni lineari il guadagno totale GT = Go x GV
Se Go e Gv sono espressi in deciBel il guadagno totale GT(dB) = Go(dB) + GV(dB)

7)LE FORMULE CLASSICHE PER IL CALCOLO DEL GUADAGNO DI DIRETTIVITA'
Una volta appreso, di massima, qual'è la fisica che genera il guadagno di direttività delle basi idrofoniche possiamo prendere in esame gli algoritmi classici per il loro utilizzo nelle computazioni correnti.
Il primo algoritmo illustrao riguarda la base formata da due idrofoni, il dipolo:

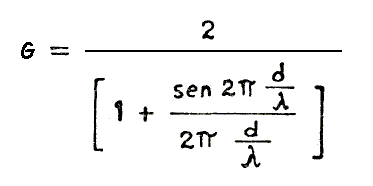
nella quale le due variabili sono:
d = distanza tra i due sensori
λ = 1530 / f
Il guadagno di direttività G non è espresso in deciBel.

La seconda formula è relativa al guadagno di direttività di una cortina d'idrofoni:

Per la cortina le variabili sono:
n = numero dei sensori
d = distanza tra i sensori
λ = 1530 / f
G non è in deciBel.

La terz'ultima formula riguarda una base idrofonica rettilinea e continua :

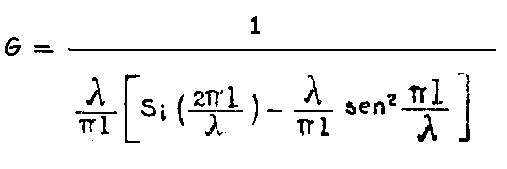
dove le variabili sono:
l = lunghezza della cortina
λ = 1530 / f
Si = integralseno

Come ultima una formula, empirica, per il calcolo del guadagno di direttività di ua base idrofonica di forma rettangolare:

Dove le variabili sono:
λ = 1530 / f
A = superficie della base
G non è in deciBel.

8)CALCOLO DEL GUADAGNO ( GT ) DAL PROFILO DELLE CARATTERISTICHE DI DIRETTIVITA'
Data una base rettangolare (la proiezione di una base cilindrica sulla sua generatrice potrebbe essere assunta come tale), se si conoscono i diagrammi di direttività (caratteristiche di direttività orizzontale e verticale si possono ricavare le larghezze dei lobi a - 3 dB per calcolare il guadagno di direttività GT con la formula :

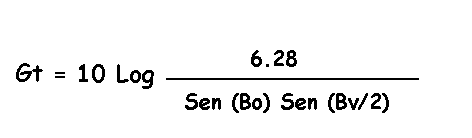
Dove:
con Bo s'intende la larghezza in gradi del lobo della caratteristica di direttività orizzontale misurato a -3 dB.
con Bv s'intende la larghezza in gradi del lobo della caratteristica di direttività verticale misurato a -3 dB.

Un semplice esempio:
siano date nelle figure 4 e 5 le caratteristiche di direttività di una base idrofonica rettangolare:





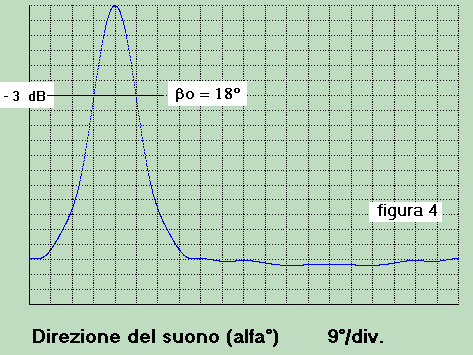
In figura 4 è rappresentata la curva di direttività orizzontale la cui larghezza a - 3 dB è Bo = 18°.
In figura 5 è rappresentata la curva di direttività verticale la cui larghezza a - 3 dB è Bv = 45°.
Applicando la formula otteniamo:
GT = 10 Log [ 6.28 / ( Sen 18° Sen 22.5°)] = 17 dB


Home

Stampa immagine grafica o descrizione testuale