SONAR-INFO-p61
Geometria analitica (4°)
La circonferenza con centro su (Xc ; Yc) e le sue tangenti
1)Generalità 2)Algoritmi in V.B. per la circonferenza con il centro su Xc ; Yc
r * sqr( m^2 + 1 ) = m * ( Xc - Xo ) + ( Yo - Yc )
-coordinate dei punti di tangenza X1t;Y1t e X2t;Y2t ottenute dalle espressioni:
X1t = (-m1 * n1) / (m1 ^ 2 + 1)
-computo dei coefficienti "a" , "b" , "c" relativi all'equazione della circonferenza:
a = -2 * Xc 3)Come si presenta la schermata del file eseguibile 4)Esempio d'utilizzo del programma di calcolo 5)Note
Per venire incontro a numerose richieste per l'estensione dei file eseguibili, dei tipi già
utilizzati in p55 e p57, per la soluzione di
altri problemi di geometria analitica, si illustrano alcune routine di calcolo per la soluzione
di casi diversi che possono essere utili a chi deve cimentarsi in questa
interessante parte della matematica.
Una premessa è necessaria prima del prosieguo della pagina: gli algoritmi utilizzati
non sono dimostrati ma soltanto implementati, a favore del calcolo automatico,
in apposite routine in Visual Basic; per le dimostrazioni si rimanda agli innumerevoli testi
di geometria analitica in commercio.
Quando le coordinate del centro della circonferenza sono su di un punto Pc = Xc ; Yc gli algoritmi
necessari per lo svolgimento dei problemi sono sensibilmente più complessi di quelli riportati
in p59 per la circonferenza con centro all'incrocio degli assi cartesiani.
In questa pagina è riportato un file eseguibile che consente, in modo rapido, il tracciamento di
una data circonferenza di raggio "r" e centro in P(Xc ; Yc) e, da un punto esterno ad essa,
la costruzione delle sue tangenti.
Il programma scrive inoltre l'equazioni delle rette in gioco, della circonferenza e le
coordinate dei punti di tangenza.
Gli algoritmi implementati, scritti in linguaggio V.B. sono:
-coordinate singoli punti : (Xa; Yb)
-equazione della circonferenza con centro su Pc( Xc ; Yc):
X^2 + Y^2 + aX + bY + c = 0
-equazione rette Y = m1 X + n1 e Y = m2 X + n2, tangenti alla circonferenza e passanti per il
punto P(Xo;Yo), ottenute dalla soluzione dell'equazione:
ed il conseguente calcolo di m1, n1 , m2, n2 con gli algoritmi:
a = Xc - Xo
b = Yo - Yc
m1 = (2 * a * b - Sqr(4 * a ^ 2 * b ^ 2 - 4 * (r ^ 2 - a ^ 2) * (r ^ 2 - b ^ 2))) / (2 * (r ^ 2 - a ^ 2))
n1 = Yo - Xo * m1
m2 = (2 * a * b + Sqr(4 * a ^ 2 * b ^ 2 - 4 * (r ^ 2 - a ^ 2) * (r ^ 2 - b ^ 2))) / (2 * (r ^ 2 - a ^ 2))
n2 = Yo - Xo * m2
X2t = (-m2 * n2) / (m2 ^ 2 + 1)
Y1t = n1 / (m1 ^ 2 + 1)
Y2t = n2 / (m2 ^ 2 + 1)
b = -2 * Yc
c = Xc^2 + Yc^2 - r^2
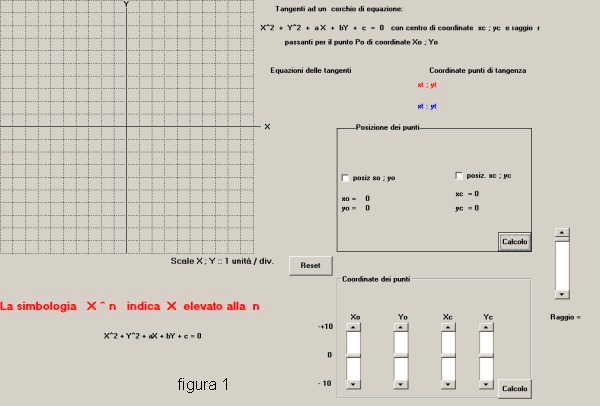
La schermata del file eseguibile, al lancio sul P.C, si presenta come mostrato in figura 1,
in essa s'individuano:
-il tracciato cartesiano
-l'area "Posizione punti" che comprende:
CheckBox a destra: per l'abilitazione al posizionamento di massima coordinate del centro, Xc;Yc, tramite il mouse
CheckBox a sinistra: per l'abilitazione al posizionamento di massima coordinate punto esterno, Xo;Yo, tramite il mouse
Pulsante avvio "Calcolo" dati d'area
-l'area "Coordinate dei punti" che comprende:
Due VscrollBar per il posizionamento preciso delle coordinate (Xo; Yo) del punto esterno
Due VscrollBar per il posizionamento preciso delle coordinate (Xc; Yc) del centro del cerchio
Pulsante avvio "Calcolo" dati d'area
-VscrollBar per l'impostazione del valore del raggio "r"
-Pulsante di "Reset" per l'azzeramento dei grafici e dei dati numerici
-scritta "equazioni delle tangenti" sotto la quale sono presentate l'equazioni computate
-scritta "coordinate punti di tangenza"
A seguito del calcolo compaiono le tre costanti a; b; c; relative all'equazione della circonferenza
In questo paragrafo sono proposti due esercizi grafico numerici la cui risoluzione è basata
sul file eseguibile (eserc.CnT) .
In entrambi i casi si risolve il problema classico del calcolo e tracciamento di una
circonferenza
, comunque collocata sul piano, e delle sue tangenti passanti per un punto esterno ad essa.
Il primo esercizio è relativo al posizionamento indicativo e veloce dei punti caratteristici
del problema: Con questa procedura è possibile orientarsi, non con precisione elevata,
sulle disposizioni più adatte alla impostazione del problema:
-posizione del punto esterno
-posizione del centro del cerchio
La procedura da seguire, svolta nell'area "Posizione punti", è la seguente:
1- spunta del CheckBox di sinistra (si abilita la funzione inserimento Po(Xo; Yo),punto esterno,
con il mouse)
2- muovendo il mouse si sceglie la posizione di Po, ad esempio nell'intorno di Xo = +3; Yo = -5,
e si clicca (compare sul reticolo il punto Po di colore blu) con Xo = +2.98; Yo = -4.98
3- si toglie la spunta del CheckBox di sinistra
4- spunta del CheckBox di destra (si abilita la funzione inserimento Pc(Xc; Yc),coordinate del
centro del cerchio, con il mouse)
5- muovendo il mouse si sceglie la posizione di Pc, ad esempio nell'intorno di Xc = -2; Yc = +4
e si clicca (compare sul reticolo il punto Pc di colore rosso) con Xc = -1.98; Yc = 3.95
6- con -VscrollBar del raggio si sceglie r = 3
7- pigiando il pulsante "Calcolo" dell'area prescelta si ha la presentazione della schermata
riportata in figura 2:
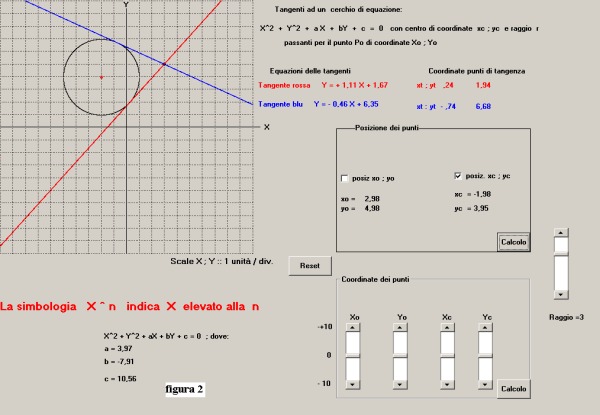
Il risultato complessivo dell'esercizio porta ai seguenti dati:
1) coordinate del punto esterno: Xo = +2.98; Yo = -4.98
2) coordinate del centro della circonferenza: Xc = -1.98; Yc = 3.95
3) valore del raggio: r = 3
4) equazione delle rette tangenti

5) coordinate dei punti di tangenza

6)Coefficienti a; b; c; dell'equazione della circonferenza X^2 + Y^2 + aX + bY + c = 0
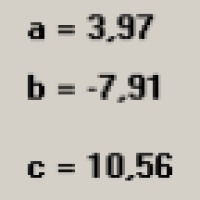
L'esempio può essere ripetuto, per diverse impostazioni indicative di altri problemi,
dopo la pressione del pulsante "Reset" che cancella tutta la grafica ed azzera tutta l'impostazione numerica.
Una volta individuata la geometria desiderata è possibile procedere ad un'impostazione precisa del
problema utilizzando l'area "Coordinate dei punti" così come di seguito indicato.
Il secondo esercizio è relativo al posizionamento preciso dei punti caratteristici
del problema:
In questo modo è possibile risolvere il problema posto con precisione
elevata
La procedura da seguire, svolta nell'area "Coordinate dei punti", è la seguente:
1)- con i due VscrollBar di sinistra s'impostano le coordinate di Po; ad esempio
Xo = -7.4 ; Yo = +3.2
2)- con i due VscrollBar di destra s'impostano le coordinate di Pc; ad esempio
Xc = 4.1 ; Yc = -2.6
3) con il VscrollBar del raggio si pone r = 4.5
4) pigiando il pulsante d'area "Calcolo" si ha la presentazione precisa riportata in figura 3:
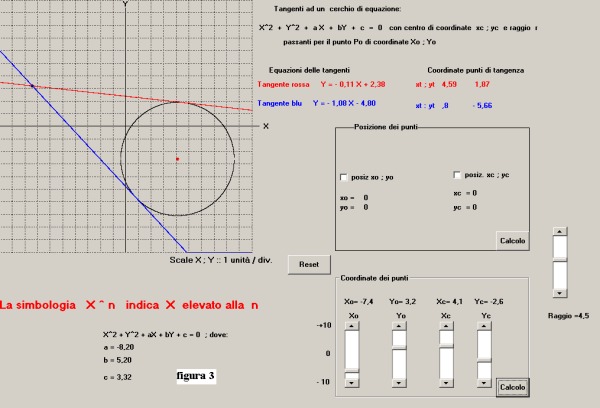
Il risultato complessivo dell'esercizio porta ai seguenti dati:
1) coordinate del punto esterno: Xo = -7.4; Yo = +3.2
2) coordinate del centro della circonferenza: Xc = 4.1; Yc = -2.6
3) valore del raggio: r = 4.5
4) equazione delle rette tangenti
5) coordinate dei punti di tangenza

6)Coefficienti a; b; c; dell'equazione della circonferenza X^2 + Y^2 + aX + bY + c = 0

L'esempio può essere ripetuto dopo la pressione del pulsante "Reset" che cancella tutta la grafica
ed azzera tutta l'impostazione numerica.
-Generalmente i problemi scolastici di geometria analitica mostrano, in tutti i casi, l'impiego
di numeri razionali (frazioni numeriche) o irrazionali (radici quadrate) per l'eleganza formale
del testo; è naturale quindi che per il controllo dei risultati di un problema di tipo scolastico
con l'analogo sviluppato con le nostre routine si dovranno trasformare i valori razionali o
irrazionali esposti per il primo in valori decimali per il confronto con il secondo.
-Il controllo software del file eseguibile è stato eseguito al meglio; è possibile però che
qualche particolare anomalia sia sfuggita all'esame.
Si prega pertanto chi dovesse riscontrare qualche difetto nell'impiego del programma di renderlo
noto tramite " Contatti con l'autore"; si provvederà all'aggiustaggio in rete.