Geometria analitica (17°)
Intersezioni tra l' ellisse e la circonferenza con centri nell'origine degli assi.

1)Generalità
Per venire incontro a numerose richieste per l'estensione dei file eseguibili, dei tipi già utilizzati in p55 e p57, per la soluzione di altri problemi di geometria analitica, si illustrano alcune routine di calcolo per la soluzione di casi diversi che possono essere utili a chi deve cimentarsi in questa interessante parte della matematica.
Una premessa è necessaria prima del prosieguo della pagina: gli algoritmi utilizzati non sono dimostrati ma soltanto implementati, a favore del calcolo automatico, in apposite routine in Visual Basic; per le dimostrazioni si rimanda agli innumerevoli testi di geometria analitica in commercio.

2)Algoritmi in V.B. per le intersezioni dell'ellisse con la circonferenza.
Quando le coordinate del centro dell'ellisse e della circonferenza sono coincidenti con l'intersezione degli assi cartesiani di riferimento si ha il caso più semplice per la soluzione dei problemi tra queste due coniche.
In questa pagina è riportato un file eseguibile che consente, in modo rapido, il tracciamento tra un'ellisse di fuochi F1 = c; F2 = -c e centro in Pe(Xe = 0 ; Ye = 0) e di una circonferenza di centro Pc(Xc = 0 ; Yc = 0) e raggio R; quindi il calcolo delle coordinate dei punti di contatto.
Gli algoritmi implementati, scritti in linguaggio V.B. sono:

-equazione dell'ellisse con centro all'origine degli assi:
((X^2) / (a^2) ) + ((Y^2) / (b^2) ) = 1
-coordinate dei fuochi : F1 (X1 = c; Y1 = 0) ; F2 (X2 = -c; Y2 = 0)
-coordinate dei punti di intersezione asse X : P1 (X3 = a; Y3 = 0) ; P2 (X4 = -a; Y4 = 0)
-coefficiente b: b = sqr( a^2 - c^2)
-l'equazione della circonferenza:
X^2 + Y^2 = R^2
Ciò per la soluzione del sistema:
((X^2) / (a^2) ) + ((Y^2) / (b^2) ) = 1
X^2 + Y^2 = R^2
che consente il calcolo delle coordinate di quattro punti d'intersezione; simmetrici rispetto agli assi del reticolo cartesiano.

3)L'impiego del file eseguibile
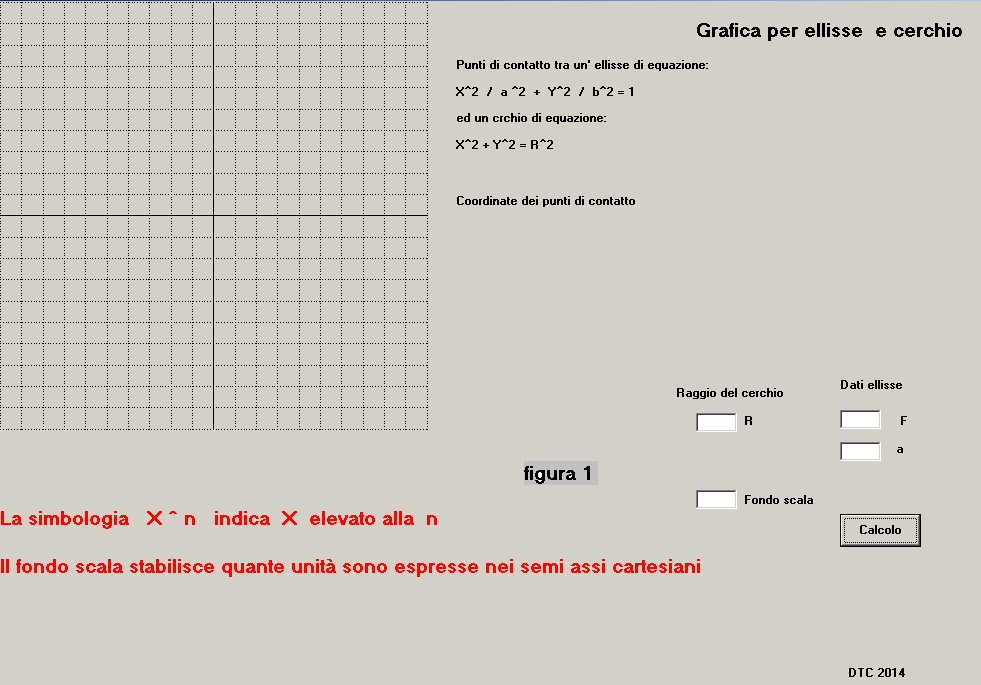
Il file eseguibile, al lancio sul P.C, si presenta come mostrato in figura 1, in essa s'individuano il tracciato cartesiano e 4 caselle d'immissione dati con un pulsante d'avvio "Calcolo".
Nella casella "R" si deve digitare il valore del raggio della circonferenza.
Nella caselle "F" l'ascissa dei fuochi
Nella casella "a" l'ascissa del punto di contatto dell'ellisse con l'asse x
Nella casella "Scala" il valore da assegnare al fondo scala del reticolo affinché possa contenere il tracciato completo: ellisse più tangenti.
Sotto la scritta " Coordinate dei punti d'intersezione" vengono presentati i dati del calcolo.

4)Esempio d'utilizzo del programma di calcolo
In questo paragrafo viene proposto un esercizio grafico numerico la cui risoluzione è basata sul file eseguibile (eserc.ellc) .
Il calcolo che ci accingiamo a svolgere richiede una semplice osservazione:
Il problema non ammette soluzioni se la circonferenza ha R > a (la circonferenza contiene l'ellisse)
Il problema non ammette soluzioni se la circonferenza ha R < b (la circonferenza è contenuta dall'ellisse)
La soluzione del problema viene sviluppata in una frazione di minuto.
Ipotizziamo la ricerca dei punti d'intersezione tra un' ellisse di centro nell'origine degli assi, con: F1 = +7; F2 = -7; a = 8, ed una circonferenza di raggio R = 5 anch'essa con centro all'origine degli assi
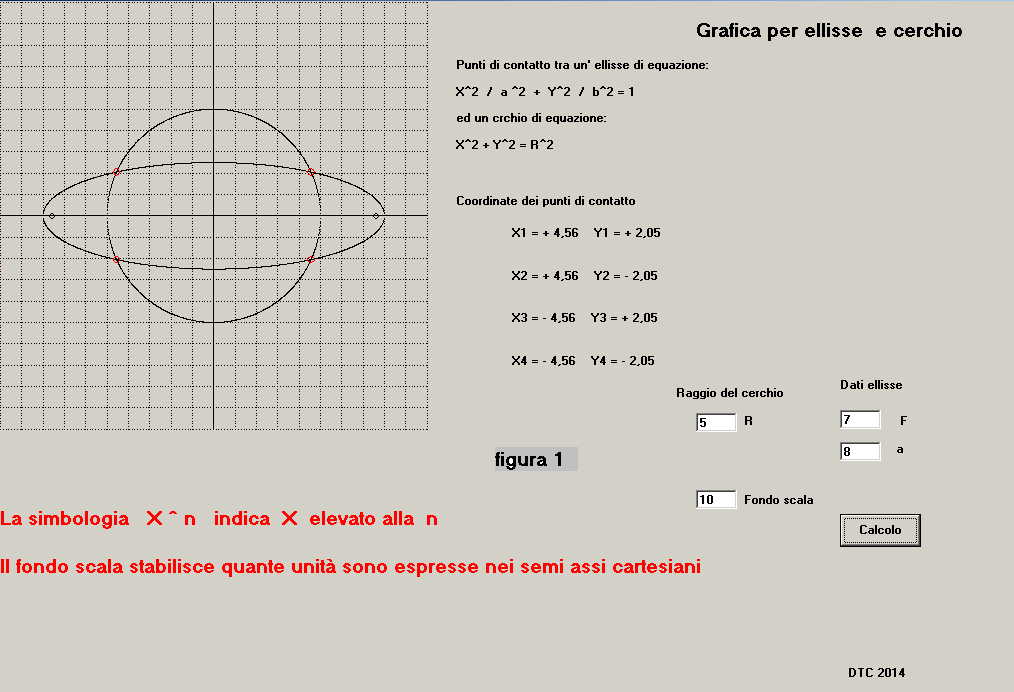
Una volta inseriti i dati nelle apposite caselle della schermata di (eserc.ellc), con valore di fondo scala uguale a 10, otteniamo i seguenti dati come mostrato in figura 2:

5)Note
-Generalmente i problemi scolastici di geometria analitica mostrano, in tutti i casi, l'impiego di numeri razionali (frazioni numeriche) o irrazionali (radici quadrate) per l'eleganza formale del testo; è naturale quindi che per il controllo dei risultati di un problema di tipo scolastico con l'analogo sviluppato con le nostre routine si dovranno trasformare i valori razionali o irrazionali esposti per il primo in valori decimali per il confronto con il secondo.

-Il controllo software del file eseguibile è stato eseguito al meglio; è possibile però che qualche particolare anomalia sia sfuggita all'esame.
Si prega pertanto chi dovesse riscontrare qualche difetto nell'impiego del programma di renderlo noto tramite " Contatti con l'autore"; si provvederà all'aggiustaggio in rete.