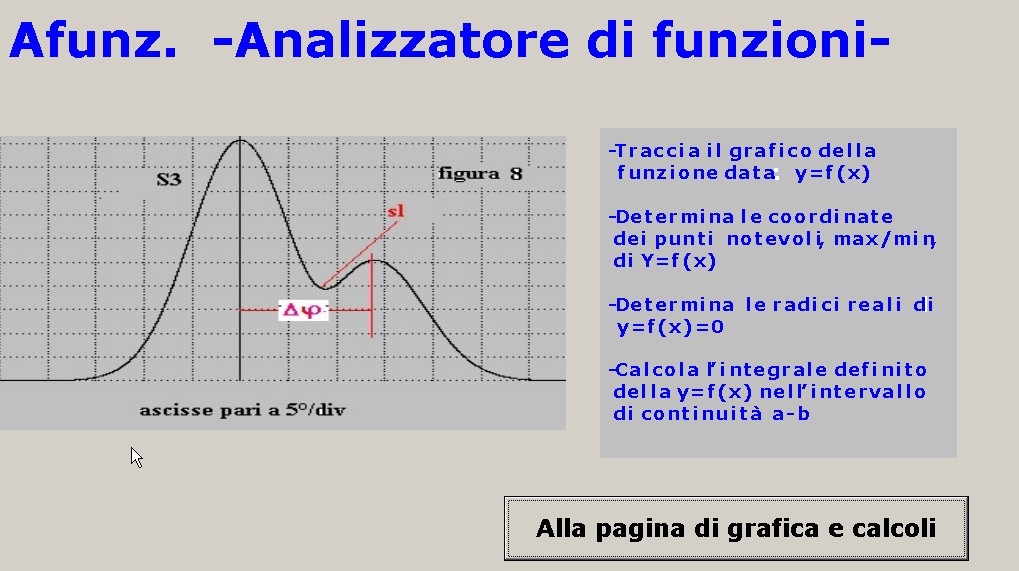figura 1

Il pannello operativo, riportato in figura 2, è di seguito commentato:

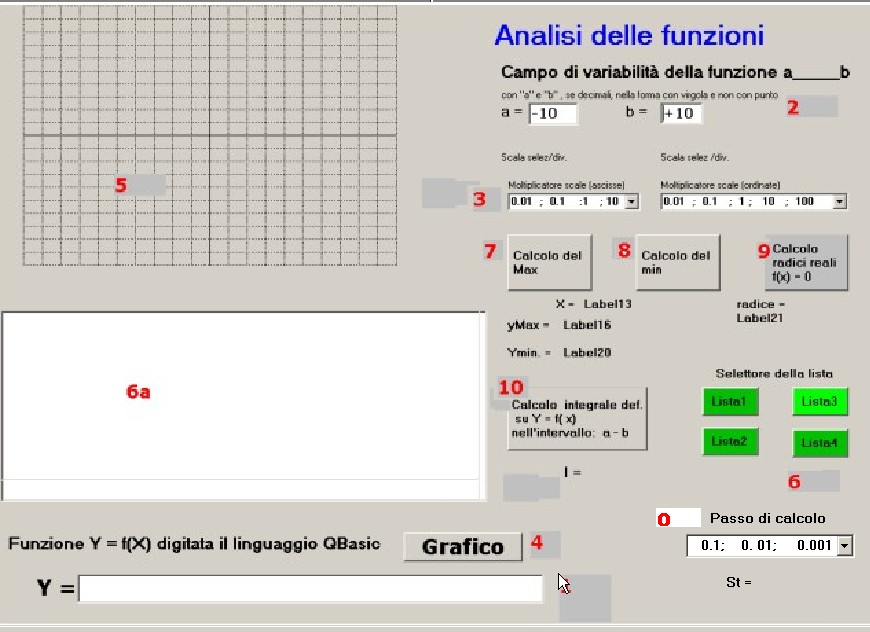figura 2

Con riferimento ai numeri in rosso la sequenza operativa delle azioni da compiere per l'analisi di una funzione:

0) impostazione del passo di calcolo; al lancio del programma è: st = 0.001; puo essere selezionato:
st = 0.1; st = 0.01; st = 0.001; st = 0.0001.
Più il passo di calcolo è piccolo maggiore è la precisione e superiore è il tempo di elaborazione.

1) digitazione nel textbox,in linguaggio QBasic, della funzione matematica da analizzare

2) impostazione dei limiti del campo di continuità di Y = f(x), possono assumere qualsiasi valore entro -10 e +10, al lancio del programma abbiamo: a = -10; b = +10. Si deve ricordare che i valori digitati, se decimali, devono essere scritti con la virgola: ad esempio 4,34.
Per le operazioni di calcolo di Max; min ; radici; integrali è opportuno che i limiti a - b siano posizionati all'intorno dei punti interessati.

4) pressione del pulsante "Grafico" per l'avvio delle operazioni

5) visione del grafico di y = f(x) che compare nel tracciato cartesiano

3) modificazione o aggiustaggio della scala del tracciato se necessario ; le scale al lancio del programma sono ascisse 1/div. ; ordinate 1/div.

6) captazione della serie di coordinate di f(x) nel campo di variabilità impostato in 2; l'operazione può essere fatta per 4 liste diverse, ciascuna utilizzabile per una sola volta, una volta premuto il pulsante, ad esempio "lista1" il pulsante cambia colore in rosso per indicare che una lista dei valori è stata acquisita; la lista1 non è più utilizzabile salvo ad un nuovo lancio del programma, altre 3 liste possono essere compilate tramite gli appositi pulsanti. La compilazione delle liste per un analisi di f(x) è consigliabile, una volta stabilito l'intervallo d'analisi ( a -b ) con il passo di calcolo "st", minimo ( 0.1 ), onde evitare, almeno all'inizio, liste troppo lunghe e difficilmente consultabili; restringendo l'intervallo ( a - b ) si può ridurre il passo di calcolo.
Una volta che tutti i pulsanti sono rossi si deve riavviare il programma.

6a)lettura nel listbox della serie di valori acquisiti in lista1, con la slitta verticale si possono visionare tutte le coppie x;y che definiscono il grafico di y = f(x) in 5). Se necessario riportare dati sulla carata si può operare con il copia-incolla.

7)dopo apposizione limiti intervallo a - b e st = 0.001, in base alle necessità, calcolo delle coordinate dei massimi di y = f(x)

8)dopo apposizione limiti intervallo a - b e st = 0.001, in base alle necessità, calcolo delle coordinate dei minimi di y = f(x)

9)dopo apposizione limiti a - b e st = 0.0001, in base alle necessità, calcolo delle radici reali di f(x) = 0

10)calcolo, se necessario, dell'integrale definito di y = f(x) nell'intervallo a - b e st = 0.001, ; il valore compare nel label indicato con I =.

Afunz è corredato da un comando, pulsante in basso a destra, con il quale è possibile uscire dall'eseguibile in qualsiasi momento si renda necessario.

3) Esempio d'impiego dell'analizzatore di funzioni ( 1°)

Lanciamo Afunz.exe: Eseguibile
Iniziamo in modo semplice sul pannello operativo fissando il passo di calcolo: mediano st = 0.01, utilizzando la funzione parabolica riportata in 2.1), per k = 4 che riportiamo con la conversione in QBasicc;
Y = x² + x + 4 la sua corrispondente in QBasic è:
y = x^2 + x + 4
Digitiamo la funzione in locazione 1 così come riportato in figura 3:

figura 3

Confermiamo, in figura 4, i limiti del campo d'analisi per a = -10 e b = +10 secondo la locazione 2:

figura 4

Confermiamo, in figura 5, i valori di scala: ascisse 1/div.; ordinate 1/div. secondo la locazione 3:

figura 5

Si preme ora il pulsante "grafico" in locazione 4 per ottenere il grafico della funzione data nel reticolo cartesiano, locazione 5; l'andamento della funzione è mostrato in figura 6:

figura 6

In figura 6 si vedono, oltre la curva data di y = f(x), anche due linee verticali di colore viola che indicano il campo di analisi, nel nostro caso a -10 a sinistra e + 10 a destra.

Possiamo ora generare la lista1, su pressione del primo pulsante della locazione 6, per ottenere la lista, in locazione 6a, che contiene 1000 coppie di coordinate x;y che definiscono in dettaglio la curva; una parte dei dati visibili è riportata in figura 7:

figura 7

Facendo scorrere la slitta verticale, destra, si possono leggere tutti i dati presenti in lista1.
Se siamo interessati alla determinazione delle coordinate del minimo, punto notevole della curva, dal tracciato si può valutare, in prima approssimazione, che il minimo è collocato tra x = - 1 e x = 0.
Con i limiti sopra individuati: a = -1 ; b = 0 e con il minore valore per "st", st = 0.001, s'impostano su locazione 0 e 2 tali valori. Premuti in sequenza il pulsante "grafica" e "calcolo min." in locazione 7 si hanno i valori delle coordinate del minimo come illustrato in figura 8:

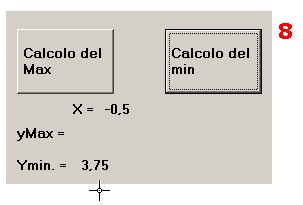figura 8

Analogo risultato si ottiene con la derivata prima di y = , uguagliata a 0 :
y = x² + x + 4
y' = 2 x + 1
2 x + 1 = 0; x = - 0.5 ( ascissa del minimo )
ym = -0.5² - 0.5 + 4 = 3.75 ( ordinata del minimo)

Con l'analizzatore, tramite la locazione 10, è possibile calcolare l'integrale definito di
y = x² + x + 4 ; ad esempio nello stesso intervallo posto per la ricerca del minimo di y = f(x).
Per tale ricerca abbiamo assunto a = -1 e b = 0 e st = 0.001; una volta premuto il pulsante "grafica" la locazione 5 assume l'aspetto di figura 9:

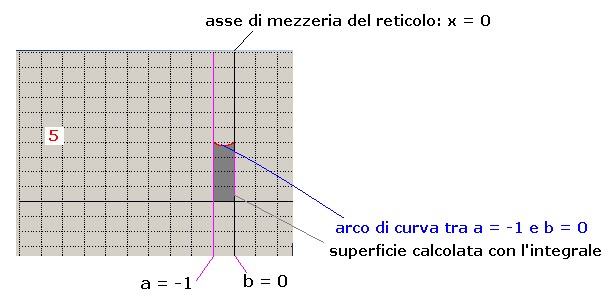figura 10


Premendo di seguito il pulsante 10 si ha il valore dell'integrale così come mostra figura 8:

figura 10

A conferma del risultato possiamo calcolare l'integrale definito di:
y = x² + x + 4 secondo le regole dell'analisi matematica:
I = ∫ ( x² + x + 4)dx = [ x³/3 + x²/2 + 4 x ] tra a = -1 e b = 0
I = - ( - 1/3 + 1/2 - 4 ) = 1/3 - 1/2 + 4 = 3.833333
come possiamo vedere il calcolo con Afunz porta ad un errore, rispetto al processo analitico dell'ordine di 1/10000.

4) Esempio d'impiego dell'analizzatore di funzioni ( 2° )

Sia data la funzione:
y = 2 x³ + x² - 5 x + 1
che trasformata in QBasic assume la forma:
y = 2 * x^3 + x^2 - 5*x + 1
Lo studio di questa funzione si presta ad un utilizzo totale di Afunz come si evince dai seguenti passaggi, dove, per comodità editoriali, il reticolo cartesiano 5 viene mostrato soltanto nella parte che contiene la curva :

p1) Si traccia la curva e si compila lista 1 per st =0.01; si vedano figure 11 e 12:

figura 11

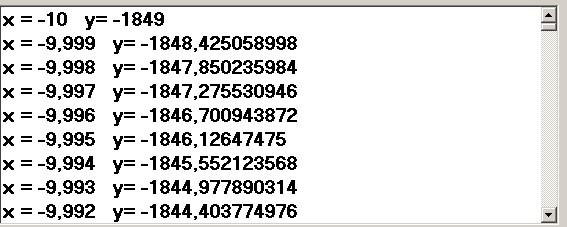figura 12

p2) Si calcolano le coordinate del massimo tra a = -2 e b = 0 per st =0.001; si vedano figure 13 e 14

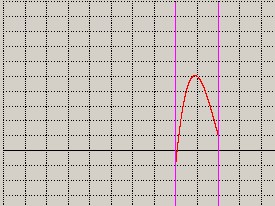figura 13

figura 14

p3) Si calcolano le coordinate del minimo tra a = 0 e b = 2 per st =0.001; si vedano figure 15 e 16

figura 15

figura 16

p4) Si calcola la prima radice di f(x) = 0 per a = -2.5 e b = -1 per st =0.0001 ; si vedano figure 17 e 18

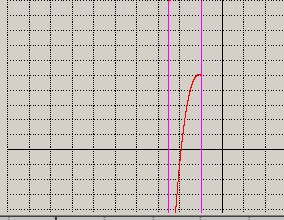figura 17

figura 18

p5) Si calcola la seconda radice di f(x) = 0 per a = 0 e b = 1 per st =0.0001 ; si vedano figure 19 e 20

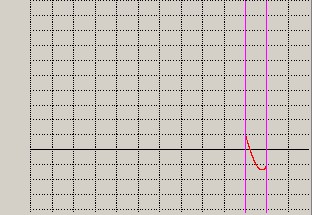figura 19

figura 20

p6) Si calcola la terza radice di f(x) = 0 per a = 1 e b = 2 per st =0.0001; si vedano figure 21 e 22

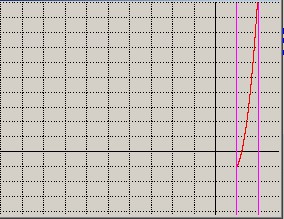figura 21

figura 22

p7) Si calcola l'integrale di f(x) per a = -2 e b = 0 per st =0.0001; si vedano figure 23 e 24

figura 23

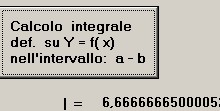figura 24

A1) Appendice 1 - Osservazionei sui file eseguibili-

Questo sito contiene innumerevoli file exe come ausilio ai calcoli specifici sulle tre materie trattate: Tecniche sonar; Tecniche di correlazione; Processi matematici e di geometria analitica.
Come ben sappiamo i programmi antivirus installati sui P.C. ( in special modo i modelli recenti ) rifiutano a priori, senza chiedere il permesso all'utilizzatore, l'apertura dei file con estensione exe che per natura potrebbero essere pericolosi per il P.C.
Il comportamento degli antivirus è naturale ma impedisce al fruitore di questo sito la possibilità di utilizzare una notevole mole di file di calcolo che sono frutto di un'esperienza di oltre 50 anni di lavoro specifico.
Quando la rete e i primi P.C. sono stati messi a disposizione dei tecnici, desiderosi di acquisire nuove conoscenze, questi si sono lanciati alla ricerca di articoli e di file eseguibile che potessero aiutarli nel proprio lavoro quotidiano.
Questa procedura ha portato si a qualche cattivo incontro ma altresì ha contribuito alla diffusione delle conoscenze nell'ambito di tutte le tecniche che richiedevano complessi metodi di calcolo affrontabili, grazie al lavoro di altri, con i fie.exe.
I file eseguibili disponibili nelle pagine di questo sito sono tutti compilati con lo stesso strumento informatico :

VISUAL BASIC 5 / 6 della Windows

Ora rendendoci ben conto che chi possiede un moderno ed efficiente P.C. ci pensa due volte a rischiarne la corretta funzionalità aprendo un file exe non conosciuto, possiamo tentare di dirottare i file exe necessari al nostro lavoro su P.C. non recenti, quelli per intenderci che ci chiedono se vogliamo aprire un file exe o no, lasciando a noi la decisione ed il rischio conseguente.
Io non posso altro che riportare 3 email, una inviata a me, le altre due tra tecnici norvegesi ben felici di aver trovato tra le pagine di questo sito l'eseguibile : p5/esercor.exe (compilato con lo stesso VB 5/6 indicato in precedenza) utile per il calcolo ed i grafici delle funzioni di correlazione; ecco le Email; ciascuno si comporti quindi come meglio crede assumendosi le proprie responsabilità:

A2)Appendice 2 - Pagine di conversione in linguaggio QBasic -
Sono riportate di seguito, secondo quanto esposto nel testo illustrato su su p11 , alcune pagine di conversione simbolica:

Home

Stampa immagine grafica o descrizione testuale