SONAR-INFO-p100
ANALISI DETERMINISTICA E STATISTICA 1)Generalità 2)Definizioni della terminologia in modo estremamente semplice 3)Esame dell'impulso d'eco 4)Esempio di calcolo dello spettro di un impulso 5)Esame di un segnale di rumore 6)Esempio di calcolo del rumore rivelato
Esempi d'impiego per i segnali sonar
La teoria relativa ai segnali elettrici ed alla loro analisi è molto complicata,
il suo apprendimento richiede lo studio di numerosi testi specialistici.
Su questa pagina, pertanto, ci limitiamo ad esporre, in modo strettamente tecnico, alcune
funzioni che consentono l'esame di due segnali caratteristici del sonar senza entrare
nelle dimostrazioni matematiche.
L'analisi deterministica dei segnali elettrici è rivolta ai segnali definibili
matematicamente mediante una o più variabili invarianti nel tempo.
La definizione di dette variabili può essere espressa, indifferentemente, sia in funzione
del tempo, sia della frequenza; il passaggio tra le due rappresentazioni avviene attraverso
alcune trasformazioni analitiche legate all'analisi armonica di Fourier;
la diversa rappresentazione delle variabili dipende dalle necessità d'uso.
Un esempio semplice di segnale deterministico è relativo all'impulso d'eco riflesso da un
bersaglio in assenza di riverberazione e di rumore.
L'analisi statistica dei segnali elettrici è rivolta ai segnali le cui caratteristiche
nel tempo non sono definibili tramite precise funzioni matematiche dato che il loro comportamento è
aleatorio, il valore nel tempo di in segnale aleatorio nen è ripetibile, di questo è possibile
stabilirne soltanto il valore più probabile secondo espressioni derivate dalla teoria delle
funzioni casuali.
Esempio di un segnale aleatorio è, con molta approssimazione, il rumore emesso
da un semovente navale.
Come accennato nel paragrafo 2) un segnale deterministico è individuabile nell'impulso d'eco riflesso
da un bersaglio a seguito dell'emissione del sonar.
L'analisi deterministica di questo tipo d'impulso è fondamentale per stabilire la larghezza di banda
del ricevitore sonar delegato alla sua ricezione; procediamo all'esame:
sia dato l'impulso d'eco, di durata T = t2-t1, riportato in figura 1.
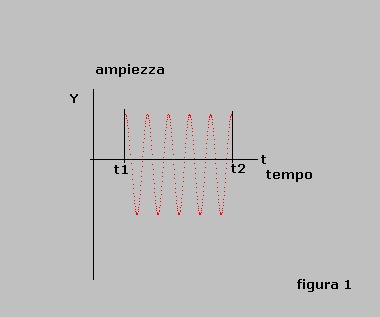
Questo segnale, funzione del tempo, è definibile matematicamente secondo l'espressione:
Y = 0 per t1 > t > t2
Y = A Cos ωo t per t1 ≤ t ≤ t2
dove ωo = 2 Π fo con fo = frequenza dell'onda dell'impulso.
Per stabilire la larghezza di banda del filtro che deve ricevere l'impulso si deve trasformare
la funzione Y = f(t), espressa nel dominio del tempo, nella funzione G = f( ω) -spettro
dell'impulso- espressa nel dominio della frequenza, tramite un processo d'analisi
deterministica individuabile nell'integrale di Fourier sotto riportato:
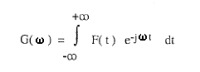
dove ω = 2 Π f con f = frequenza dello spettro.
Il risultato dello sviluppo dell'integrale di Fourier conduce alla funzione G( ω ) di seguito
indicata:
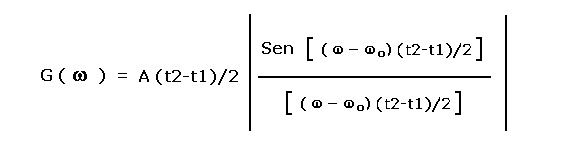
La G( ω ) è caratterizzata dal valore assoluto della nota funzione Sen x / x con ω variabile
da - ∞ a + ∞ ; lo spettro si estende indefinitivamente per frequenze superiori ed inferiori
a ωo secondo l'andamento riportato in figura 2:
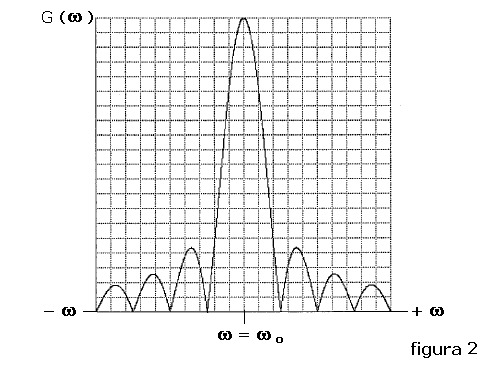
La curva può essere tracciata, con lo stesso profilo, in funzione di f in vece di ω così
come sarà fatto, per chiarezza, nell'esempio di paragrafo 4).
Sia dato l'impulso di figura 1 con le seguenti caratteristiche:
- durata T = (t2-t1) = 0.002 Sec.
- frequenza fo = 10000 Hz
- ωo = 2 Π fo = 6.28 x 10000 Hz = 62800
- ampiezza A = 1000
Applicando la funzione per il calcolo di G( ω ) otteniamo la curva dello spettro di
frequenza riportata in figura 3:
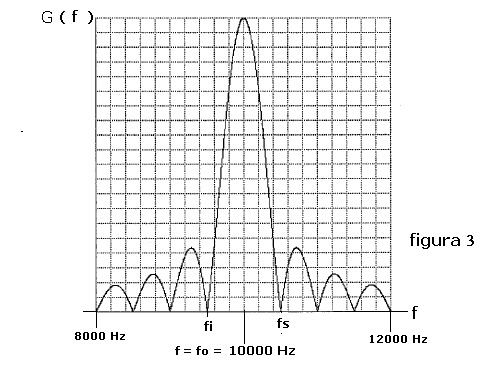
dalla curva si osserva:
- la curva è tracciata in un campo di frequenza compreso tra 8000 Hz e 12000 Hz
- il massimo della funzione si ha per f = fo = 10000 Hz, ovvero per ω = ωo = 62800
- esiste una frequenza fi, inferiore a fo, per la quale l'ampiezza dello spettro si annulla
il valore di fi è calcolabile con l'espressione :
fi = fo - [ 1 /( t2-t1 )] = 10000 - ( 1 / 0.002 ) = 9500 Hz
- esiste una frequenza fs, superiore a fo, per la quale l'ampiezza dello spettro si annulla
il valore di fs è calcolabile con l'espressione :
fs = fo + [ 1 /( t2-t1 )] = 10000 + ( 1 / 0.002 ) = 10500 Hz
Per la valutazione della larghezza di banda del ricevitore delegato alla ricezione dell'impulso
il cui spettro è individuato in figura 3 sono necessarie due considerazioni:
- lo spettro si estende indefinitivamente per frequenze rispettivamente inferiori e superiori di fo
- il prevalente contenuto di energia è contenuto nell'intervallo fs-fi, oltre il quale i valori
d'ampiezza dello spettro si riducono progressivamente a livelli trascurabili
E' d'uso pertanto assumere la larghezza di banda BW del filtro del ricevitore pari a:
BW = fs-fi; nel nostro esempio BW = fs - fi = 1000 Hz
tenendo poi in considerazione anche l'ulteriore estensione della banda a seguito dell'effetto Doppler previsto.
Chiudiamo il paragrafo con una semplice formula che consente il calcolo immediato della larghezza di banda del
filtro:
indicata con T = t2-t1 la durata dell'impulso si ha: BW = 2 / T
Come accennato nel paragrafo 2) un segnale statistico è individuabile, con una certa
approssimazione, nel rumore ricevuto dal sonar a causa dell'irraggiamento generato dai semoventi.
L'analisi statistica di questo tipo di segnale, la cui presentazione nel dominio del tempo è
riportata in figura 4, è fondamentale per stabilire le caratteristiche del segnale in uscita dal
rivelatore del sonar.
Il segnale di figura 4 non può essere definito mediante un'espressione determinata ma tramite un
insieme di condizioni e variabili sotto elencate:
- il rumore deve essere definito all'interno di una banda stabilita
- all'interno della banda la densità dello spettro deve essere uniforme (rumore gaussiano)
- BWn = banda delle frequenze che formano il rumore
- δ = deviazione standard = valore efficace del rumore all'interno della banda
- δ² = varianza del rumore all'interno della banda
Se le condizioni poste sono valide la presentazione del rumore nel dominio della frequenza
ha lo stesso profilo del filtro di banda che lo caratterizza, si veda figura 5:
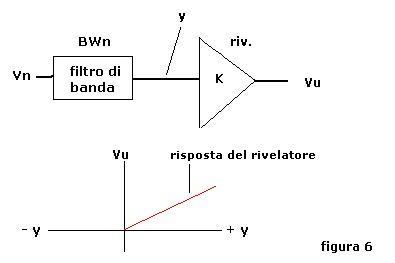
Per la determinazione dell'andamento del segnale di rumore all'uscita del rivelatore del sonar
è necessaria la definizione matematica del rivelatore stesso, figura 6, che si concretizza con:
vu = 0 per y < 0
vu = k y per y > 0
Lo spettro della tensione vu all'uscita del rivelatore, che definisce il segnale utile per il sonar,
è calcolabile con un processo di analisi statistica complesso ed elaborato che conduce ad uno
spettrogramma del tipo indicato in figura 7:
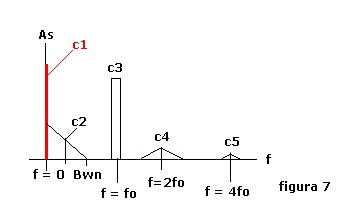
I simboli nella trattazione che segue sono:
BWn = larghezza di banda del filtro (figura 6)
fo = frequenza centrale del filtro
c1 .. c5 ... componenti dello spettro (dominio della frequenza)
f = ascissa delle frequenze
As = ordinata delle ampiezze dello spettro
K = guadagno del rivelatore
δ = livello di rumore all'interno della banda
Le diverse componenti dello spettro sono nell'ordine:
- c1 per f = 0 : c1 = K δ / √( 2 Π ) componente cc in uscita dal rivelatore ( segnale per il sonar)
- c2 livello medio tra f = 0 e BWn : componente spettrale residua (varianza di rivelazione):
vr = [0.5 K δ / √( 8 Π BWn)] / √(Hz)
- c3 piccola banda di segnale attorno alla frequenza centrale di BWn
- c4 piccola banda di segnale attorno a 2fo
- c5 piccola banda di segnale attorno a 4 fo
- cn...
Nella componente c1 si può ridurre l'effetto di c2 ed eliminare le altre, non utili al trattamento
sonar, tramite un adatto filtro integratore (RC) collegato in uscita al rivelatore.
La rivelazione del rumore dei semoventi, a scopo di ricerca sonar, è impostata in base allo
schema di figura 8, derivato da figura 6:
Dati per il calcolo:
-densità spettrale all'ingresso del filtro: vn = 7.6 mVeff / √(Hz) = +17.6 dB / mVeff / √(Hz)
-frequenza centrale del filtro passa banda: fo = 11000 Hz
-larghezza del filtro passa banda: BWn = 7000 Hz
-perdita del filtro passa banda 0 dB
-guadagno del rivelatore K = 32 dB
-costante di tempo dell'integratore: RC = 1 Sec.
-banda dell'integratore: bwrc = 1 / (2 Π RC) = 0.16 Hz
-attenuazione integratore in cc: att.cc = 0 dB
Sviluppo dell'esempio:
1) determinazione del livello all'uscita del filtro di banda BWn :
y = δ = 17.6 dB / mVeff / √(Hz) + 10 log 7000 = + 56 dB/mVeff = 631 mVeff
2) computo della componente Vcc = c1 all'uscita del rivelatore + integratore :
c1 = K δ / √( 2 Π ) = 32 dB + 56 dB/mVeff - 8 db = 80 dB/mVcc = 10 Vcc
3) livello spettrale di vr :
vr = [0.5 K δ / √( 8 Π BWn)] / √(Hz)
vr = -6 db + 32 dB + 56 dB - 52 dB = + 30 dB / √(Hz)
4) calcolo della varianza Var.Int all'uscita dell'integratore RC :
Var.Int = vr + 10 log (bwrc) = + 30 dB - 8 dB = + 22 dB / mVeff = 12 mVeff