SONAR-INFO-p102
Sistemi sonar attivi I parametri acustici 1) PREMESSA 2) GENERALITA' 3) IL PARAMETRO ACCURATEZZA E IL RAPPORTO S/D 4) IL PARAMETRO RISOLUZIONE IN PRESENZA DI PIU' VARIABILI ACUSTICHE 5)IL PARAMETRO PRECISIONE 6) ILLUSTRAZIONE DEL PARAMETRO ACCURATEZZA 7) ILLUSTRAZIONE DEL PARAMETRO RISOLUZIONE 8) ILLUSTRAZIONE DEL PARAMETRO PRECISIONE
Lo studio dei parametri acustici del sonar attivo, indicati come:
accuratezza, risoluzione, precisione,
è tra i più complessi tra la diversa tipologia di argomenti che
interessano la localizzazione subacquea.
-Il parametro accuratezza si riferisce alla precisione assoluta nella misurazione di un dato acustico.
-Il parametro risoluzione si riferisce alla capacità del sonar di discriminare tra due dati acustici.
-Il parametro precisione si riferisce alla finezza di misura del dato acustico.
Nella letteratura il tema è trattato in forma prevalentemente teorica nella quale la matematica statistica
svolge un ruolo preminente; cercheremo pertanto di svolgere la materia, per quanto possibile, secondo
semplici dimostrazioni tecniche.
Un sistema Sonar attivo è generalmente chiamato alle seguenti funzioni:
rivelazione dei bersagli, misurazione dei dati relativi ai vari bersagli rivelati in base
alle caratteristiche dei parametri acustici del sonar.
Queste operazioni debbono compiersi in presenza di rumore, che à essenzialmente di due tipi:
rumore (N) la cui potenza è funzione della banda (W) del ricevitore, e rumore (Rv) la cui potenza
è proporzionale all'energia dell'impulso trasmesso (riverberazione).
Del primo tipo sono il rumore acustico di fondo, dovuto ad esempio alla nave propria,
al moto ondoso di superficie, al movimento della nave nel mezzo, il rumore biologico e
quello elettronico strumentale.
Del secondo tipo di rumore sono la riverberazione di fondo, di superficie e di volume.
Possiamo quindi in generale parlare di disturbo D = N + Rv.
Nell'operazione di misurazione delle variabili acustiche intervengono i parametri di
accuratezza
risoluzione, e
precisione .
Se si osserva un parametro x, ad esempio la distanza o la velocità di un bersaglio, generalmente
il sistema risponderà per un dato valore x = xi con una funzione fi(x) di forma tale da presentare
un massimo per x = xi.
L' accuratezza con la quale si può stabilire il valore di x = xi per il quale la f(x) presenta
il massimo dipende dal rapporto S/D; quando infatti non vi fosse rumore presente, l'accuratezza sarebbe
quella intrinseca del sonar.
L'accuratezza dipende anche dalla durata dell'impulso f(x); a parità di rapporto S/D più breve
sarà tale impulso più precisi si potrà essere nello stabilire la sua posizione.
Se ad esempio con ΔR indichiamo il parametro d'accuratezza, ovvero l'errore massimo nella misura
della distanza R del bersaglio, questo sarà tanto più piccolo quanto la banda di ricezione sarà
larga; inversamente proporzionale alla banda del ricevitore.
Se vi sono simultaneamente due variabili acustiche Xi ed Xj da evidenziare, e se i due valori sono
sufficientemente lontani, vi sarà ben poca interazione tra le due risposte fi(X) ed fj(x), in quanto
generalmente i loro picchi laterali tendono ad attenuarsi rapidamente allontanandosi dal massimo.
Tale interazione dipenderà pure dal rapporto delle ampiezze delle due risposte. Quando le due ampiezze
sono uguali ed i due valori tendono ad avvicinarsi, si tenderà oltre un certo limite, a considerare
le due risposte come una sola. Il valore minimo della distanza Xj - Xi, per la quale sono ancora
distinguibili due distinti valori è determinato dalla risoluzione, o potere risolutore del
sistema nella variabile x.
Se ad esempio con Δφ indichiamo il parametro di risoluzione angolare, ovvero la differenza
angolare minima apprezzabile che separa due bersagli vicini, questa sarà inversamente proporzionale al rapporto
(lunghezza base ricevente / lunghezza d'onda); tanto più sarà lunga la base tanto più si
riuscirà ad apprezzare separatamente la posizione angolare tra due bersagli.
Nelle misure delle variabili acustiche indicate in 3) e 4) interviene sempre il parametro precisione che
ne consente il rilievo con una definizione strumentale, generalmente molto inferiore agli
altri parametri sonar, sia in angolo, sia in tempo che in frequenza.
Per l'esame del parametro accuratezza è più perspicua la sua illustrazione nel caso del rilevamento
angolare del bersaglio eseguito considerando la curva di direttività della base ricevente del sonar.
In questo caso il parametro accuratezza ha come simbolo Δα.
Una curva di direttività tipica è riportata in figura 1 nella quale si osserva la posizione ideale
del massimo in corrispondenza dell'ipotetico bersaglio per la direzione α0 = 50 °
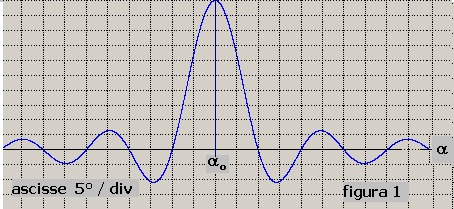
Nel caso specifico, non considerando il parametro precisione, ipotizziamo:
-disturbo: D = 0
-parametro di accuratezza del sonar: Δα = +/- 0.5°
ne segue che il bersaglio potrà essere rivelato con un'incertezza di +/- 0.5°; un qualsiasi valore
angolare compreso tra 49.5° e 50.5°.
Se il rilevamento del bersaglio si esegue in presenza del disturbo D la curva di direttività di
figura 1 la si può immaginare come indicato in figura 2 dove il disturbo altera la regolarità
della curva impedendo la collimazione precisa del massimo:
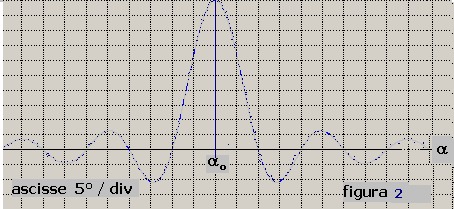
In questo caso il parametro di accuratezza indicato in precedenza con Δα = +/- 0.5° non
può essere applicato; si deve ricorrere ad un algoritmo particolare che tiene conto, sia delle caratteristiche
della curva di direttività teorica, sia del rapporto tra segnale S e disturbo D.
L'algoritmo citato, adattato per il sonar tra i diversi tipi utilizzati per la teoria dei radar, è
il seguente:
Δα = [0.354 θ √( 1 + S/D)] / [ (S/D) √(BxT) ]
dove:
θ = larghezza in gradi del lobo di direttività a -3dB
S/D = rapporto tra le potenze del segnale e del disturbo
B = banda di ricezione del sonar in Hz
T = tempo di durata dell'impulso in Sec.
Due esempi di calcolo riferiti ad un sonar avente la direttività indicata in figura 1:
primo: essendo θ = 10°; ipotizzando S/D = 1 (0 dB); B = 600 Hz; T = 0.01 Sec. si ha: Δα = 2°;
con Δα = 2° la misura della direzione potrà essere un qualsiasi valore compreso tra 48° e 52°.
secondo: essendo θ = 10°; ipotizzando S/D = 2 (3 dB); B = 600 Hz; T = 0.01 Sec. si ha: Δα = 1.20°;
con Δα = 1.20° la misura della direzione potrà essere un qualsiasi valore compreso tra 48.8° e 51.2°.
Come accennato in precedenza il parametro risoluzione si riferisce alla capacità del sonar
di discriminare tra due dati acustici; se questi sono afferenti alla direttività della base
del sonar il parametro risoluzione ha come simbolo: Δφ
Se ad esempio consideriamo i dati acustici relativi alle posizioni angolari di due bersagli, ciascuno
di essi sarà individuato da un diagramma di direttività così come mostra la figura 3, nella quale
il primo bersaglio (curva blu) è disposto su 30° e il secondo bersaglio (curva rossa) è disposto
su 50°.
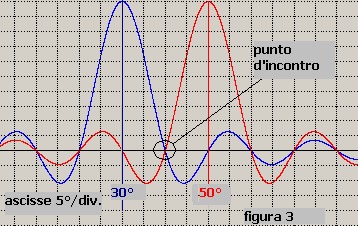
Il parametro di risoluzione del sonar, il cui limite vedremo in seguito, è definito dalle caratteristiche di direttività
tracciate in figura 3; queste nell'esempio specifico consentono le rilevazione dei due
bersagli senza possibilità assoluta di errore; questo perché la distanza angolare tra i due, di 20°, è il doppio
della larghezza dei singoli lobi misurata a -3 dB (10°); questa geometria fa sì che la somma Sm delle
tensioni s1 ed s2 dei due segnali nel punto d'incontro tra le due curve è irrilevante rispetto ai livelli
dei loro massimi.
Se i due bersagli sono più vicini, come ad esempio in figura 4, la possibilità di discriminare tra
le due posizioni angolari diventa più critica:
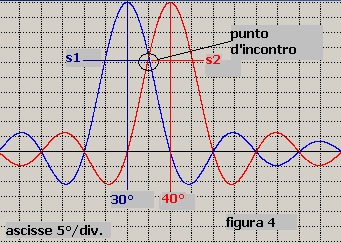
In questo caso infatti la somma Sm delle tensioni dei due segnali s1 = 0.6 ed s2 = 0.6 nel punto
d'incontro è pari a:
Sm = √ (s1 ² + s2 ²) = √ (0.6 ² + 0.6 ²) = 0.84
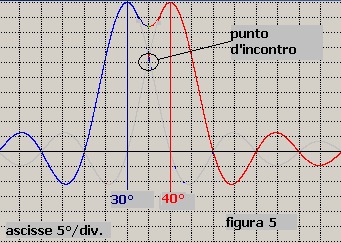
La presenza di Sm = 0.84 deforma il grafico di figura 4 in quello di figura 5 nel quale si vede
come le due curve, fondendosi in un'unica traccia, si differenzino meno angolarmente anche se
ancora in grado di discriminare le due diverse posizioni angolari a 30° e a 40°.
Quando la distanza angolare tra i due bersagli è 9° i valori di s1 e s2 sono pari a circa 0.7
così come mostra la figura 6:
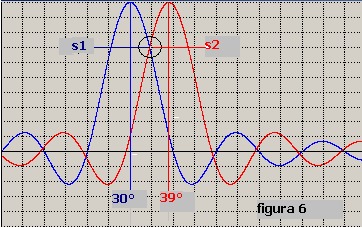
in questo caso la somma Sm è pari a:
Sm = √ (s1 ² + s2 ²) = √ (0.7 ² + 0.7 ²) = 0.94
e le due curve sono difficilmente discriminabili tra loro come si evince da figura 7:
La figura mostra che la discriminazione tra i due bersagli non è più possibile; s'individua un solo falso bersaglio
per la direzione mediana, nel nostro caso per circa 35°.
Si deduce quindi che il limite del parametro di risoluzione angolare ( Δφ ),
essendo uguale a 10°, corrisponde alla larghezza del lobo a -3dB della curva di figura 1.
Concludendo possiamo infine scrivere che, con buona approssimazione, la risoluzione angolare è
identificabile con la larghezza, a -3dB, del lobo di direttività; ovvero: Δφ = θ.
Per l'esame del parametro precisione è più semplice la sua illustrazione nel caso della misura
della distanza R di un bersaglio illuminato dall'impulso del sonar.
In questo caso il parametro precisione viene definito con il simbolo ΔR.
Supponiamo ora che il sonar riceva l'eco del bersaglio da una distanza R = 8750 m e che il misuratore
della distanza, di tipo digitale, abbia una precisione ΔR = 100 m ;
il risultato della misura, indipendentemente dall'attendibilità del valore di R legata all'accuratezza
del sistema, potrà indicare una distanza R di 8700 m o di 8800 m.