Geometria analitica (25°)
Relazioni tra iperbole traslata e rette tangenti

1)Generalità
Per venire incontro a numerose richieste per l'estensione dei file eseguibili, dei tipi già utilizzati in p55 e p57, per la soluzione di altri problemi di geometria analitica, si illustrano alcune routine di calcolo per la soluzione di casi diversi che possono essere utili a chi deve cimentarsi in questa interessante parte della matematica.
Una premessa è necessaria prima del prosieguo della pagina: gli algoritmi utilizzati non sono dimostrati ma soltanto implementati, a favore del calcolo automatico, in apposite routine in Visual Basic; per le dimostrazioni si rimanda agli innumerevoli testi di geometria analitica in commercio.

2)Le scelte di calcolo
Il calcolo dell'equazioni delle rette tangenti ad un'iperbole traslata, rette passanti per un punto p(x1; y1) esterno all'iperbole, presuppongono la soluzione del seguente sistema:
A X² + B Y² + C X + D Y + E = 0
Y = m X - m x1 + y1
e la conseguente soluzione dell'equazione in m dovuta all'imposizione del discriminante nullo:
Δ = 0
Il problema accennato presenta notevoli difficoltà non facilmente superabili; un diverso approccio per la sua soluzione è stato sviluppato in questa pagina secondo la procedura che indichiamo di seguito:

-1) con i coefficienti A; B; C; D; E dell'iperbole traslata se ne determinano le coordinate Xo: Yo del centro

-2) con le coordinate Xo: Yo e i coefficienti dell'iperbole traslata si calcola l'equazione di una nuova iperbole (iperbole base), discendente dalla prima, con il centro nell'origine degli assi:
X² / a² - Y² / b² = 1

-3) si calcolano l'equazioni delle tangenti alla nuova iperbole, passanti per p(x1; y1) mediante la soluzione del sistema:
X² / a² - Y² / b² = 1
Y = m X - m x1 + y1
ottenibile tramite il metodo dello sdoppiamento

-4)si esegue infine la traslazione dell'equazioni delle tangenti così calcolate, con riferimento al sistema di assi cartesiani con centro x = 0; y = 0, al sistema di assi cartesiani con centro Xo; Yo.

3)Algoritmi in V.B. per le relazioni tra iperbole traslata e rette tangenti
In questa pagina è riportato un file eseguibile che consente, in modo rapido, la formulazione dell'equazioni e il tracciamento delle rette tangenti alla conica definita dall'equazione:
A X² + B Y² + C X + D Y + E = 0 (iperbole traslata)
Il programma calcola e traccia:
1-la conica e le coordinate del centro e dei fuochi della stessa
2-l'equazioni delle rette tangenti passanti per x1; y1
3-le coordinate dei punti di contatto tra tangenti e conica

Gli algoritmi implementati, scritti in linguaggio V.B. sono:

-dati d'ingresso:
Akk; Bkk; Cck, Ddk; Eek (coeff. della conica)
x1; y1 coordinate del punto di passaggio delle rette (esterno alla conica)

-trasformazioni per la costruzione della conica di base:
Uu1 = Akk
Vv1 = -Bkk
aa1 = Sqr(1 / Uu1)
bb1 = Sqr(1 / Vv1)

-calcolo coordinate del centro e del fuoco dell'iperbole traslata:
xo = -Cck / (2 * Uu1)
yo = Ddk / (2 * Vv1)
cc1 = Sqr(bb1 ^ 2 + aa1 ^ 2) + xo
cc2 = Sqr(bb1 ^ 2 + aa1 ^ 2) - xo

-calcolo elementi per il grafico dell'iperbole traslata
kk2 = -2 * yo * Vv1
Kk1 = Uu1 * x ^ 2 - 2 * Uu1 * x * xo + Uu1 * xo ^ 2 + Vv1 * yo ^ 2 - 1
ytt1 = (-kk2 + Sqr(Abs(kk2 ^ 2 - 4 * Vv1 * Kk1))) / (2 * Vv1)
ytt2 = (-kk2 - Sqr(Abs(kk2 ^ 2 - 4 * Vv1 * Kk1))) / (2 * Vv1)
kk2 = -2 * yo * Vv1
Kk1 = Uu1 * x ^ 2 - 2 * Uu1 * x * xo + Uu1 * xo ^ 2 + Vv1 * yo ^ 2 - 1
ytt3 = (-kk2 + Sqr(Abs(kk2 ^ 2 - 4 * Vv1 * Kk1))) / (2 * Vv1)
ytt4 = (-kk2 - Sqr(Abs(kk2 ^ 2 - 4 * Vv1 * Kk1))) / (2 * Vv1)

-struttura per il calcolo e il tracciamento delle tangenti:
xop = x1 - xo
yop = y1 - yo
k1 = aa1 ^ 2 * bb1 ^ 2
k2 = aa1 ^ 2 * yop
k3 = bb1 ^ 2 * xop
A1 = bb1 ^ 2 * k2 ^ 2 - aa1 ^ 2 * k3 ^ 2
B1 = 2 * bb1 ^ 2 * k1 * k2
c1 = bb1 ^ 2 * k1 ^ 2 - k1 * k3 ^ 2
Y1 = (-B1 + Sqr(B1 ^ 2 - 4 * A1 * c1)) / (2 * A1)
X1 = (k1 + k2 * Y1) / k3
Y2 = (-B1 - Sqr(B1 ^ 2 - 4 * A1 * c1)) / (2 * A1)
X2 = (k1 + k2 * Y2) / k3
m = (Y1 - yop) / (X1 - xop)
n = -m * (xop + xo) + yop + yo
yt1 = m * x + n
m1 = (Y2 - yop) / (X2 - xop)
n1 = -m1 * (xop + xo) + yop + yo
yt11 = m1 * x + n1

-calcolo delle coordinate dei punti di contatto
xtan = -(2 * Bkk * m * n + Cck + Ddk * m) / (2 * (Akk + Bkk * m ^ 2))
ytan = m * xtan + n
xtan1 = -(2 * Bkk * m1 * n1 + Cck + Ddk * m1) / (2 * (Akk + Bkk * m1 ^ 2))
ytan1 = m1 * xtan1 + n1

4)L'impiego del file eseguibile
Il file eseguibile, al lancio sul P.C, si presenta come mostrato in figura 1, in essa s'individuano il tracciato cartesiano e 8 caselle d'immissione dati con un pulsante d'avvio "Calcolo" e un CheckBox di consenso.
Nel reticolo cartesiano saranno tracciati:
-i due rami dell'iperbole traslata (colore blu)
-le due rette tangenti (colori rosso e nero)
Nelle 5 caselle "A" .... "E" si devono digitare i valori dei coefficienti dell'iperbole traslata.
Nelle caselle "x1" ; "y1" si devono digitare i valori delle coordinate del punto di passaggio delle tangenti, esterno all'iperbole.
A fianco di queste il Check che abilita il calcolo delle tangenti.
Nella casella "Scala" il valore da assegnare al fondo scala del reticolo affinché possa contenere il tracciato completo della conica e delle tangenti
Nella parte alta dello schermo saranno presentate l'equazioni esplicite delle rette tangenti e le coordinate dei punti di tangenza.
Nella parte bassa dello schermo saranno presentate in forma numerica le coordinate del centro ed il fuoco dell'iperbole traslata in fase di studio.
Le 8 caselle contengono una serie di dati per il primo approccio alla schermata di calcolo; questi sono tutti modificabili su digitazione da tastiera.

4)Esempio d'utilizzo del programma di calcolo
In questo paragrafo viene proposto un esercizio grafico numerico la cui risoluzione è basata sul file eseguibile (eserc.iptratg) .
Una volta lanciato l'eseguibile la schermata è quella già mostrata in figura 1, pigiando il pulsante calcolo viene tracciata in blu l'iperbole, i cui coefficienti sono già presenti nelle caselle d'immissione dati, si evidenzia inoltre, in verde, il punto p(x1; y1) esterno all'iperbole, in questo caso al centro degli assi cartesiani, si veda figura 2:



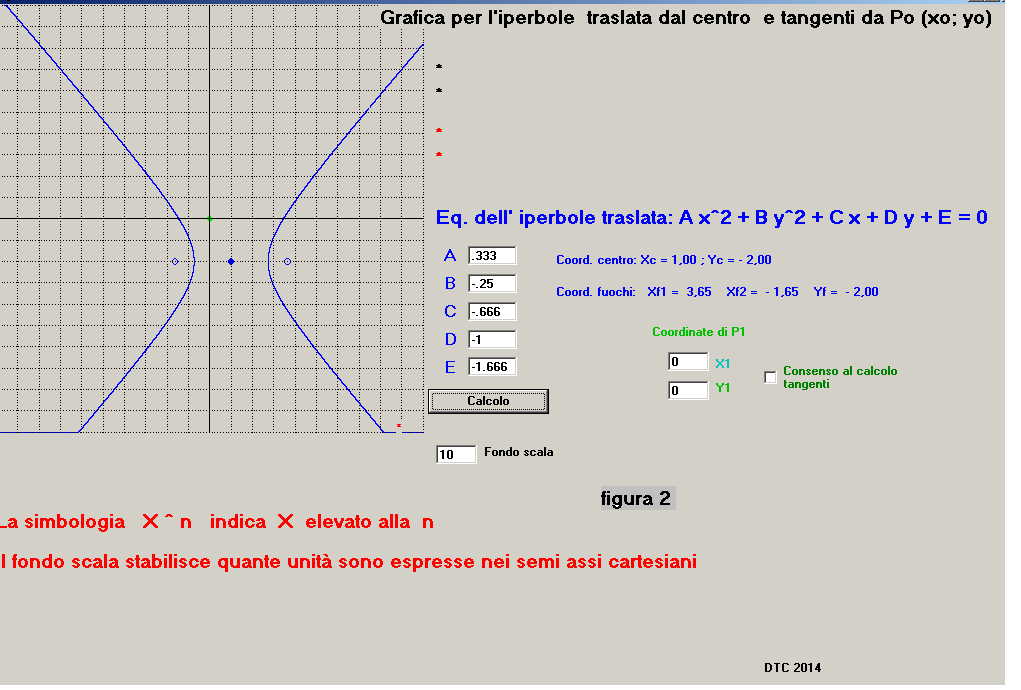
A questo punto, visto che p(x1; y1) è esterno all'iperbole, si consente il calcolo delle tangenti predisponendo il Check di consenso all'operazione, si pigia di seguito ancora il pulsante calcolo e si ottiene la schermata completa delle rette tangenti con relative equazioni esplicite, si veda figura 3:



La procedura d'impiego indicata consente il controllo a priori della validità del calcolo mostrando che la posizione del punto di passaggio delle tangenti è esterna all'iperbole; in generale una volta stabilite le coordinate del punto in oggetto se questo è esterno al grafico dell'iperbole data è possibile attivare il consenso al calcolo delle tangenti, se il punto non è esterno all'iperbole il consenso non deve essere dato; se non si rispetta tale procedura l'eseguibile si blocca e si deve ripetere il lancio del programma.

Eseguiamo ora un esercizio di calcolo delle tangenti ad un'iperbole traslata di equazione:
0.6 X² - 0.5 Y² + 2 X - 5 Y - 1 = 0
le tangenti devono passare per il punto p( x1 = - 1.5 : y1 = 2 )
Si digitano nelle caselle dei coefficienti i nuovi dati, in sostituzione degli esistenti al lancio:
A = + 0.6
B = - 0.5
C = + 2
D = - 5
E = - 1
e le coordinate di p: x1 = - 1.5 e y1 = 2
Si preme il pulsante calcolo e si ottiene la schermata di figura 4 nella quale abbiamo evidenziato i punti caratteristici:
p1 (verde) punto di passaggio rette tangenti (esterno all'iperbole)
po (blu) centro della conica
f1, f2 fuochi della conica:



Constatato che il punto p1 è all'esterno della conica si può abilitare il calcolo delle tangenti ottenendo infine la schermata risolutiva del problema come mostrato in figura 5



nella quale leggiamo:
coordinate del centro iperbole:( xc = -1.67 ; yc = - 5)
coordinate dei fuochi iperbole: (f1 = 0.25 ; -5 ) (f2 = -3.58 ; -5)

equazione tangente nera: y = -6.34 x - 7.5
coordinate punto di tangenza nero pt1(xt1 = - 0.36 ; yt1 = - 5.25)

equazione tangente rossa : y = 4.91 x + 9.37
coordinate punto di tangenza rosso pt2(xt2 = - 2.99 ; yt2 = - 5.32)

5)Note
-Generalmente i problemi scolastici di geometria analitica mostrano, in tutti i casi, l'impiego di numeri razionali (frazioni numeriche) o irrazionali (radici quadrate) per l'eleganza formale del testo; è naturale quindi che per il controllo dei risultati di un problema di tipo scolastico con l'analogo sviluppato con le nostre routine si dovranno trasformare i valori razionali o irrazionali esposti per il primo in valori decimali per il confronto con il secondo.

-Il controllo software del file eseguibile è stato eseguito al meglio; è possibile però che qualche particolare anomalia sia sfuggita all'esame.
Si prega pertanto chi dovesse riscontrare qualche difetto nell'impiego del programma di renderlo noto tramite " Contatti con l'autore"; si provvederà all'aggiustaggio in rete.