SONAR-INFO-p120
CORRELATORI E RIVELATORI
-Analisi delle differenze-
1) Generalità 2) Correlatore e rivelatore sul dipolo 2.1) Caratteristiche dinamiche di un correlatore collegato ad un dipolo 2.2) Caratteristiche dinamiche di un rivelatore collegato ad un dipolo 2.3) Caratteristica di direttività di un dipolo in correlazione 2.4) Caratteristica di direttività di un dipolo su rivelatore 2.5) Analisi delle differenze tra correlazione e rivelazione sul dipolo 3) Correlatore e rivelatore su base a 8 idrofoni Di notevole interesse è l'esame dei due metodi di detezione del segnale,
illustrati in precedenza, quando questi sono applicati ad una base idrofonica con un numero
considerevole di sensori idrofonici.
3.1) Caratteristica di direttività di una base a 8 idrofoni su rivelatore 3.2) Caratteristica di direttività di una base a 8 idrofoni in correlazione 3.3) Analisi delle differenze tra correlazione e rivelazione su base a più idrofoni 4) Cenni sulla tecnica di compensazione del rumore
Chiudiamo questa pagina facendo cenno alla tecnica di compensazione del rumore
sui rivelatori; tecnica che minimizza la presenza della componente continua della quale abbiamo
trattato in precedenza ( vedi paragrafo 2.2 ).
4.1) Sulla compensazione del rumore all'uscita dei rivelatori
L'argomento riportato nella presente pagina, già in parte trattato in p5 / cap 9 / par. 9.13, rappresenta
un'estensione significativa di quello sviluppato nella pagina citata.
L'analisi delle differenze funzionali esistenti tra correlatori e rivelatori
è di fondamentale importanza nella scoperta dei segnali idrofonici che sono inquinati dai disturbi.
Individuare le ragioni per le quali un dispositivo consente di ottenere un migliore differenziale
di riconoscimento dell'altro aiuta nella scelta tra i due sulla base delle esigenze del progetto
generale del sonar.
I dispositivi citati sono ugualmente realizzabili, con le caratteristiche che illustreremo, sia
con tecniche hardware che con processi esclusivamente software.
Forti delle indicazioni esposte in p5 prendiamo in esame un correlatore del tipo a coincidenza
di polarità che ben si presta per la scoperta sonar.
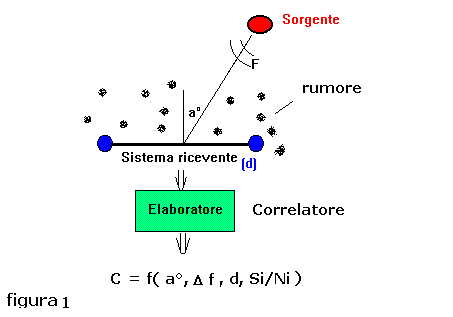
Ipotizzando uno scenario subacqueo simile a quello riportato in figura 1, una volta applicate le tensioni
idrofoniche generate dai due sensori ai due ingressi del correlatore, abbiamo all'uscita dello stesso
un livello di correlazione la cui ampiezza varia secondo la funzione di più variabili:
C = f( a°, Si/Ni, d, Δf )
dove:
a° = angolo di provenienza dell'onda acustica rispetto al traverso del dipolo
Si/Ni = rapporto tra il segnale ed il disturbo
d = lunghezza del dipolo
Δf = banda delle frequenze ricevute
Se supponiamo a° = 0; d = costante; Δf = costante si può scrivere:
C = f(Si/Ni)
Questa è la caratteristica esenziale del dispositivo citato che mostra come
varia l'ampiezza della sua uscita "funzione di correlazione" al variare del rapporto tra i segnali
Si ed i rumori Ni ai suoi due ingressi quando i due segnali Si siano coerenti tra loro (caso per a° = 0).
la funzione C = f( Si/Ni ) è definita secondo l'espressione:
L'andamento della funzione indicata è riportato in figura 2; in essa la variabile Si/Ni è
espressa in dB in un campo di variabilità compreso tra -20 dB e + 20 dB :
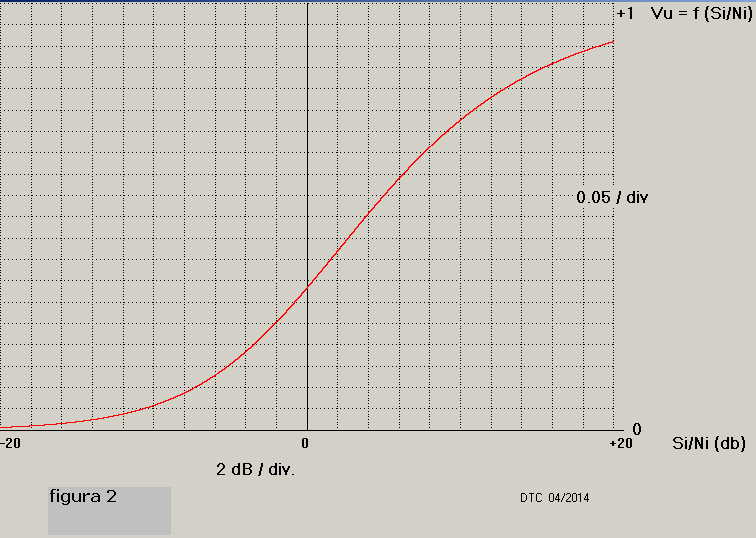
La curva mostra che, inequivocabilmente, esiste sempre una sola coppia di valori,
(Si/Ni) in dB e
C = f( Si/Ni ) in tensione continua, che indica la presenza del segnale Si individuato dal correlatore;
ovvero se all'uscita del dispositivo si genera un livello continuo di tensione è indubbia la presenza del segnale Si.
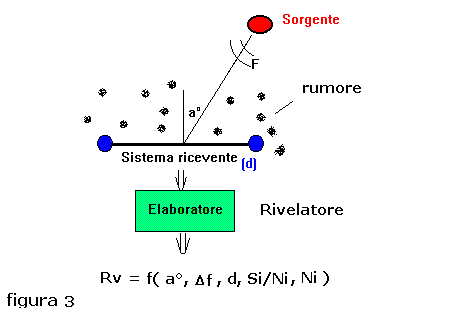
Ipotizzando uno scenario subacqueo simile a quello riportato in figura 3, nel quale le due tensioni
idrofoniche all'uscita dei sensori sono prima sommate tra loro e quindi applicate al rivelatore,
all'uscita dell'elaboratore abbiamo il livello di tensione che varia secondo la funzione di più
variabili:
Rv = f( a°, Si/Ni, d, Δf, Ni)
dove:
a° = angolo di provenienza dell'onda acustica rispetto al traverso del dipolo
Si/Ni = rapporto tra il segnale ed il disturbo
Ni = rumore ricevuto
d = lunghezza del dipolo
Δf = banda delle frequenze ricevute
Se supponiamo a° = 0; d = costante; Δf = costante si può scrivere:
Rv = f(Si/Ni, Ni)
Questa è la caratteristica del dispositivo citato che mostra come varia l'ampiezza della sua uscita
"Rv" al variare del rapporto Si/Ni e del rumore Ni.
L'andamento dell'ampiezza della tensione Rv all'uscita del rivelatore in dipendenza del rapporto Si/Ni d'ingresso,
e del rumore Ni è espresso da una funzione parametrica in Ni.
Rv = Ni [ 1.41 + 2 * 10^(sn/20)]
dove sn è il rapporto Si/Ni espresso in dB.
E' chiaro quindi che innumerevoli curve di Rv possono essere tracciate in funzione di Si/Ni al
variare del parametro Ni così come mostrano la serie di tracciati riportati in figura 4 per:
Ni= 0.01; Ni= 0.02; Ni= 0.04; Ni= 0.08 ;
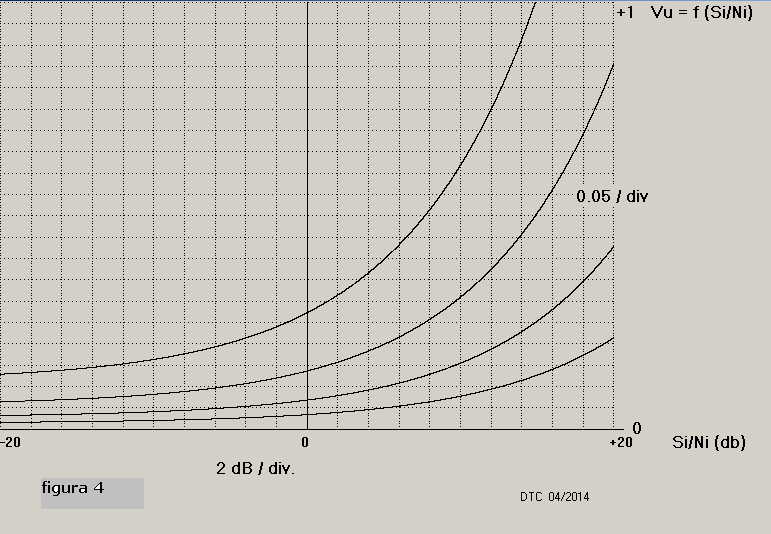
La serie di curve mostra che l'ampiezza di Rv all'uscita del rivelatore non indica con certezza
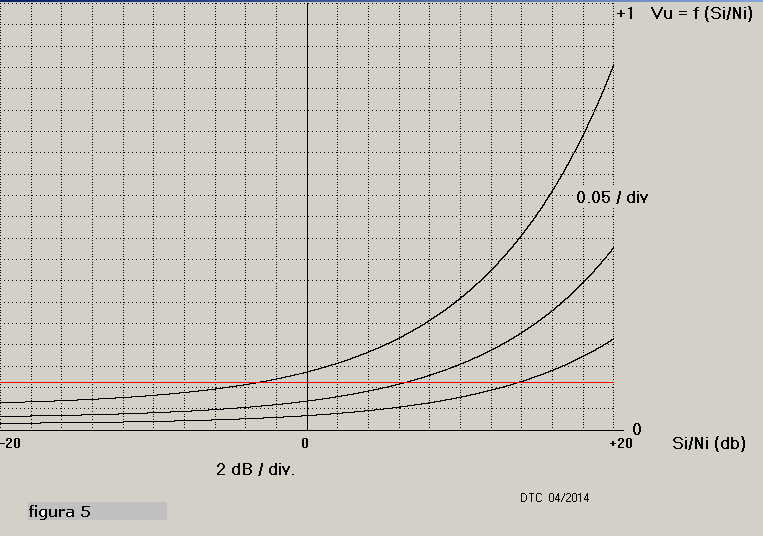
la presenza di un segnale Si dato che la sola presenza di Ni, in assenza assoluta del
segnale, può generare un certo livello di Rv cosi come mostra la figura 5 nella quale sono
ripetute le curve di figura 4 con la sostituzione del tracciato per Ni = 0.08 e Si/Ni variabile
con il tracciato rosso con Ni = 0.08 e Si/Ni = 0 .
La caratteristica di direttività del dipolo di figura 1 ottenuta mediante la correlazione ha
ancora la funzione implicita mostrata in precedenza:
C = f( a°, Si/Ni, d, Δf ) per la quale:
assumendo : a° = variabile, Si/Ni = ∞, d = costante; Δf = costante.
si può scrivere:
C = f( a° )
La funzione esplicita di C = f( a° ) è:
L'andamento della funzione illustrata per:
a = variabile da -20° a + 20°
F1 = 1500 Hz
F2= 3000 Hz
d = 4.8 m
è riportato in figura 6:
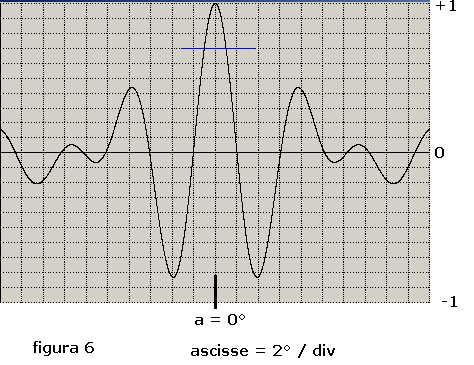
Dalla figura si evince:
1) il massimo della caratteristica di direttività del dipolo si ottiene per a = 0°, condizione di sorgente al traverso.
2) la larghezza del lobo di direttività, misurata a - 3dB sotto il massimo, ha un'ampiezza di 2°
3) il livello dei primi avallamenti adiacenti a massimo ad un valore di 21 dB sotto il massimo
4) il livello dei lobi secondari è 7 dB sotto il massimo
5) per direzioni molto lontane dal traverso la funzione ondula e tende a livello 0
La caratteristica di direttività del dipolo di figura 3, ottenuta mediante il rivelatore,
ha ancora la funzione implicita mostrata in precedenza:
Rv = f( a°, Si/Ni, d, Δf, Ni)
assumendo : a° = variabile, Ni = 0, d = costante; Δf = costante.
si può scrivere:
Rv = f( a° )
La funzione esplicita di Rv = f( a° ) è:
L'andamento della funzione illustrata per:
a = variabile da -20° a + 20°
f1 = 1500 Hz
f2 = 2 f1
d = 4.8 m
è riportato in figura 7:
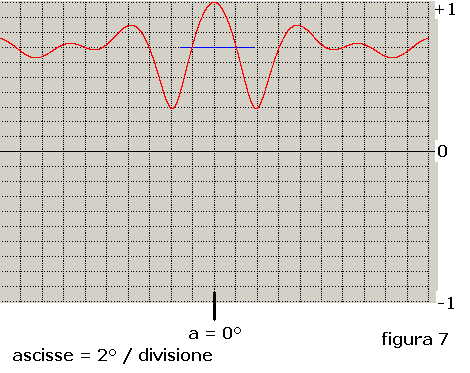
Dalla figura si evince:
1) il massimo della caratteristica di direttività del dipolo si ottiene per a = 0°, condizione di sorgente al traverso.
2) la larghezza del lobo di direttività, misurata a - 3dB sotto il massimo, ha un'ampiezza di 4°
3) il livello dei primi avallamenti adiacenti a massimo è di 10 dB sotto il massimo
4) il livello dei lobi secondari è 1.4 dB sotto il massimo
5) per direzioni molto lontane dal traverso la funzione ondula e tende a livello 0.7
Il dipolo, a causa della sua semplice struttura, evidenzia al massimo le differenze della correlazione
rispetto alla rivelazione:
A) La prima e fondamentale differenza tra i due metodi di scoperta del segnale è relativa alla
larghezza del lobo di direttività che per la correlazione risulta circa la metà rispetto alla
rivelazione; questa caratteristica peculiare dei metodi di correlazione resta immutata per
qualsiasi configurazione della base acustica, dal dipolo alle cortine con molti sensori idrofonici.
B) La presenza degli avallamenti attorno al massimo, utile per individuare meglio la
sorgente acustica, è indubbiamente a favore del correlatore ma, come
vedremo più avanti, per basi a più idrofoni i due livelli si avvicinano riducendo le differenze.
C) I livelli dei lobi secondari attorno al massimo, che possono creare ambiguità nella scoperta del bersaglio,
sono indubbiamente a favore del correlatore, ma per basi a più idrofoni i due livelli si avvicinano
riducendo le differenze.
D) La differenza tra i livelli d'uscita tra i due sistemi di scoperta per direzioni molto lontane
dal traverso è naturalmente a favore del correlatore che vede il livello d'uscita azzerarsi,
contrariamente al livello del rivelatore che resta elevato; questa differenza sostanziale resta, a
livelli inferiori, in dipendenza del numero dei sensori idrofonici della base.
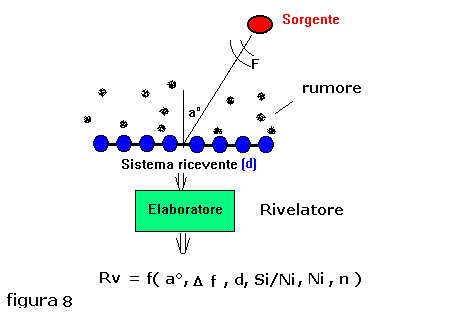
La caratteristica di direttività della base idrofonica indicata in figura 8 , ottenuta mediante
rivelazione ,ha ancora la funzione implicita mostrata in precedenza con la comparsa della variabile
"n" che indica il numero dei sensori che formano la base:
Rv = f( a°, Si/Ni, d, n, Δf, Ni)
La funzione esplicita di Rv, studiata da Stenzel, è sotto riportata:

Il valore di Rv si concretizza collegando all'ingresso del rivelatore la somma di tutti gli 8
segnali provenienti dagli idrofoni della base.
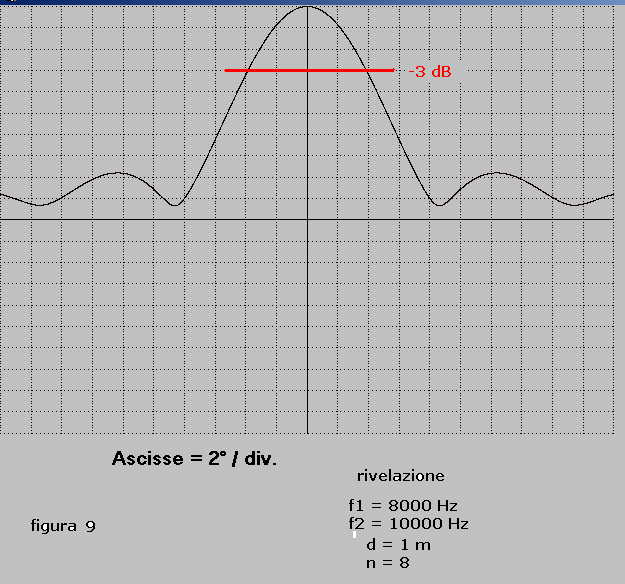
In figura 9 è tracciata la caratteristica di direttivita su rivelatore calcolata per le seguenti
variabili:
d = 1 m
n = 8
f1 = 8000 Hz
f2 = 10000 Hz
a = variabile da -20° a + 20°
La caratteristica di direttività della base idrofonica indicata in figura 10 , ottenuta mediante
correlazione, ha ancora la funzione implicita mostrata in precedenza con la comparsa della variabile
"n" che indica il numero dei sensori che formano la base:
C = f( a°, Si/Ni, d, Δf, n )

La funzione esplicita di C, studiata per il sonar FALCON, è sotto riportata: (si veda "studio FALCON" in p 4)

Il valore di C si concretizza collegando all'ingresso dei 4 correlatori le 4 coppie dei
segnali provenienti dagli idrofoni della base.
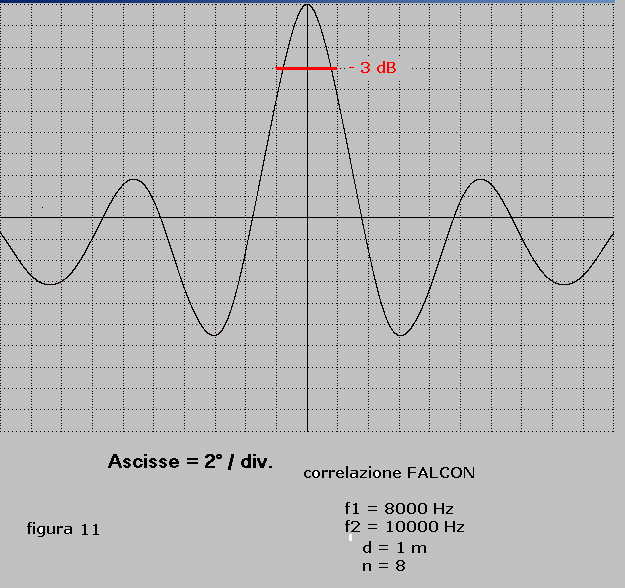
In figura 11 è tracciata la caratteristica di direttività in correlazione FALCON calcolata
per le seguenti variabili:
d = 1 m
n = 8
f1 = 8000 Hz
f2 = 10000 Hz
a = variabile da -20° a + 20°
A) La prima e fondamentale differenza tra i due metodi di scoperta del segnale è relativa alla
larghezza del lobo di direttività che per la correlazione risulta circa la metà rispetto alla
rivelazione; questa peculiarità è utile per ottenere migliori precisioni di scoperta ma al prezzo
del raddoppiamento dei fasci preformati per la ricerca dei bersagli.
B) La presenza degli avallamenti attorno al massimo, utile per individuare meglio la
sorgente acustica, è sensibilmente a favore del correlatore.
C) I livelli dei lobi secondari attorno al massimo, che possono creare ambiguità nella scoperta
del bersaglio, sono praticamente agli stessi.
D) La differenza tra i livelli d'uscita tra i due sistemi di scoperta per direzioni molto lontane
dal traverso è naturalmente a favore del correlatore che vede il livello d'uscita azzerarsi,
contrariamente al livello del rivelatore che resta elevato; detto livello esprimibile per il
dipolo con il rapporto √: 2 / 2 = 0.7. (rispetto al massimo) è nel caso di base a 8 elementi
pari a: √: 8 / 8 = 0.28 (rispetto al massimo).
E) Il comportamento del rivelatore al rumore Ni, evidenziato per il dipolo al paragrafo 2.2, resta
tale, anche se a livelli inferiori, per le basi a più idrofoni.
Il metodo, applicabile soltanto se la scoperta sonar è affidata ad un sistema di fasci preformati,
si avvale della computazione del rumore medio, Nm, presente sui detti fasci per tutti i 360° dell'orizzonte,
che, se il bersaglio è lontano, viene assunto come parametro base da sottrarre al parametro Ni della funzione:
Rv = f( a°, Si/Ni, d, Δf, Ni)
che diventa:
Rv = f( a°, Si/Ni, d, Δf, Ni-Nm ).
L' argomento è affrontato, in termini probabilistici, nella pagina 122.