SONAR-INFO-p124
RIVELATORI QUADRATICI
-Analisi del comportamento sul segnale e rumore-
1) Generalità 2) Analisi di un rivelatore quadratico con segnale e disturbo all'ingresso 3) Analisi di un rivelatore quadratico al variare del rapporto S/N d'ingresso P(riv) = 0.5[1 + erf(x)]
In p122 abbiamo esaminato il comportamento del rivelatore quadratico nel caso in cui al suo
ingresso sia presente soltanto rumore perturbante, nella presente pagina indaghiamo sul comportamento
del dispositivo quando al suo ingresso siano presenti, contemporaneamente, sia rumore che segnale.
Anche per queste considerazioni ci serviremo del metodo statistico.
Nella rivelazione quadratica quando all'ingresso è presente sia segnale che rumore perturbante
in banda 2Δf, all'uscita U, dopo l'integratore, si ha:
-una componente continua di ampiezza ( S + N ) dovuta alla somma delle potenze di segnale e di rumore
-una componente alternata di valore efficace (deviazione standard) δn = ( S + N ) / √( 4 RC Δf )
dove RC è la costante di tempo dell'integratore.
Se ad esempio assumiamo, come in p122, RC = 1 Sec; Δf = 4000 Hz si ha:
δn = ( S + N ) / 126.5
Supponiamo ora che all'uscita dell'integratore post rivelazione siano impostati sempre lo stesso
livello di soglia T = 0.12N e lo stesso livello di compensazione 0.1N già calcolati in p122, e
che il segnale raggiunta la soglia T possa garantire, al minimo, una probabilità di scoperta pari a P(riv) = 50 % così come mostra la curva
probabilistica di figura 1
( naturalmente sempre in presenza di P(fa) = 10 % ):
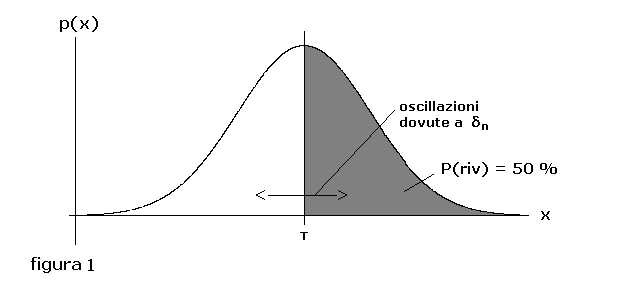
In tal caso il livello So del segnale avrà un'ampiezza pari a T ovvero So = T = 0.12N ; dato
che per il rumore abbiamo un'ampiezza pari ad N il rapporto segnale disturbo sarà:
S / N = 0.12 N / N = 0.12
che espresso in decibel è: (S/N)dB = 10 log 0.12 = - 9.2 dB
Il computo della probabilità di rivelazione P(riv), secondo la formula classica è:
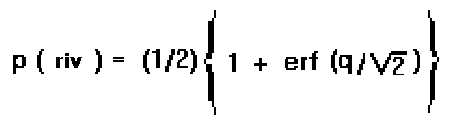
Per verificare che la probabilità di scoperta P(riv) sia pari al 50% si considerano:
-le variabili date: [ S/N = -9.2 dB; T = 0.12N; So = 0.12N; δn = ( S + N ) / 126.5 ]
-la differenza q tra il livello di T ed So normalizzata su δn ; q = ( T - So ) / δn = 0
- l'argomento x della funzione errore x = q / √2 = 0; che genera erf(0) = 0
- la formula sopra riportata che esplicita: P(riv) = .5 ( 1 + 0 ) = 0.5 ; (pari al 50%)
Lavorando con i valori e le formule del paragrafo 2 è possibile stabilire come varia la probabilità
di rivelazione P(riv) al variare del rapporto S/N all'ingresso del rivelatore.
Supponiamo ora che S/N s'incrementi, fermo restando il valore di N assunto al livello N = 1, a
seguito dell'incremento di S, da So = 0.12 , a valori Si > So possiamo scrivere:
qi = ( T - Si ) / δn
per S/N crescente, diventando Si > T, si scrive:
qi = ( Si - T ) / δn = (Si - 0.12N) / [( Si + N ) / 126.5] = 126.5 (Si - 0.12) / ( Si + 1 )
Una tabella di P(riv) in funzione di (S/N)dB è sotto riportata per S/N variabile da -9.2 dB
a -8.86 dB;
la determinazione della funzione d'errore erf(x), per i diversi valori di x, si ottiene o
tramite l'uso di tabelle, ad esempio su "HANDBOOK OF MATHEMATICAL FUNCTION" di Abramowitz and
Stegun o tramite lo sviluppo dell'integrale:
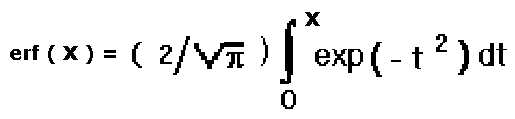
S/N(dB)
Si
x = [(Si - T) / δn] / 1.41
erf(x)
-9.20
0.120
0.00
0.00
0.50
-9.17
0.121
0.08
0.056
0.54
-9.13
0.122
0.16
0.113
0.59
-9.10
0.123
0.24
0.26
0.63
-9.06
0.124
0.32
0.35
0.67
-9.03
0.125
0.40
0.43
0.71
-8.99
0.126
0.48
0.50
0.75
-8.96
0.127
0.55
0.56
0.78
-8.93
0.128
0.63
0.63
0.81
-8.89
0.129
0.71
0.68
0.84
-8.86
0.130
0.79
0.74
0.87
Dalla tabella si evince che per un incremento di (S/N) di soli 0.34 dB, da (-9.2 dB) a (- 8.86 dB)
la probabilità di scoperta varì dal 50 % all'87 %.
Ciò, ad esempio, può alterare le caratteristiche di un insieme di M fasci preformati
dato che sarà sufficiente una piccola differenza del rapporto S/N tra gli M canali per
diversificarne la loro caratteristica percentuale di rivelazione P(riv) e far sì che la distanza di
scoperta dei bersagli vari con la direzione.