1) Generalità
La funzione RLI del sonar (Right Left Indicator), il sistema che indica i piccoli spostamenti angolari del bersaglio, è stata sviluppata in diversi modi, tra questi con i sistemi di correlazione grazie all'impiego della trasformata di Hilbert.
In questa pagina mostreremo come la funzione di correlazione si modifica nelle trasformata di Hilbert e quali differenze e vantaggi derivano da quest'ultima.

2) La funzione di correlazione con segnali limitati
La funzione di correlazione di cui al titolo risponde al noto algoritmo:

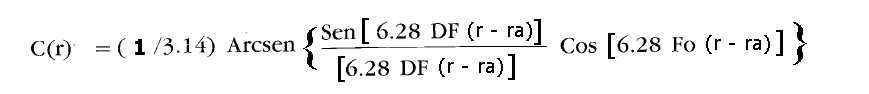1)

dove:
Fo = ( F1 + F2 ) / 2
DF = (F2 - F1 ) / 2
F1 = frequenza inferiore della banda di ricezione; in Hz
F2 = frequenza superiore della banda di ricezione; in Hz
r = variabile indipendente; in Sec.
ra = d Sen( a° ) / 1530 ; ritardo dell'onda dovuto alla posizione angolare del bersaglio.
a° = angolo di puntamento del bersaglio; in gradi
d = lunghezza della base; in m.

Se ad esempio la base idrofonica ricevente e la sorgente acustica sono disposti secondo la figura 1,
con d = 1.35 m, la funzione di correlazione darà il suo massimo, in corrispondenza del valore di r pari a:
r = ra = d Sen( 27° ) / 1530 in Sec = 400 μ Sec.
La C(r) presenterà quindi il livello più elevato per la direzione a = 27°.



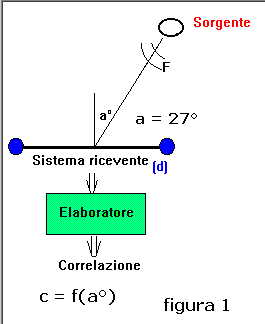
L'andamento di C(r), per F1 = 2000 Hz e F2 = 10000 Hz, ed a = 27°, è riportato in figura 2 per r variabile da 0 a 1000 μ Sec.



Una volta puntata la sorgente per a = 27° il livello della funzione decrescerà se la sorgente stessa si sposterà in più od in meno rispetto al valore di 27°: ad esempio per uno scostamento da 27° di +/- 0.5 ° il ritardo ra varierà di circa +/- 7 μSec. generando un decremento del livello di C(r) dell'ordine del 14 %: questa indicazione d'allerta non consente però di stabilire se la variazione della posizione angolare del bersaglio è dovuta ad una contromanovra a destra o a sinistra dato che C(r), essendo una funzione pari, decresce sia quando l'angolo "a" cresce sia quando diminuisce.
La trasformazione della C(r) da funzione pari a funzione dispari è fattibile grazie alla trasformata di Hilbert; con essa è possibile la discriminazione del senso delle contromanovre del bersaglio così come illustrato di seguito.

3) La trasformata di Hilbert
La trasformata di Hilbert, indicata come HC(r), si genera quando i segnali all'ingresso di un correlatore digitale sono sfasati di 90° a tutte le frequenze che ne compongono lo spettro.
Da un punto di vista tecnico lo sfasamento richiesto è realizzabile ma non facilmente, in special modo per bande di frequenze estese; sono state studiate diverse procedure sia hardware che software per risolvere il problema del quale, peraltro, non ci cimentiamo in questa pagina limitandoci all'impiego del concetto nell'ambito della stesura delle formule della HC(r).

Lo schema a blocchi per la realizzazione della HC(r) è riportato in figura 3



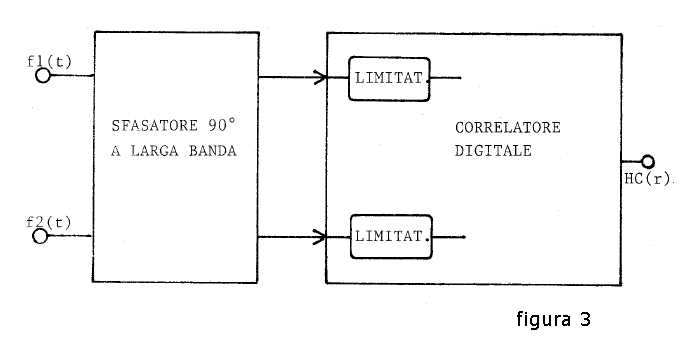
dove con f1(t) e f2(t) sono indicati i due segnali idrofonici provenienti dalla base acustica già definita in
figura 1.
Tra i due segnali ed il correlatore digitale è interposto il blocco di sfasamento per 90°, sfasamento di 90° per qualsiasi frequenza della banda.
Con questa configurazione all'uscita del correlatore digitale non si ha più la C(r) ma la sua trasformata : HC(r)
L'algoritmo matematico che definisce la HC(r) è simile alla 1) ma dove compare la funzione cos(x) si trova invece la funzione sen(x) così come riportato nella 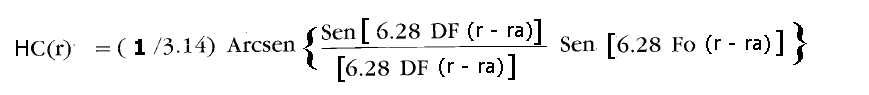2)

2)

dove:
Fo = ( F1 + F2 ) / 2
DF = (F2 - F1 ) / 2
F1 = frequenza inferiore della banda di ricezione; in Hz
F2 = frequenza superiore della banda di ricezione; in Hz
r = variabile indipendente; in Sec.
ra = d Sen( a° ) / 1530 ; ritardo dell'onda dovuto alla posizione angolare del bersaglio.
a° = angolo di puntamento del bersaglio; in gradi
d = lunghezza della base; in m.

La dimostrazione della 2), molto complicata, ci porterebbe fuori dall'argomento della pagina, ci limiteremo ad esaminarne l'andamento con i dati numerici utilizzati nel paragrafo 2.
L'andamento di HC(r), per F1 = 2000 Hz e F2 = 10000 Hz, ed a = 27°, è riportato in figura 4 per r variabile da 0 a 1000 μ Sec.



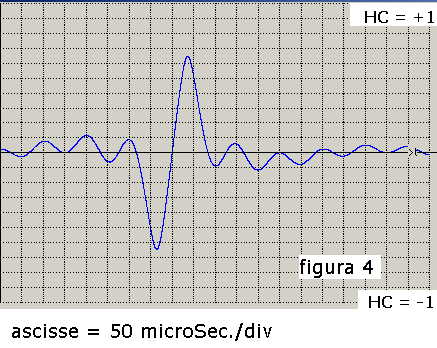
La curva mostra come al posto del massimo di C(r), per r = 400 μSec. la HC(r) ha uno zero oltre il quale è positiva o negativa in base alle variazioni di ra.
Supponiamo ora che con il sonar, che impiega la 2), si sia puntato il bersaglio fermo su a = 27°, ciò è reso possibile dopo aver variato r per ottenere r = ra.
Se dopo il puntamento della sorgente questa si sposta angolarmente verso destra, ad esempio
per a = 27.5°, cresce il valore di ra e l'argomento di sen[ 6.28 Fo ( r - ra ) ] della 2) trovandosi con r < ra renderà la funzione negativa indicando lo spostamento del bersaglio verso destra.
Se invece dopo il puntamento per a = 27° del bersaglio fermo, sempre dopo aver variato r per
ottenere r = ra, la sorgente si sposta angolarmente verso sinistra, ad esempio per a = 26.5°, decresce il valore di ra e l'argomento di sen[ 6.28 Fo ( r - ra ) ] della 2) trovandosi con r > ra renderà la funzione positiva indicando lo spostamento del bersaglio verso sinistra.

4) Osservazioni
La funzione HC(r) è impiegata sia per i sistemi RLI, sia per gli anelli, hardware o software, relativi ai sistemi automatici per l'inseguimento dei bersagli; una o più sorgenti acustiche in movimento possono essere inseguite contemporaneamente utilizzando la 2) a tutto vantaggio delle prestazioni operative del sonar.
Sempre la HC(r) può essere utilizzata per l'intercettazione delle emissioni sonar con i sistemi detti
BDI ( Bearing Deviation Indicator ) .
La HC(r) è subordinata alle caratteristiche di guadagno sul rapporto Si/Ni così come i processi di correlazione normale trattati in altre pagine di questo sito; per tale ragione le costanti di tempo d'integrazione nei correlatori che elaborano la HC(r) dovranno essere diverse in dipendenza del tipo d'impiego:
-costanti di tempo elevate per i sistemi RLI destinati all'elaborazione dei segnali di rumore emessi dai bersagli; quindi notevoli guadagni sul rapporto Si/Ni.
-costanti di tempo brevi per i sistemi BDI destinati ad operare su segnali impulsivi delle emissioni sonar intercettate o su gli echi delle emissioni proprie; quindi guadagni modesti sul rapporto Si/Ni.