1) Generalità
Sulle modalità di misura della forza del bersaglio, il TS (Target Strength), e su alcuni valori ad essa conseguente, rilevati sul campo, si e già ampiamente trattato alla pagina p8; nella presente valuteremo, da un punto di vista prevalentemente geometrico, la variazione del TS in funzione delle tre principali variabili dalle quali dipende:
-Angolo di vista
-Frequenza dell'impulso
-Durata dell'impulso
Le nostre considerazioni partiranno sempre dall'espressione classica che definisce il TS, in dB, come rapporto tra l'energia riflessa Ir e l'energia incidente Ii secondo la :
TS(dB) = 10 Log ( Ir / Ii ) .

2) Dipendenza del TS dall'angolo di vista
La forma spaziale dei possibili bersagli può essere assimilata, con sufficiente approssimazione, alla combinazione geometrica di forme elementari, ognuna delle quali contribuisce per riflessione speculare alla determinazione del TS del corpo nel suo insieme.
Nelle strutture reali esistono però centri o zone di reirradiazione diffusa, i cui contributi vanno a sommarsi a quelli originati dalle riflessioni speculari; in funzione della composizione geometrica del corpo e della conformazione e della localizzazione delle zone diffondenti, le ampiezze e le fasi di ciascuna di queste componenti varieranno al variare dell'angolo di vista del bersaglio, determinando una variazione angolare del valore TS.
Nella figura 1 è riportato il diagramma polare dell'andamento del TS di un sommergibile d'alto mare il cui valore varia, come già accennato, in funzione dell'angolo di vista.



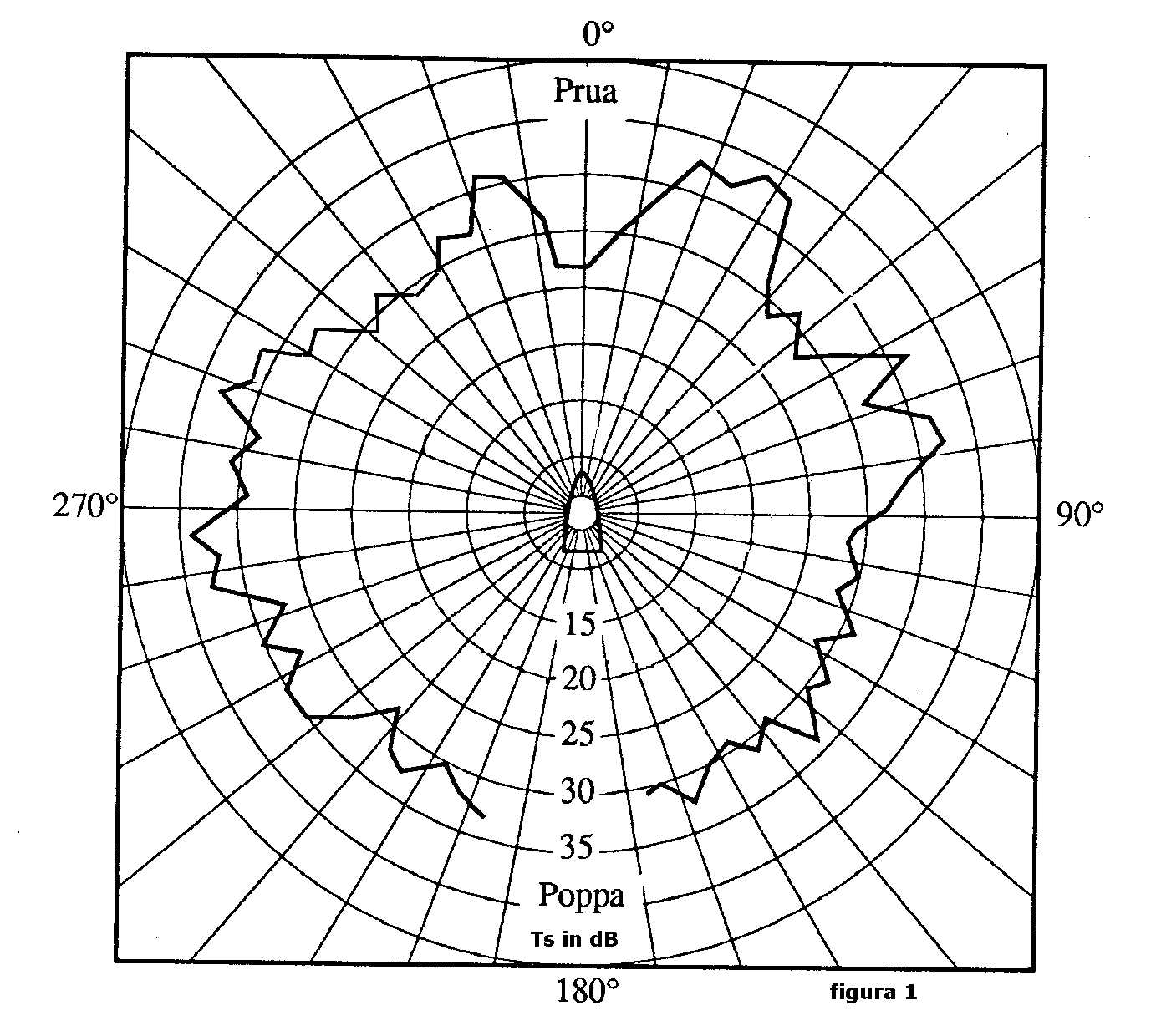
La curve è state determinate alla frequenza di 24 KHz con una risoluzione angolare di 5°.
Il diagramma mostra il classico profilo a farfalla con il massimo dispiegamento delle ali nell'intorno del traverso del bersaglio, dove gli angoli di vista abbracciano la superficie più elevata del sommergibile, mentre il TS si riduce a prua e a poppa per angoli di vista di 0° e 180°.
Il massimo valore del TS nell'intorno del traverso è dell'ordine di 35 dB, a prua di circa 25 dB.
A titolo informativo si fà presente che la simulazione di un bersaglio simile al sommergibile menzionato per eseguire misure in mare, tale da presentare un TS = 35 dB per qualsiasi angolo di vista, è praticamente impossibile: la dimensione ( diametro d ) che tale bersaglio sferico dovrebbe avere per presentare un
TS = 35 dB è:

d = 2 √ [ 10 ^ (Ts/10) ] = 112 metri ! ! !

3) Dipendenza del TS dalla frequenza dell'impulso
Nell'ipotesi di grande distanza tra sorgente e bersaglio e nel caso che la lunghezza d'onda del segnale, contenuto nell'impulso, sia molto più piccola delle dimensioni del bersaglio il valore del TS diventa dipendente dalla frequenza secondo alcune espressioni legate alla geometria del bersaglio.
Uno dei casi più semplici vede il bersaglio come un cilindro di raggio "r" e lunghezza "L" per il quale il legame tra TS e frequenza è espresso da:

TS = 10 Log ( r L^2 / 2 λ )

dove λ ( lunghezza d'onda ) = c / f
c = 1530 (velocità del suono in acqua)

L'applicazione della formula per un cilindro dalle dimensioni:
r = 50 m; L = 100 m ( dimensioni di comodo per evidenziare il fenomeno )
per f variabile da 100 Hz (pari a λ = 15m) a 20000 Hz (pari a λ = 7.6 cm)
porta al diagramma di figura 2 che vede il Ts variare da 42 dB a 65 dB quando la frequenza varia da 100 a 20000 Hz



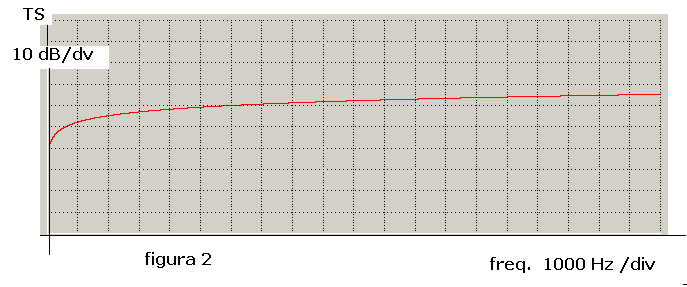
Il comportamento indicato in figura 2 è spiegabile in modo semplice; le areole del cilindro eccitate dall'impulso, grazie all'incrementarsi del rapporto L / λ dovuto al crescere della frequenza f, si comportano come singoli emettitori di un sistema direttivo sommando al fenomeno della riflessione normale anche un certo guadagno di direttività che incrementa il TS.

4) Dipendenza del TS dalla durata dell'impulso
La durata dell'impulso subordina il livello del TS in modo proporzionale alla durata stessa secondo la geometria di figura 3 che andiamo a commentare:



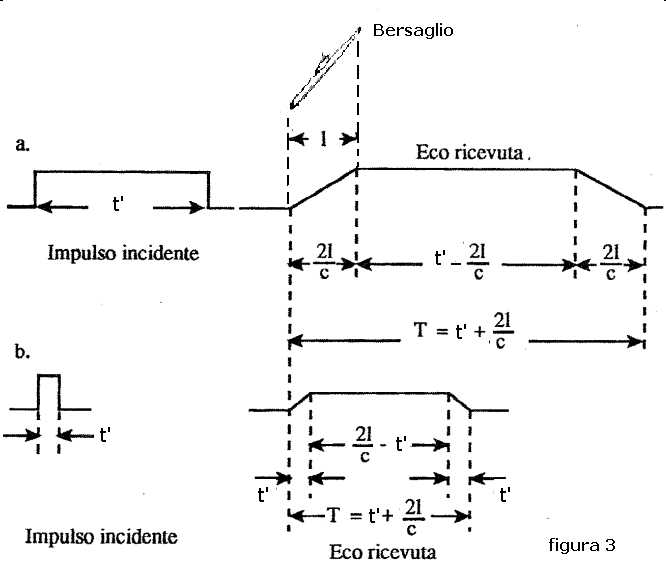
Nella parte superiore del disegno è tracciata la siluette di un sommergibile che viene assunto come bersaglio per la dimostrazione, detto bersaglio è ipotizzato come corpo omogeneo visto di lunghezza "l" dalla direzione di propagazione dell'impulso che lo colpisce.
Indicata con "R" la distanza tra emettitore e bersaglio e con t' la durata dell'impulso emesso, la sua lunghezza "lng" è: lng = c t'( dove "c" è la velocità del suono in acqua ).
Il fronte iniziale dell'impulso colpisce la prua del bersaglio dopo un tempo R/c rispetto al momento d'emissione e ritorna alla sorgente dopo un tempo T1 = 2 R/c.
Il fronte finale dell'impulso colpisce la prua del bersaglio al tempo t' + R/c e la poppa al tempo t' + R/c + l/c ritornando alla sorgente dopo un tempo T2 = t' + 2R/c + 2l/c .
La durata Te dell'eco ricevuta dalla sorgente è pertanto:
Te = T2 - T1 = (t' + 2R/c + 2l/c)- 2 R/c = t1 + 2l/c .
Il valore di Te mostra come la durata dell'impulso riflesso sia più estesa dell'impulso incidente per la differenza pari a 2l/c .
Quando la durata dell'impulso t' è superiore al tempo necessario per l'illuminazione totale del bersaglio:
t' > 2l/c
l'ampiezza dell'eco è proporzionale all'ampiezza dell'impulso incidente ma è indipendente dalla sua durata così come mostra la sezione "a" della figura 3.
Se invece la durata dell'impulso è inferiore al tempo necessario per l'illuminazione totale del bersaglio:
t' < 2l/c
l'ampiezza dell'eco, pur restando proporzionale all'ampiezza dell'impulso, decresce con il ridursi della dura t' così come si vede nella sezione b di figura 3.
Rilievi sperimentali sull'argomento sono stati condotti su sommergibili come bersagli, uno tra i molteplici risultati è riportato in figura 4 per tre diverse durate d'impulso: 1 mSec, 10 mSec, 30 mSec.



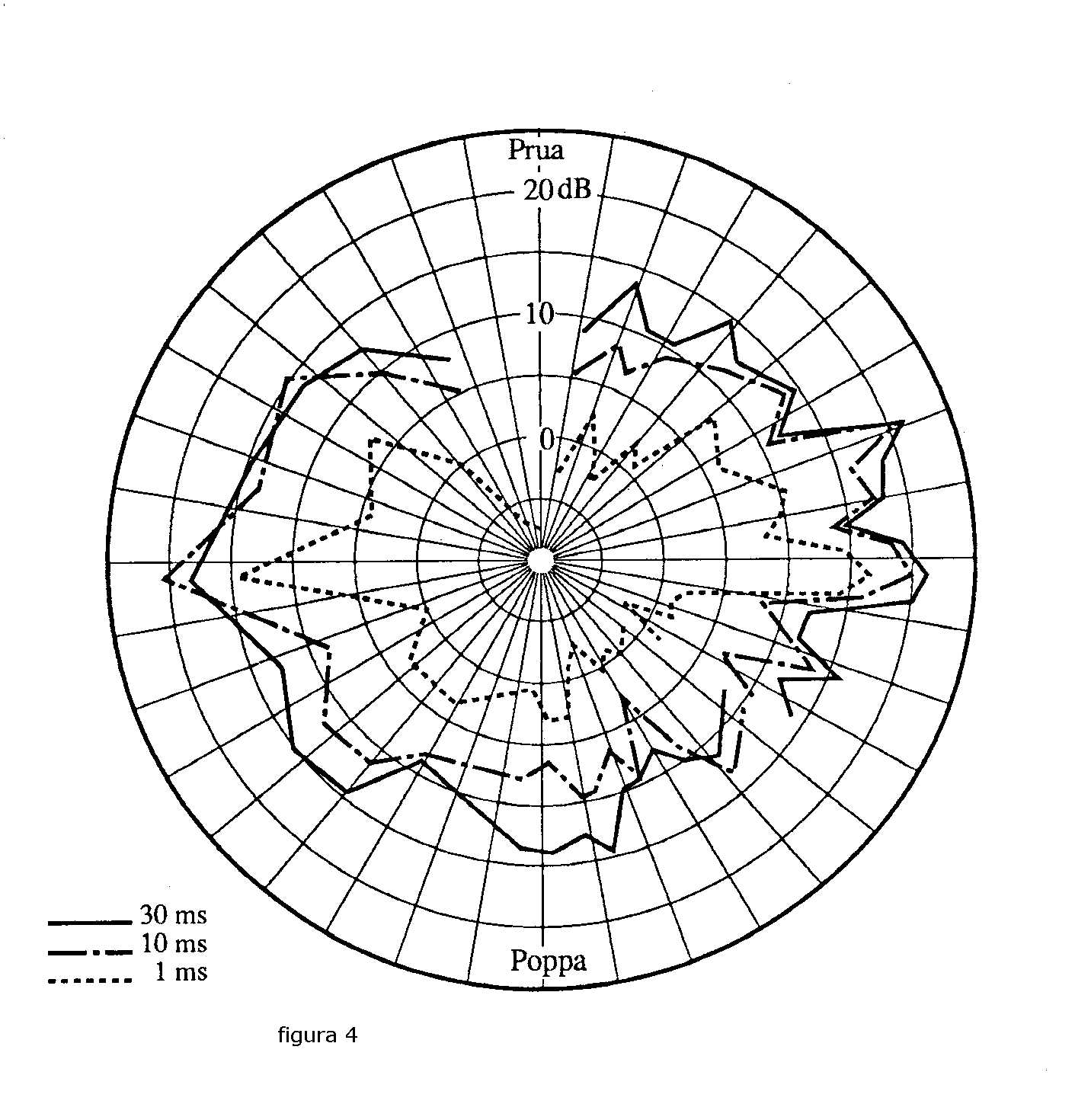
Dal diagramma, paragonando tra loro i tracciati, si evince che per t' = 1 mSec. era valida la condizione
t' < 2l/c, mentre tra t' = 10 mSec e t' = 30 mSec. era valida la condizione di t' > 2l/c.