1) Generalità
I sistemi interferometrici subacquei sono basi acustiche caratterizzate da una elevatissima "Risoluzione Angolare" (si veda p 104) che consente la scoperta della presenza contemporanea di bersagli, vicini tra loro, e molto lontani dalla base acustica di rilevamento.
Alta risoluzione s'identifica con direttività molto spinta; le basi in oggetto richiedono pertanto l'elaborazione dei segnali in correlazione e notevoli estensioni come si vedrà nel prosieguo della pagina.

2) Sulla lunghezza e la frequenza di lavoro della base
Se prendiamo in esame la funzione C(tao) = C(a°, F, d) che definisce la direttività in correlazione di una base idrofonica rettilinea calcolata per due soli idrofoni come in figura 1:



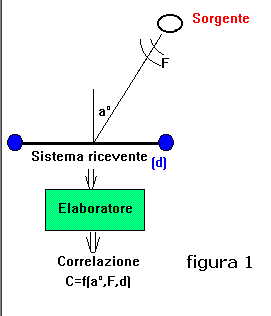
abbiamo:

1)

dove:
f = frequenza superiore della banda compresa tra 0 ed f.
tao = (d / c) Sen ( a° ) secondo la figura 1
d = lunghezza della base
c = 1530 m/Sec velocità media del suono

La C(tao) espressa dalla 1) è definita da una curva detta direttività della base in correlazione, la larghezza del lobo principale misurata a -3dB sotto il picco massimo, vedi figura 2, definisce il valore limite della "Risoluzione Angolare " Δα (l'argomento relativo al limite della "Risoluzione Angolare è sviluppato su p104).



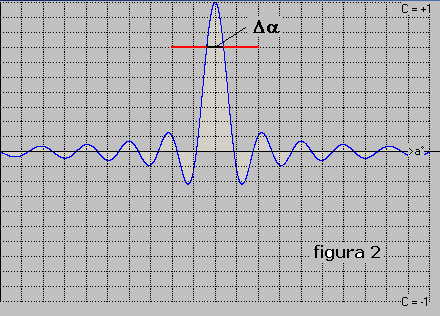
Nella 1) compare la funzione del tipo Sen x / x che caratterizza l'ampiezza a - 3 dB individuata dalla variabile Δα, si può quindi scrivere l'equazione trascendente :
Sen (x) / (x) = 0.707    2)
dove:
x = 2 (3.14159 tao f)
La soluzione della 2), o per via analitica o tabellare, porta a:
x = 1.4, quindi 2( 3.14159 tao f ) = 1.4, ma essendo:
tao = (d / c) Sen ( a° ) si ha:
3.14159 (2 d f / c ) Sen ( a° ) = 1.4    3)
Quest'ultima equazione risolta in a° come funzione della variabile "d" e della frequenza f, porta alla seguente espressione di Δα in gradi intesa sempre misurata a - 3 dB sotto al massimo:

Δα = 2 a° = [ 2 arcSen ( 682 / 2 f d )] ( 180 / 3.14 )    3)

Come si vede dalla 3) il Δα è tanto più piccolo quanto è elevato il valore "d" e/o la frequenza "f";
sarà quindi la "Risoluzione Angolare" migliore per valori elevati delle varibili "d" e/o "f".
Quando i valori di Δα sono piccoli l'arco si confonde con il seno e Δα risulta praticamente inversamente proporzionale a "d" e/o la frequenza "f".
E' utile dalla 3) esplicitare "d" o "f" in funzione di a° secondo le espressioni:

d = 680 / [f Sen ( a° )]    4)
f = 680 / [d Sen ( a° )]

3)Il diagramma della funzione a° = f( d )
Secondo la 3), una volta fissato il limite f della frequenza della banda, si può tracciare il grafico di a° = f( d ) per avere l'andamento globale della "Risoluzione Angolare" sul quale ragionare e decidere per la soluzione dei propri problemi.
In figura 3 è riportato il grafico della funzione interessata per banda di frequenza costante da 0 a f = 1000 Hz, e "d" variabile da 1 m a 100 m:



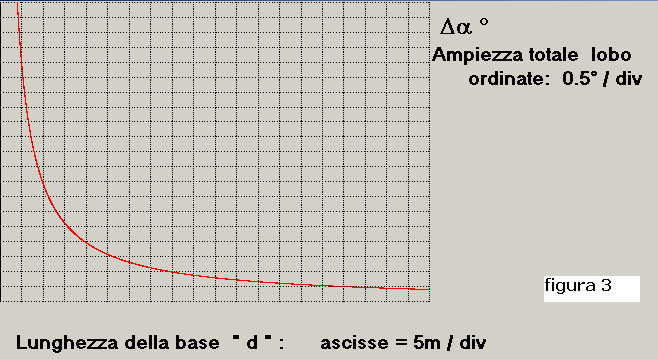
Come si vede da figura 3, data la banda 0-1000 Hz, per d = 100 m il valore del Δα è: Δα ≈ 0.5° .

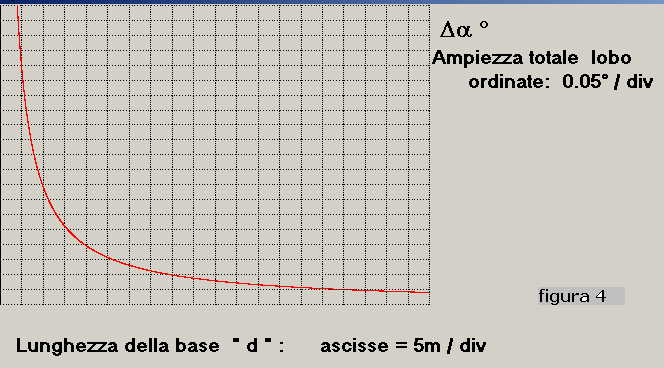
Se portiamo il limite di banda a 10000 Hz si una risposta che porta a un Δα ≈ 0.04° per d = 100 m così come si evince da figura 4:

4)Sulla discriminazione angolare
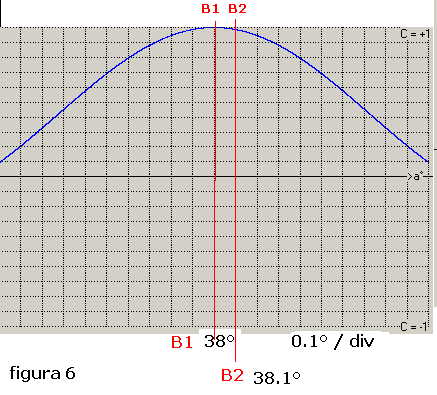
Osserviamo ora la figura 5 dove è riportata una possibile condizione operativa che vede due bersagli B1 e B2 rilevabili angolarmente dalla base interferometrica secondo gli angoli:
α1 = 38° e α2 = 38.1° con una differenza angolare x = 0.1°



Supponiamo che la base lavori in banda 0-1000 Hz e che abbia una lunghezza d = 40 m, dalla figura 3 si può stabilire che valore di Δα è circa 1°, in tali condizioni non è possibile discriminare la posizione dei due bersagli che essendo a distanza angolare di x = 0.1° interferiscono tra loro in quanto entrambi i segnali sono ricevuti all'interno del lobo di direttività della base che è ampio 1° così come mostra figura 6 tracciata secondo la 1).



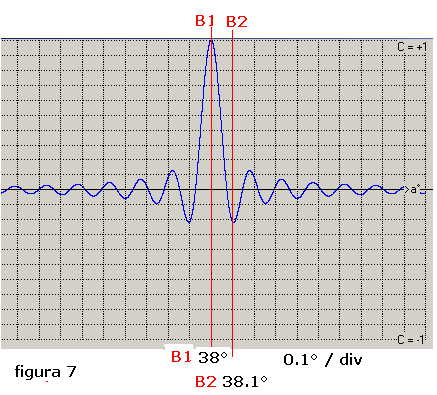
Se invece si considera, ad esempio, una base della lunghezza di 60 m che riceve in banda 0-10000 Hz il valore di Δα, rilevato da figura 4, è circa 0.06°; in questo caso la base può essere puntata verso B1 senza interferenza di B2 e successivamente su B2 senza interfeenza di B1 così come mostra la figura 7 tracciata anch'essa secondo la 1).

5)Basi interferometriche in banda f1-f2
In precedenza abbiamo esaminato il comportamento di basi interferometriche che lavorano in banda 0-f (banda definibile con filtri passa basso) deducendo gli algoritmi per il calcolo delle loro caratteristiche; cosa analoga sarebbe auspicabile per basi che lavorano nel campo f1-f2 ( definito da filtri passa banda ) le cui direttività in correlazione sono espresse dalla seguente funzione:

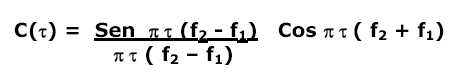5)

dove:
f1 = frequenza inferiore della banda
f2 = frequenza superiore della banda
tao = (d / c) Sen ( a° ) secondo la figura 1
d = lunghezza della base
c = 1530 m/Sec velocità media del suono

Dalla 5) non è possibile ricavare la relazione Δα = f ( d ) con metodi semplici; la soluzione del problema è fattibile, empiricamente e con qualche approssimazione, utilizzando il procedimento di calcolo precedente che prevede un solo valore di frequenza "f" opportunamente ricavato dai valori di f1 ed f2 che definiscono la 5).
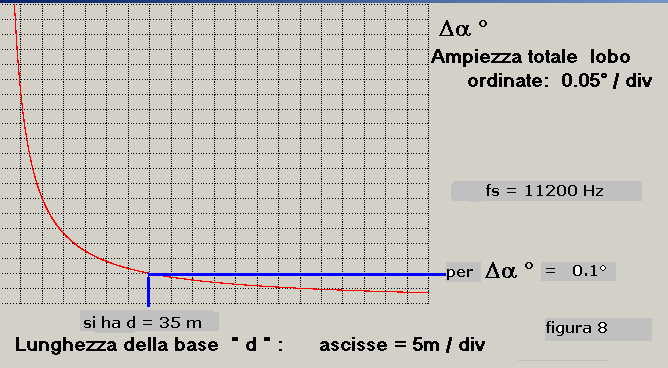
Prendiamo ad esempio il caso nel quale si debba determinare la lunghezza " d " per una base interferometrica operante nel campo di frequenza compreso tra:
f1 = 4000 Hz; f2 = 12000 Hz per ottenere un Δα = 0.1°
s'inizia calcolando il 70% della somma ( f1 + f2 ) = Fs = 11200 Hz
si applica la 3) per " d " variabile da 1 a 100 m e f = fs = 11200 Hz e si ottiene la curva di figura 8 dalla quale il valore di Δα = 0.1° si ottiene per "d " = 35 m.

6)Dimensionamento basi interferometriche con metodo iterativo
I calcoli eseguiti in precedenza possono essere sviluppati con metodo iterativo con l'ausilio dell'eseguibile esercor.exe ( si vedano esercizi d'impiego su p157 ).
Il metodo in oggetto si utilizza come segue:
1) si clicca su esercor.exe
2) nella finestra che compare si seleziona il tipo di funzione di correlazione richiesta:
se ad esempio si deve svolgere il calcolo di cui al paragrafo 5) si seleziona la funzione e si inseriscono i due valori che definiscono la banda e s'impostano le scale del reticolo come mostra la figura 9:



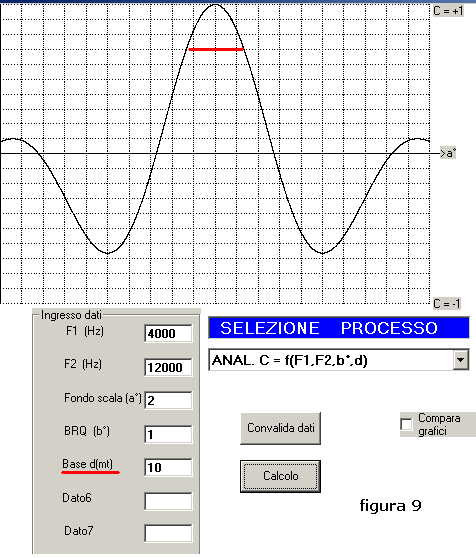
3) si introduce un primo valore del " d " cercato (ad esempio "d" = 10 m)
4) dopo la "convalida dati" il pulsante "calcolo" si ha la comparsa del grafico della funzione
5) si valuta l'ampiezza della curva al livello 0.07 (- 3 db) -tratto rosso di figura 9-, in essa il valore di Δα è di circa 0.24°; molto lontano dal Δα = 0.1° voluto
6) si ripete il calcolo con valori mano a mano crescenti di "d" fino al raggiungimento di un valore di Δα il più vicino possibile a quello cercato; risulterà risolto il problema con la coppia "d" = 33 m e Δα = 0.1° con una differenza in "d" del 6% rispetto alla soluzione ottenuta nel paragrafo 5)

Scegliendo la funzione di correlazione adatta si può risolvere per via iterativa anche il problema impostato per le bande 0-f.