SONAR-INFO-p167
Considerazioni sulla misura della distanza in emergenza 1) Generalità 2) Sulla funzione Si/Ni = f [ C(o) ] 3) L'equazione del sonar 4)Il legame tra Si/Ni, il DT e la banda BW 5)L'equazione generale per il calcolo della "distanza" 6)La fragilità nella misura della "distanza" 7)Algoritmo per distanze brevi 8)Osservazioni sulle distanze brevi (Caso di C(o) molto elevato) 9)Note su alcune variabili di calcolo
Il sonar d'emergenza FALCON, trattato estesamente nella sezione di ricerca veloce ad esso dedicata,
è stato ideato a seguito dell'esigenza illustrata nella diapositiva che sotto riportiamo:


Quando un sommergibile si trova a quota profonda ed ha il sonar operativo in avaria
l'unica soluzione per la risalita in sicurezza consiste in un sonar d'emergenza assolutamente
indipendente dall'elettronica dell'apparato principale.
Il sonar d'emergenza fornisce al comando le direzioni di provenienza dei diversi semoventi
del teatro operativo; non ha alcuna caratteristica acustica in grado di stabilirne la distanza.
Un metodo, estremamente grezzo, per avere un'idea della "distanza" del semovente interessato
consiste nella misura del rapporto Segnale/Disturbo d'ingresso del sonar, (Si/Ni), al momento del rilevamento della sorgente
acustica.
La misura che si esegue, pur affetta da errori molto elevati, è l'unica informazione ottenibile
in condizioni di estrema incertezza nella riemersione del battello: meglio una misura incerta
che nessuna misura .
Illustriamo di seguito gli algoritmi dai quali ricavare quello generale per il computo
della "distanza" alla quale abbiamo fatto riferimento.
In p165 possiamo vedere quali legami teorici sussistano tra il rapporto Si/Ni e il livello di
correlazione esistente tra due segnali applicati ad un correlatore a coincidenza di polarità
facente parte del sistema di scoperta di un sonar.
La relazione esistente è riportata nella 1) dove C(o) è l'ampiezza normalizzata della funzione
di correlazione facilmente rilevabile in un dispositivo di rivelazione a coincidenza di polarità:
 1)
1)
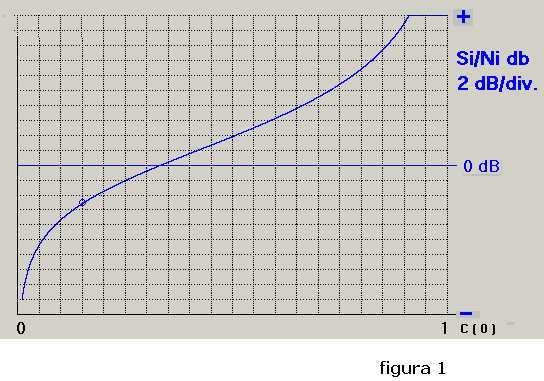
L'andamento della 1) in funzione di C(o) è riportato in figura 1; in ascisse il valore di C(o)
normalizzato, da 0 ad 1, in ordinate il valore di Si/Ni espresso in dB (+/- 20 dB).
La presenza di un cerchietto sulla curva sarà spiegata in seguito.
La 1) gioca un ruolo fondamentale nella costruzione dell'algoritmo che consente il calcolo
della "distanza" di una sorgente acustica.
Altri due algoritmi necessari al calcolo della "distanza" sono costituiti dalle due equazioni per
la determinazione della portata di un sonar così come mostra la 2)

Le variabili che compaiono nella 2) sono ora elencate dividendole in due gruppi:
Gruppo caratteristico del sonar ( dati di fabbrica o predisposizioni funzionali )
DI = guadagno della base ricevente -in dB-
DT = soglia di rivelazione -in dB-
BW = banda di ricezione -in Hz-
GN = guadagno canale audio al rumore del mare
RC = cost. d'integrazione -in Sec.-
Gruppo caratteristico dell'ambiente operativo
SL = livello di emissione acustica del semovente -in dB/μPa/Hz/1m-
NL = livello del rumore del mare -in dB/μPa/Hz
R = distanza del semovente -in Km-
a = coeff. d'assorbimento del mezzo -in dB/Km-
Si/Ni = rapporto segnale/disturbo d'ingresso -in dB-
h = modello di propagazione sferica
La quarta ed ultima equazione necessaria alla soluzione teorica del problema posto è
sotto indicata:
Si/Ni = DT - 10 Log BW 3)
dove Si/Ni in dB indica il rapporto segnale disturbo all'ingresso del sistema di correlazione.
L'equazione generale è data dalle interrelazioni dell'insieme delle quattro esaminate in precedenza:
 1)
1)

Si/Ni = DT - 10 Log BW 3)
Elaborandole ad arte si ottiene la funzione definitiva R = f[ C(o) ] che lega la distanza di
acquisizione ( "distanza" R al momento della misura ) al valore del livello di C(o) misurato
all'uscita del correlatore allo steso momento.
La R = f[ C(o) ] è un'equazione trascendente risolvibile soltanto con un processo di calcolo
iterativo da implementare in un P.C.
Il programma citato può essere implementato
nella routine generale che realizza il sonar d'emergenza.
Una presentazione della R = f[ C(o) ], calcolata con una routine in VB, con la serie di dati
sotto indicati è mostrata in figura 2.
Dati di fabbrica e dati d'ambiente impostati per il calcolo dimostrativo su di un sonar di emergenza:
SL = nave a 20 nodi
NL = mare a forza 2
BW = 1500-3000 Hz
a = 0.13 dB/Km
DI = 10 dB
DT = 27 dB ( per d = 28; Priv = 99% Pfa = 0.1 % )
RC = 0.1 Sec.
h = propagazione sferica
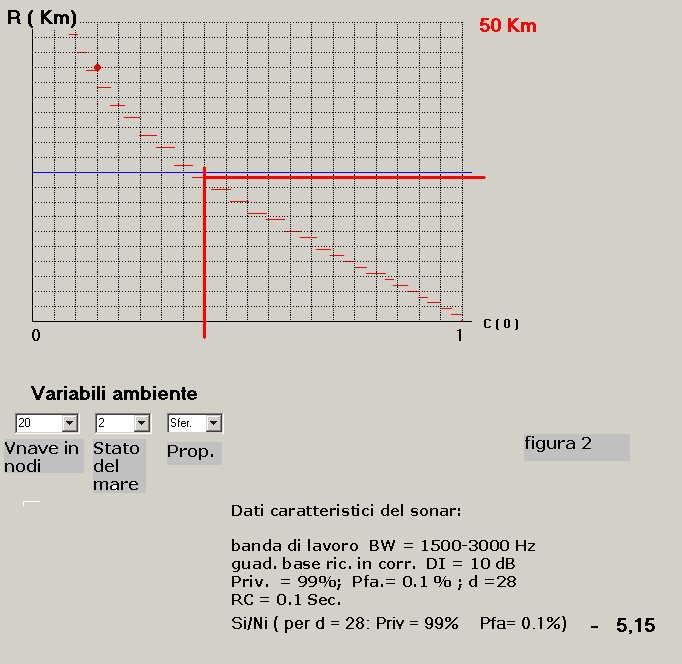
In figura l'andamento della R = f[ C(o) ] è tracciato con piccoli segmenti rossi; per C(o)
variabile da 0 a 1 la R si estende da R = 48 Km circa ad R = 1 Km circa.
Il punto rosso all'altezza di 42 Km circa, ottenuto per C(o) = 0.15, indica la portata massima del sonar nelle
condizioni imposte: ( DT = 27 dB ).
Se ad esempio l'operatore, a seguito di un avvicinamento della nave per SL ed NL come da impostazione ,
misurasse un valore
di C(o)= 0.4 potrebbe stabilire sulla curva di figura 2, in via teorica e con ragionevole approssimazione, la distanza
reale alla quale si trova la sorgente acustica, pari quindi a circa Rsorg. = 24 Km.
Essendo la portata massima calcolata R = 42 Km, valida per DT = 27 dB
( per d = 28; Priv = 99% Pfa = 0.1 % ) si pò asserire che tali parametri sono a maggiore
ragione validi per Rsorg. = 24 Km.
A chiusura del paragrafo osserviamo che il metodo di calcolo illustrato, non essendo a carattere
geometrico, segue un processo subordinato alle tolleranze delle variabili
acustiche in gioco che, anche nelle migliori condizioni di rilevamento, sono di difficile
valutazione.
Il valore di Rsorg. = 24 Km ottenuto nel paragrafo precedente parte dall'assunto che
due variabili ambiente SL (corrispondente ad una nave a 20 nodi) ed NL (corrispondente ad uno
stato del mare pari a SS = 2 ) siano state impostate con la certezza assoluta che tali
valori corrispondano alla reale situazione del teatro logistico.
Questa situazione non risponde a realtà una volta che il sistema di
misura venisse attivato con il sommergibile in profondità e senza sonar operativo.
A questo punto è compito dell'operatore esperto valutare come segue, mediante l'ascolto
idrofonico, le due variabili citate:
a)Disposto il puntamento d'ascolto del sonar d'emergenza in direzione libera da
sorgenti acustiche l'operatore deve valutare tramite il canale audio, a mezzo del valore
noto di GN, il corrispondente stato del mare.
b) Disposto il puntamento d'emergenza sulla sorgente acustica dovrebbe valutare, in base al
timbro del rumore e alla velocità di rotazione delle eliche, la presunta velocità del semovente
per inserirla, assieme allo stato del mare valutato in a), nel programma di calcolo facente
parte delle routine di governo del sonar d'emergenza.
Supponiamo ora che le condizioni reali sul campo siano quelle dell'esempio al paragrafo 5);
l'operatore, secondo la procedura a) può valutare il rumore del mare vicino a quello reale
di( SS = 2 ).
Nella determinazione del rumore del semovente la cosa diventa difficile quindi la valutazione
della velocità è lasciata alle capacità sensoriali dell'operatore; supponiamo che esso ritenga
che la velocità sia intorno a 15 nodi ( velocità inferiore a quella reale ); inserirà quindi a
calcolo SS = 2 e Vn = 15 ottenendo
un grafico sostitutivo del precedente di figura 2 secondo la figura 3:
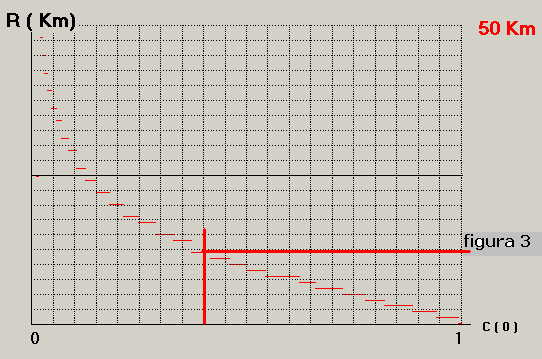
Dato che le condizioni ambientali reali sono state ipotizzate ancora come per l'esempio di
figura 2 la misura del valore di C(o) sarà ancora la stessa quindi l'operatore leggerà
C(o) = 0.4 deducendo, secondo la curva di figura 3, un valore di Rsorg = circa 12.5 Km .
Il valore misurato Rsorg = 12.5 Km è la metà di quello reale, ma sufficiente quindi a garantire
ancora una riemersione del sommergibile.
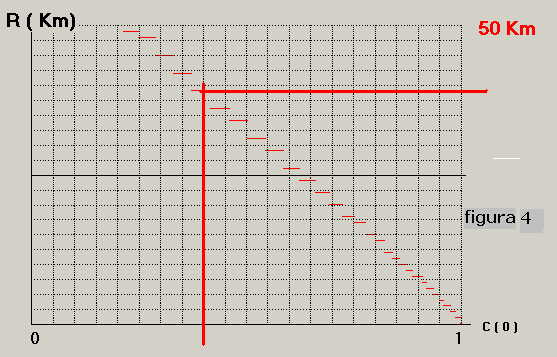
Se l'operatore, nella valutazione della velocità della sorgente, la considera superiore a quella
reale, ad esempio Vn = 25 nodi, si ha la curva di figura 4 che, sempre per C(o) = 0.4, rileva un
valore di Rsorg. = circa 38 Km.
Le misure eseguite, nella loro estrema fragilità, suggeriscono di eseguire una valutazione
della velocità del semovente inferiore a quella stimata in modo tale che la Rsorg.
misurata tende ad essere minore della reale fornendo
al comando un dato di "distanza" che pur estremamente indicativo può garantire più sicurezza
nella delicata fase di riemersione.
E' chiaro che una procedura così sensibile dovrebbe essere sperimentata a lungo su di un
sonar d'emergenza prototipico prima di validarla in modo generale.
Un algoritmo da impiegare per la misura della "distanza" su brevi tratti di mare è stato studiato;
si tratta di una funzione esponenziale, che pur se complessa, non necessita di routine
iterative ma può essere messa a calcolo come una funzione normale.
Il nuovo algoritmo scaturisce sempre dal gruppo delle quattro funzioni di paragrafo 3, con
la 2) privata del termine "aR" che, date le caratteristiche di BW del sonar d'emergenza, diventa
trascurabile per brevi distanze.
L'espressione della nuova R = f[ C(o) ] è riportata nella 4):
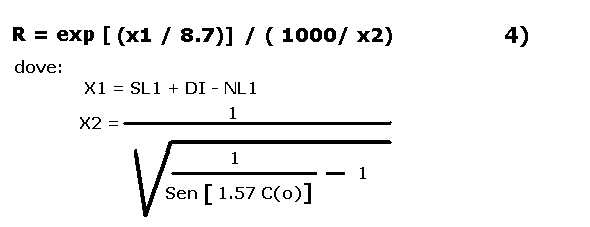
Il grafico della 4) è riportato in figura 5 per C(o) variabile da 0.15 ad 1 e R da 0 a 5000 m:
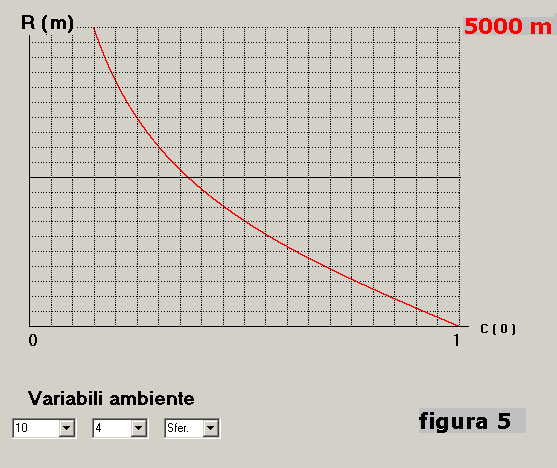
Con la 4) è possibile calcolare immediatamente la "distanza" funzione di C(o) con una normale
routine su P.C. senza l'esigenza del tracciamento della curva.
Se il valore di C(o) è molto elevato, supponiamo ad esempio C(o) = 0.8, significa che il rapporto
SI/Ni è anch'esso elevato; questa situazione può dipendere da due cause diverse tra loro:
1) Il rumore del mare è molto basso (condizione facilmente rilevabile secondo il punto a) di
paragrafo 6).
Se il rumore del mare è molto basso il computo della "distanza" può essere eseguito come
nei casi citati in paragrafo 6.
2) Il semovente è molto vicino al sommergibile (la situazione richiede estrema attenzione).
Se la condizione 1) non è verificata significa che in realtà la nave è vicina al sommergibile;
supponiamo ad esempio che le condizioni nel teatro operativo siano con certezza assoluta:
Nave a 10 nodi
Distanza della nave R = 750 m
Stato del mare SS = 4
In tal caso, mediante la 4), possiamo calcolare la curva R = f[ C(o)] così come risulta da figura 6:
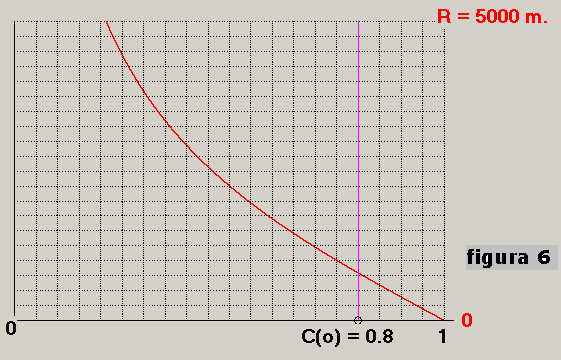
mettendo in evidenza che il valore di C(o) per R = 750 m è: C(o)= 0.8.
Il valore di C(o) rilevato dalla figura sarebbe identico a quello misurato sul sonar d'emergenza
qualora fossero valide le condizioni imposte per l'esempio.
Se la misura della "distanza" in tali condizioni fosse fatta da un operatore che, ascoltando il
rumore emesso dalla nave sottovalutasse la sua velocità in 5 nodi potrebbe calcolare una curva
diversa dalla precedente così come risulta da figura 7 dove a tratto nero la nuova curva per 5 nodi.
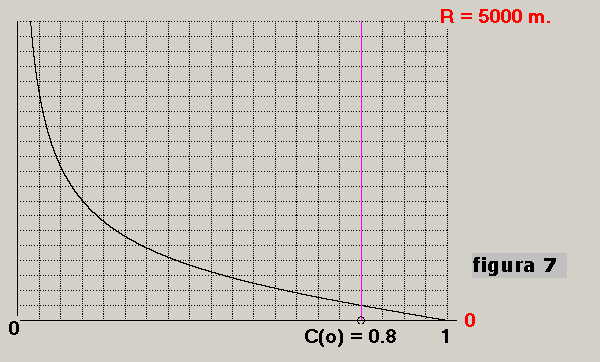
Dato che la condizione reale porta ad un valore di C(o)= 0.8 in corrispondenza di tale valore
l'operatore potrebbe valutare la "distanza" in 250 m in vece dei 750 m reali.
Se l'operatore invece sopravalutasse la velocità a 15 nodi potrebbe ottenere la curva blu di
figura 8 dove per C(o) = 0.8 dedurrebbe una distanza di 2250 m. contro i 750 reali.
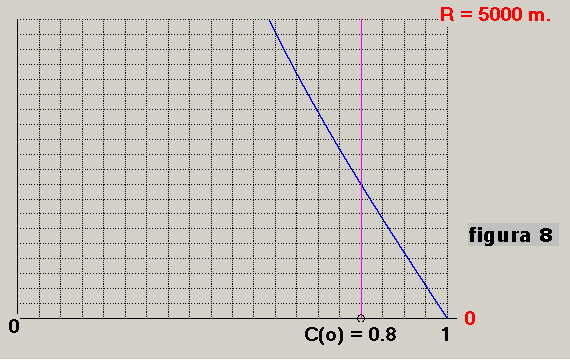
Dall'esame si evince che, in fase di valutazione della velocità della nave, è più prudente
una valutazione per difetto che non per eccesso.
Come si è visto anche in condizioni di brevi distanze la misura della "distanza" è fragile, ma è la sola
fattibile con mezzi d'emergenza.
La funzione indicata con il numero 1), rappresentata graficamente in figura 1, mostra come
varia il rapporto Si/Ni al variare di C(o).
Se ora calcoliamo Si/Ni secondo la 3) abbiamo:
Si/Ni = DT - 10 Log BW
nella quale DT = 27 dB; BW = 10 Log (3000-1500)
ne segue Si/Ni = 27 - 31.8 = - 4.8 dB
Questo valore di Si/Ni è il minimo che consente la rivelazione del segnale secondo i parametri:
Priv = 99 % ; Pfa = 0.1 % ; d = 28 assegnati al sonar di emergenza preso a modello.
Se ora poniamo un cerchietto sulla curva di figura 1 con ordinata pari a SI/Ni = -4.8 dB possiamo
dedurne l'ascissa pari a C(o) = 0.15 ; in questo modo siamo in grado di conoscere a priori che
livello normalizzato si misura all'uscita del correlatore quando Si/Ni è il limite inferiore
perché si possano verificare le condizioni di rivelazione volute.
Da quanto sopra si deduce, per il sonar di emergenza ipotizzato, che per valori di C(o) > 0.15
sono sempre verificate le condizioni ottimali di rivelazione della sorgente acustica con le
variabili esposte nel paragrafo 5 , per valori
di C(o) < 0.15 vengono, progressivamente, a mancare tali condizioni.