SONAR-INFO-p169
Calcolatore integrali definiti su archi di curve note
Calcolo del valore numerico tra i limiti d'integrazione a1 ; b1
Il calcolo del valore numerico degli integrali definiti non sempre si presta ad essere affrontato in modo semplice; in alcuni testi di matematica applicata sono disponibili numerose tabelle con le quali è possibile ricavare il valore degli integrali definiti in particolari campi di variabilità degli estremi d'integrazione.
Nelle computazioni relative alle tematiche sonar, riportate nel presente sito, sono state utilizzate, sia le tabelle, sia particolari algoritmi di calcolo appositamente studiati per le necessità contingenti; nell'intento di far cosa utile al lettore di questa pagina sono proposte, tramite un particolare file.exe ( DEFINTEGRAL) le più ricorrenti funzioni che consentono il calcolo rapido del valore numerico dell'integrale definito prescelto dall'operatore.
2) Le funzioni disponibili per l'integrazione
La raccolta delle funzioni disponibili nel file eseguibile è esposta qui di seguito senza alcun ordine, ne di complessità, ne di importanza, indicandone il nome ed esplicitandone la formula:
1) funzione parabolica :
2) funzione iperbolica ( ramo d'iperbole ):
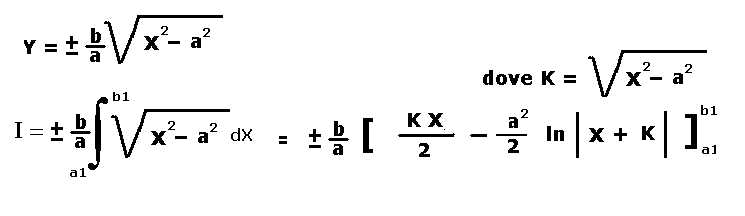
3) funzione logaritmica:
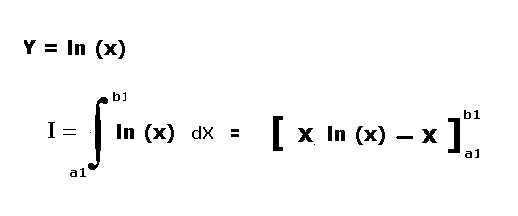
4) funzione esponenziale:
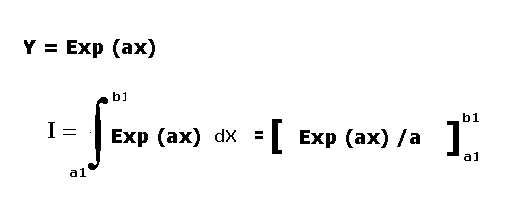
5) funzione seno :
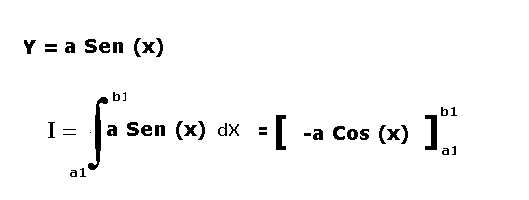
6) funzione seno x / x :
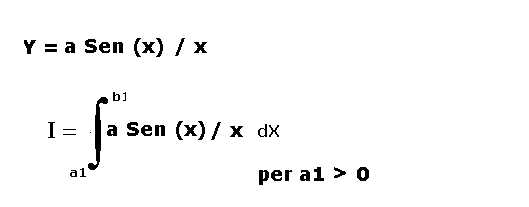
7) funzione gaussiana
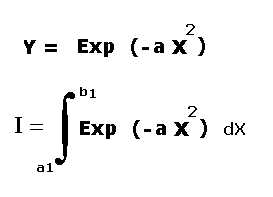
8) funzione polinomiale di Chebychev
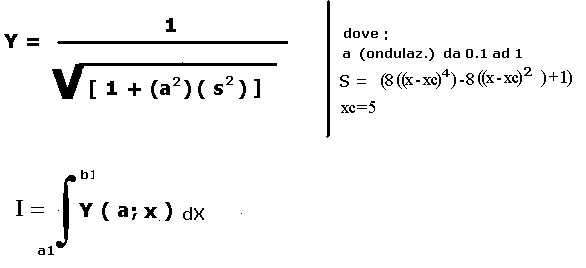
Per ciascuna delle 8 funzioni è disponibile, tramite la pagina di selezione di "DEFINTEGRAL" mostrata in figura 1, la sezione applicativa con la schermata di lavoro:
figura 1 3)L'applicativo per la funzione parabolica
Una volta selezionata, tramite l'apposito pulsante in figura 1, la funzione parabolica se ne devono stabilire le variabili richieste dalla routine nelle apposite finestre di figura 2 :
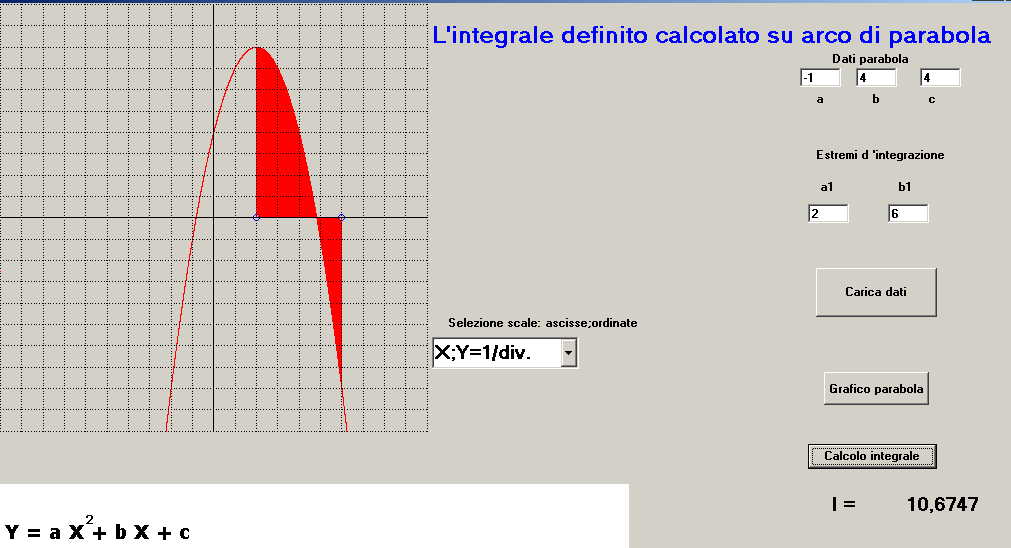figura 2 -s'impostano i coefficienti a; b; c; (supponiamo a = -1; b= 4; c = 4 )
-s'impostano i valori di scala del reticolo (ad esempio x; y = 1/div )
-s'impostano gli estremi d'integrazione a1; b1 ( nell'esempio a1 = 2; b1 = 6 )
-si clicca sul pulsante "Carica dati"
-si clicca sul pulsante "Grafica parabola" e si ha il tracciato della sola parabola,
se questo non è commisurato con le impostazioni del reticolo si ripete l'operazione con l'impostazione più adatta.
-si clicca sul pulsante "Calcolo integrale" e si ha il tracciato della parabola
e l'arco della curva definito da a1 e b1 evidenziato con area in rosso, in contemporanea, sotto il pulsante di calcolo integrale compare il valore di I = 10.6747. (si ricorda che il valore di I calcolato è la sommatoria algebrica i due superfici, una sopra l'altra sotto l'asse x, che sono di segno opposto; se si desidera il valore assoluto della superficie evidenziata si deve ripetere l'integrazione, distintamente per i due settori, sommando quindi i due valori di I ottenuti ).
La routine di calcolo per la funzione parabolica è facilmente adattabile al calcolo dell'integrale definito sud un segmento di retta; infatti se nei coefficienti della parabola, a; b; c,
si pone a = 0 si ha la presentazione di una retta dall'equazione:
Y = m x + n dove m = b ed n = c; equazione che può essere a sua volta integrata in un qualsiasi intervallo a1; b1.
4)L'applicativo per la funzione iperbolica (ramo d'iperbole)
Una volta selezionata, tramite l'apposito pulsante in figura 1, la funzione iperbolica se ne devono stabilire le variabili richieste dalla routine nelle apposite finestre di figura 3 :
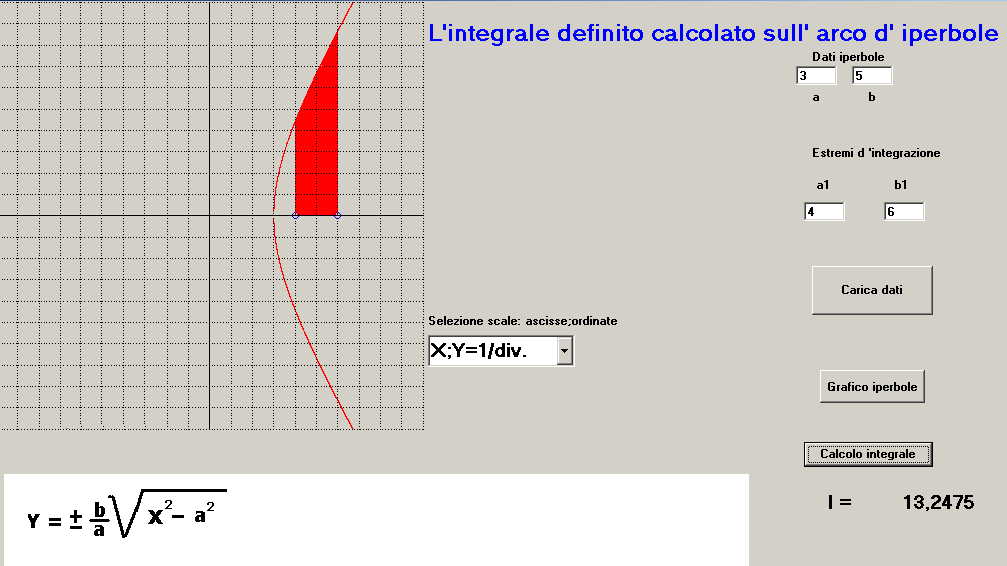figura 3 -s'impostano i coefficienti a; b; (supponiamo a = 3; b = 5)
-s'impostano i valori di scala del reticolo (ad esempio x; y = 1/div )
-s'impostano gli estremi d'integrazione a1; b1 ( nell'esempio a1 = 4; b1 = 6 )
-si clicca sul pulsante "Carica dati"
-si clicca sul pulsante "Grafica iperbole" e si ha il tracciato del solo ramo d'iperbole, se questo non è commisurato con le impostazioni del reticolo si ripete l'operazione con l'impostazione più adatta.
-si clicca sul pulsante "Calcolo integrale" e si ha il tracciato del ramo d'iperbole e l'arco della curva definito da a1 e b1 evidenziato con area in rosso, in contemporanea, sotto il pulsante di calcolo integrale compare il valore di I = 13.2475 (si osserva che in questo caso, diversamente da quanto mostrato nel paragrafo precedente, il valore di I coincide con la superficie sottesa all'arco d'iperbole.)
5)L'applicativo per la funzione logaritmica neperiana
Una volta selezionata, tramite l'apposito pulsante in figura 1, la funzione logaritmica se ne devono stabilire le variabili richieste dalla routine nelle apposite finestre di figura 4 :
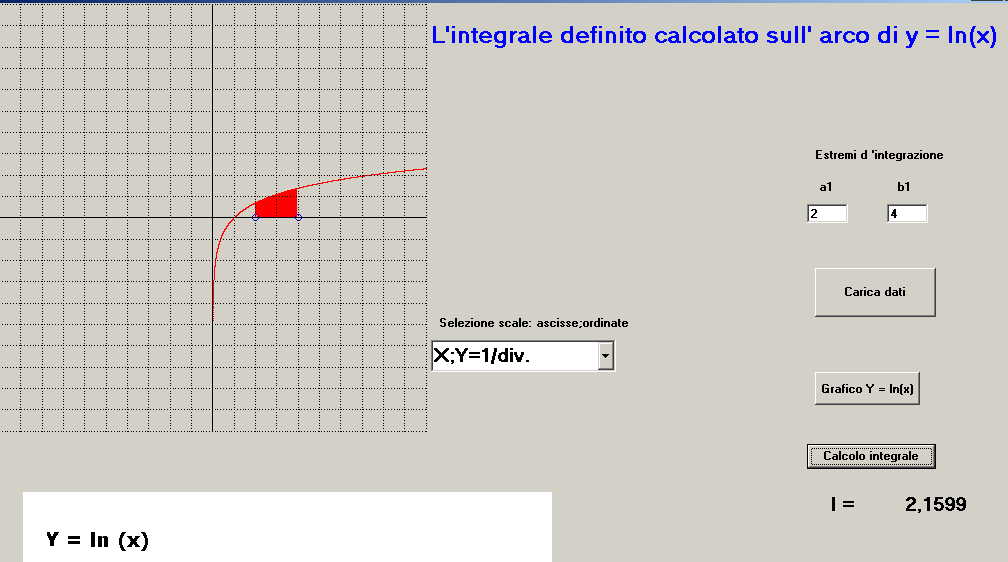figura 4 -s'impostano i valori di scala del reticolo (ad esempio x; y = 1/div )
-s'impostano gli estremi d'integrazione a1; b1 ( nell'esempio a1 = 2; b1 = 4 )
-si clicca sul pulsante "Carica dati"
-si clicca sul pulsante "Grafica y = ln (x)" e si ha il tracciato della sola funzione logaritmica,
se questo non è commisurato con le impostazioni del reticolo si ripete l'operazione con l'impostazione più adatta.
-si clicca sul pulsante "Calcolo integrale" e si ha il tracciato della funzione logaritmica
e l'arco della curva definito da a1 e b1 evidenziato con area in rosso, in contemporanea, sotto il pulsante di calcolo integrale compare il valore di I = 2.1599
6)L'applicativo per la funzione esponenziale
Una volta selezionata, tramite l'apposito pulsante in figura 1, la funzione esponenziale se ne devono stabilire le variabili richieste dalla routine nelle apposite finestre di figura 5 :
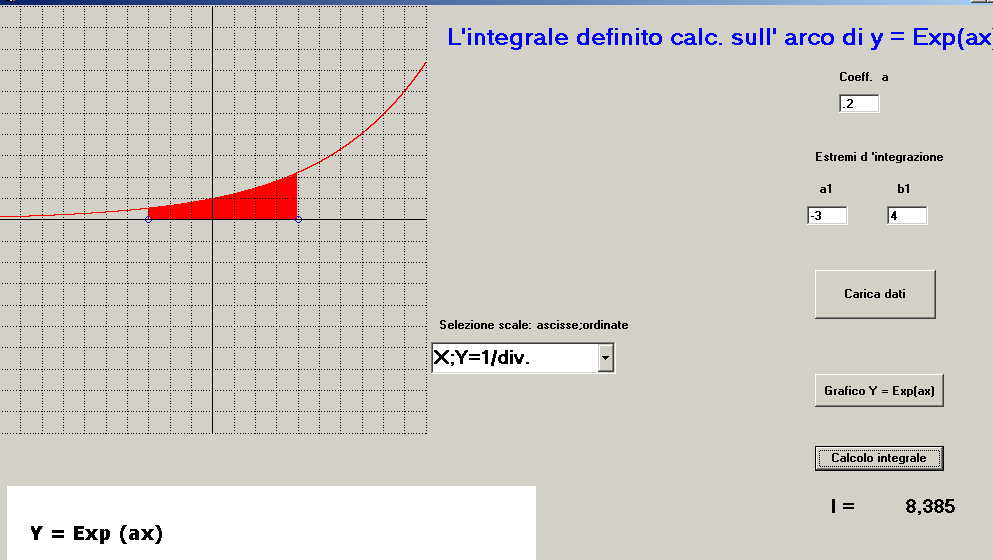figura 5 -s'impostano i valori di scala del reticolo (ad esempio x; y = 1/div )
-s'imposta il coefficiente a (ad esempio a = 0.2)
-s'impostano gli estremi d'integrazione a1; b1 ( nell'esempio a1 = -3; b1 = 4 )
-si clicca sul pulsante "Carica dati"
-si clicca sul pulsante "Grafica y = exp(x)" e si ha il tracciato della sola funzione esponenziale,
se questo non è commisurato con le impostazioni del reticolo si ripete l'operazione con l'impostazione più adatta.
-si clicca sul pulsante "Calcolo integrale" e si ha il tracciato della funzione esponenziale
e l'arco della curva definito da a1 e b1 evidenziato con con area in rosso, in contemporanea, sotto il pulsante di calcolo integrale compare il valore di I = 8.385
7)L'applicativo per la funzione seno
Una volta selezionata, tramite l'apposito pulsante in figura 1, la funzione seno se ne devono stabilire le variabili richieste dalla routine nelle apposite finestre di figura 6 :
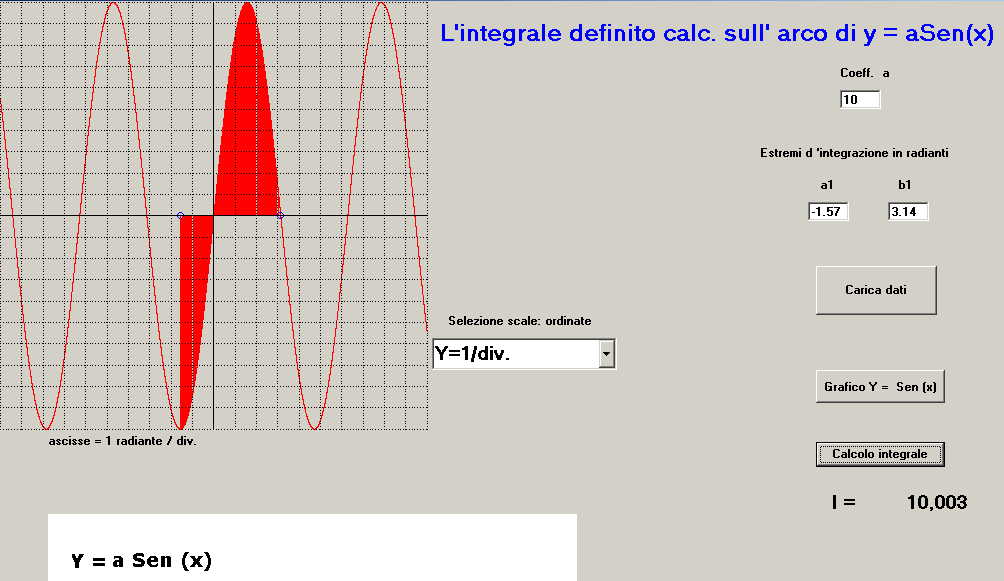figura 6 -s'impostano i valori di scala dell'ordinata del reticolo (ad esempio y = 1/div ) ; la calibrazione delle ascisse è fissa a 1 radiante/div.
-s'imposta il coefficiente a (ad esempio a = 10)
-s'impostano gli estremi d'integrazione in radianti a1; b1 ( nell'esempio a1 = -1.57; b1 = 3.14 )
-si clicca sul pulsante "Carica dati"
-si clicca sul pulsante "Grafica y = sen(x)" e si ha il tracciato della sola funzione sinusoidale,
se questo non è commisurato con le impostazioni del reticolo si ripete l'operazione con l'impostazione di y più adatta.
-si clicca sul pulsante "Calcolo integrale" e si ha il tracciato della funzione sinusoidale
e l'arco della curva definito da a1 e b1 evidenziato con area in rosso, in contemporanea, sotto il pulsante di calcolo integrale compare il valore di I = 10.003 .
Si ricorda che il valore di I calcolato è la sommatoria algebrica di due superfici, una sopra l'altra sotto l'asse x, che sono di segno opposto; se si desidera il valore assoluto della superficie evidenziata si deve ripetere l'integrazione, distintamente per i due settori da -1.57 a 0 e da 0 a 3.14, sommando quindi, in valore assoluto, i valori di I ottenuti
8)L'applicativo per la funzione sen (x) / x
Una volta selezionata, tramite l'apposito pulsante in figura 1, la funzione seno se ne devono stabilire le variabili richieste dalla routine nelle apposite finestre di figura 7 :
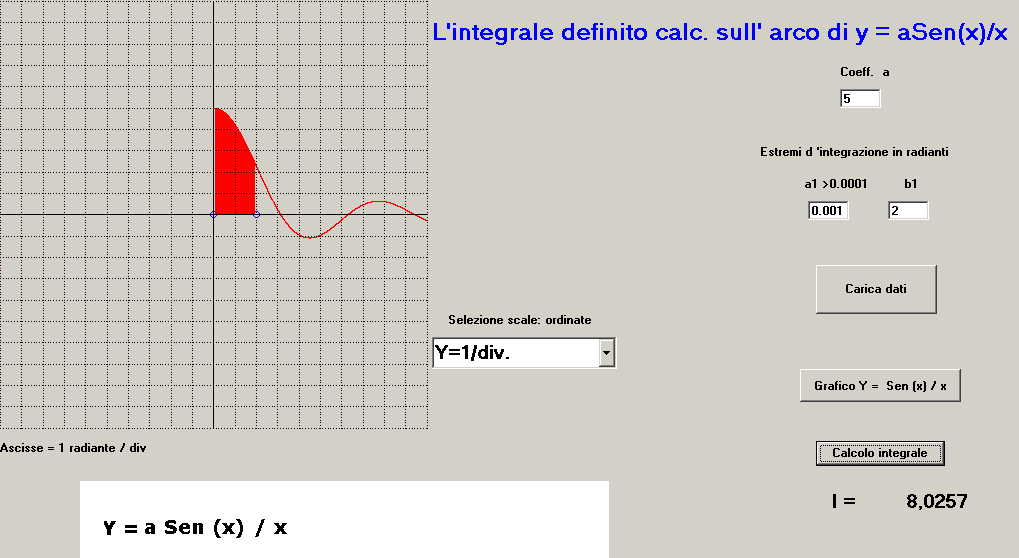figura 7 -s'impostano i valori di scala dell'ordinata del reticolo (ad esempio y = 1/div ) ; la calibrazione delle ascisse è fissa a 1 radiante/div.
-s'imposta il coefficiente a (ad esempio a = 5)
-s'impostano gli estremi d'integrazione in radianti a1; b1 ( nell'esempio a1 = 0.001; b1 = 2 ); il valore di a1, date le caratteristiche della funzione per x = 0 ; Y = 0/0) deve essere sempre a1>0.
-si clicca sul pulsante "Carica dati"
-si clicca sul pulsante "Grafica y = sen(x) /x " e si ha il tracciato della sola funzione, se questo non è commisurato con le impostazioni del reticolo si ripete l'operazione con l'impostazione di y più adatta.
-si clicca sul pulsante "Calcolo integrale" e si ha il tracciato della funzione
e l'arco della curva definito da a1 e b1 evidenziato con area in rosso, in contemporanea, sotto il pulsante di calcolo integrale compare il valore di I = 8.0257 .
9)L'applicativo per la funzione gaussiana
Una volta selezionata, tramite l'apposito pulsante in figura 1, la funzione seno se ne devono stabilire le variabili richieste dalla routine nelle apposite finestre di figura 8 :
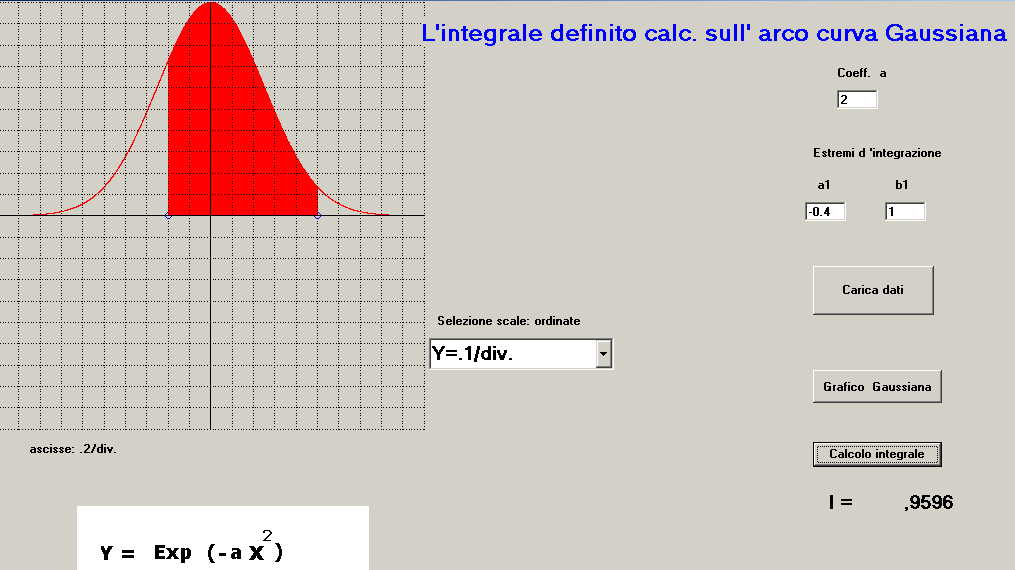figura 8 -s'impostano i valori di scala dell'ordinata del reticolo (ad esempio y = 0.1/div ) ; la calibrazione delle ascisse è fissa a 0.2 / div.
-s'imposta il coefficiente a (ad esempio a = 2)
-s'impostano gli estremi d'integrazione a1; b1 ( nell'esempio a1 = -0.4; b1 = 1 )
-si clicca sul pulsante "Carica dati"
-si clicca sul pulsante "Grafica gaussiana " e si ha il tracciato della sola funzione,
se questo non è commisurato con le impostazioni del reticolo si ripete l'operazione con l'impostazione di y più adatta.
-si clicca sul pulsante "Calcolo integrale" e si ha il tracciato della funzione e l'arco della curva definito da a1 e b1 evidenziato con area in rosso, in contemporanea, sotto il pulsante di calcolo integrale compare il valore di I = 0.9596 .
10)L'applicativo per la funzione polinomiale
Una volta selezionata, tramite l'apposito pulsante in figura 1, la funzione polinomiale se ne devono stabilire le variabili richieste dalla routine nelle apposite finestre di figura 9 :
figura 9 -il valore di scala dell'ordinata del reticolo è fissa e pari a 0.1/div
-la calibrazione delle ascisse è fissa a 0.2 / div. la curva è centrata su Xc = 5
-s'imposta il coefficiente a (ad esempio a = 0.6) il valore determina l'ampiezza dell'ondulazione sul massimo
-s'impostano gli estremi d'integrazione a1; b1 ( nell'esempio a1 = 4; b1 = 5 )
-si clicca sul pulsante "Carica dati"
-si clicca sul pulsante "Grafica polinomiale " e si ha il tracciato della sola funzione
-si clicca sul pulsante "Calcolo integrale" e si ha il tracciato della funzione
e l'arco della curva definito da a1 e b1 evidenziato con area in rosso, in contemporanea, sotto il pulsante di calcolo integrale compare il valore di I = 0.9258 .