SONAR-INFO-p189
Il calcolatore RACUBIC 1) Prefazione 2) Come si presenta l'equazione di 3° completa 3)La filosofia del RACUBIC 4) Il pannello d'impostazione e calcolo e le caratteristiche del RACUBIC 5) Come si visualizza la 3) nel reticolo cartesiano ) 6) RACUBIC: esempio d'impiego n°1 7) RACUBIC: esempio d'impiego n°2 8) La necessità dell'indicatore (8) di figura 1 9) Altro caso per l'indicatore (8) di figura 1 10) Sul comando (4) di figura 1 , slitta verticale 11) Sul comando (2) di figura 1 , selettore a bottoni 12) Ossevazioni sulla pagina p189
Per il calcolo veloce delle radici reali dell'equazioni di 3°
Questa pagina è dedicata all'impiego del file eseguibile RACUBIC.exe con
il quale computare velocemente le radici reali di un'equazione di 3°.
L'applicazione ha solo interesse tecnico e non matematico dato che non computa le radici immaginarie
dell'equazioni citate.
Prima delle istruzioni per l'impiego di RACUBIC iniziamo facendo alcune considerazioni sulle equazioni
di 3° e sui diversi percorsi di analisi matematica impiegati per risolverle.
L'equazione in oggetto ha la forma canonica sotto illustrata:
 1)
1)
Per consentirne la soluzione con le formule del CARDANO la si deve trasformare,
posto x = y - ( b / 3a ), la 1) nella nuova equazione in y mancante il termine di II° sotto esposta:
 2)
2)
La soluzione della 2), con carta e penna, presenta sensibili difficoltà; in particolar modo se
questa ha tre radici reali il procedimento di risoluzione analitica è molto complicato;
infatti conduce alle radici reali tramite il computo di radici complesse.
Ora se da un punto di vista prettamente didattico questo percorso sia di indubbia validità
per il rigore matematico, in alcune applicazioni di carattere tecnico è necessaria la risoluzione
rapida della 1) senza il computo delle radici immaginarie.
Lo scopo e raggiungibile con il file RACUBIC che viene ora illustrato.
Il file RACUBIC utilizza un metodo di calcolo misto: grafico-numerico:
grazie alla trasformazione della 1), da equazione in x a funzione di x, così come mostrato dalla 3):
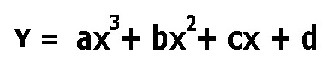 3)
3)
consente il tracciamento grafico di quest'ultima evidenziano quindi i passaggi per lo zero
indicativi delle soluzioni reali della 1).
Individuate le radici si valuta di massima entro quale intervallo delle ascisse sono collocate, indi
regolando un apposito cursore sull'intervallo anzidetto si passa alla fase automatica di computazione
sviluppata da una particolare routine di calcolo iterativo.
La routine porta alle sole radici reali della 1)
comprese nella zona selezionata entro la quale computa matematicamente l'ascissa di passaggio corrispondente ad una radice della 1).
X1 (in caso di una sola radice reale) o in X1;X2;X3 (nel caso di tre radici reali)
tutto ciò in successione.
Il pannello d'impostazione e calcolo della 1) si presenta come mostrato in figura 1 dove alcuni
numeri in rosso identificano le diverse funzioni operative:
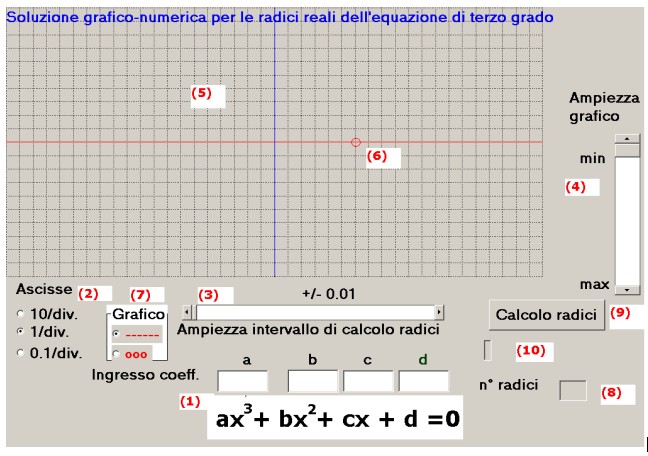
figura 1
In ordine abbiamo:
(1) ingresso per l'inserimento dei 4 coefficienti della 1):(a; b; c; d)
(2) pulsanti di selezione scala ascisse, ad es. 0.1/div (ciascun quadretto del piano cartesiano vale 0.1 in ascisse
(3) impostazione dell'intervallo di calcolo delle radici della 1) da +/- 0.01 ad +/- 1
rispetto al valore puntato dall'indicatore (6)
(4) cursore per l'incremento verticale del grafico della 3)
(5) piano cartesiano di presentazione della funzione 3) sostitutiva della 1)
(6) puntatore circolare governato dal mouse per la selezione radice da calcolare
(7) selettore del tipo di traccia per il grafico della 3)
(8) indicatore automatico del numero delle radici reali della 1)
(9) pulsante di calcolo radici
(10)indicatore numerico dei valori delle radici calcolate
Le caratteristiche del calcolatore:
Il RACUBIC è stato dimensionato per la soluzione di equazioni di 3° che abbiano radici reali
comprese in un intervallo numerico massimo di +/- 180.
Per consentire un migliore apprezzamento delle posizioni delle radici la scala grafica è selezionabile
in ascisse con: 10/div. ; 1/div. ; 0.1/div; al lancio del programma la scala delle
ascisse è sempre di 1/div. anche se non selezionata.
Naturalmente la 3) mostra come per: a = 0; b = 0 si possano risolvere equazioni di grado inferiore.
La possibilità di valutare due radici vicine è limitata ad un intervallo di circa 0.1
Per evidenziare al meglio le posizioni delle radici è previsto un moltiplicatore dell'ampiezza
del grafico da 100 volte.
Il grafico della 3) compare e si sviluppa automaticamente nel reticolo cartesiano mano a mano
che i coefficienti della 1) vengono digitati nella apposite sezioni.
La precisione di calcolo è di circa 2/10000.
La procedura base per l'impiego di RACUBIC è la seguente:
*al lancio dell'eseguibile il selettore di scala (2) è su 1/div.
*si digitano i quattro coefficienti, a; b; c; d; in (1)
*si osserva la curva che si presenta nel reticolo (5) per stabilire l'ampiezza dell'intervallo di calcolo
*si regola l'ampiezza dell'intervallo di calcolo con la slitta (3)
*con il mouse si punta la prima radice da calcolare apponendo sul passaggio per lo zero
la marca rossa (6)
*si preme il pulsante di calcolo (9)
*si attende la comparsa del valore della prima radice calcolata sul label (10)
Si possono presentare diverse curve caratteristiche di 3° grado disposte sia nei quadranti
superiori che inferiori sia in entrambi contemporaneamente; ad esempio:
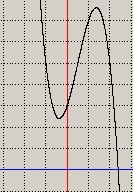
figura 2-
La curva ha il massimo relativo sul primo quadrante ed il minimo relativo nel quarto quadrante,
attraversa le ascisse
nel punto corrispondente all'unica radice reale positiva della 1)

figura 3-
La curva ha il massimo relativo nel secondo quadrante ed il minimo relativo nel terzo quadrante, attraversa le ascisse
nel punto corrispondente all'unica radice reale negativa della 1)
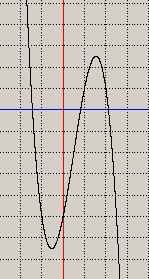
figura 4-
La curva ha il massimo relativo sul primo quadrante ed il minimo relativo sul terzo quadrante,
attraversa le ascisse
nei punti corrispondenti alle tre soluzioni della 1) ; una radice negativa e due radici positive.
Come si evince dalle figure 2; 3; 4; le ""soluzioni della 1)"", valutate in modo estremamente grossolano,
sono possibili misurando i valori delle ascisse del grafico nei punti di passaggio.
Questo sarebbe il massimo possibile se l'analisi della 1) fosse sviluppato soltanto per via geometrica
e non con il processo numerico caratteristico del RACUBIC che andremo ad esaminare.
Il primo esempio richiede alcune predisposizioni sul pannello operativo oltre l'inserzione
dei quattro coefficienti della 1) e, successivamente, l'individuazione e il calcolo delle radici interessate.
Per fare quanto proposto costruiamo ad arte un'equazione di 3° della quale conoscere a priori i
valori delle radici per valutare la precisione di calcolo del RACUBIC:
Con il prodotto di tre binomi uguagliato a zero: ( x - 1 ) ( x + 1 ) ( x + 2 ) = 0 abbiamo l'equazione
di 3°:
secondo la 1):
X^3 + 2 X^2 - x - 2 = 0
dove a = 1; b = 2; c = -1; d = -2
questa è, evidentemente, un'equazione con tre radici reali : x1 = 1; x2 = -1; x3 = - 2.
ovvero secondo la 3):
Y = X^3 + 2 X^2 - x - 2
Si eseguono le seguenti predisposizioni sul pannello:
a) s'inseriscono su (1) i coefficienti: a = 1; b = 2; c = -1; d = -2.
b) si dispone il selettore di scala (2) su 1/div.
La figura 5 mostra come si presenta la curva caratteristica nel piano cartesiano secondo la 3)
dopo le predisposizioni:

figura 5
Il grafico mostra chiaramente che l'entità delle radici è già in grado di essere valutata a vista
dato che esiste, oltre che il condizionamento a priori della loro conoscenza, il fatto che queste coincidono
con punti individuati con esattezza dal reticolo.
Indipendentemente da queste favorevoli condizioni andiamo a calcolare le tre radici; il calcolo
iterativo prevede inizialmente di stabilire un'ampiezza dell'intervallo di calcolo, slitta (3),
che consenta la non interferenza del puntatore circolare tra le tre radici compatibilmente con
il minimo valore dell'intervallo stesso per ridurre il tempo di calcolo; si stabilisca +/- 0.5.
Puntata la prima radice a sinistra, X3; inizia, premuto il pulsante (7), il "Calcolo radici", seguirà
poi la procedura per le altre due radici.
il risultato è mostrato in figura 6:

figura 6
Il risultato è :
X3 = -1.999666999 invece di -2 con un errore di circa 0.15 ‰.
Ripetendo il calcolo, puntando rispettivamente su X2 e X1 il risultato é:
X2 = -0.999501 invece che -1 con un errore di circa 0.15 ‰
X1 = 1.000166 invece che 1 con un errore di circa 0.15 ‰
Anche il secondo esempio richiede alcune predisposizioni sul pannello operativo oltre l'inserzione
dei quattro coefficienti della 1) e, successivamente, l'individuazione e il calcolo delle radici interessate.
Per fare quanto proposto costruiamo ad arte un'equazione di 3° della quale conoscere a priori i
valori delle radici, questa volta con coefficienti decimali sempre per valutare la precisione di
calcolo del RACUBIC:
Con il prodotto di tre binomi uguagliato a zero: ( x - 1.1 ) ( x + 1.1 ) ( x + 2 ) = 0 abbiamo l'equazione
di 3°:
secondo la 1):
X^3 + 2 X^2 - 1.21 x - 2.42 = 0
dove a = 1; b = 2; c = -1.21; d = -2.42
questa è, evidentemente, un'equazione con tre radici reali : x1 = 1.1; x2 = -1.1 ; x3 = - 2.
ovvero secondo la 3):
Y = X^3 + 2 X^2 - 1.21 x - 2.42
Si eseguono le seguenti predisposizioni sul pannello:
a) s'inseriscono su (1) i coefficienti: a = 1; b = 2; c = -1.21; d = -2.42.
b) si dispone il selettore di scala (2) su .1/div.
c) si posiziona il cursore orizzontale (3) per coprire un intervallo di calcolo di +/-0.2
La figura 7 mostra come si presenta la curva caratteristica nel piano cartesiano secondo la 3)
e qual'è la prima radice calcolata:
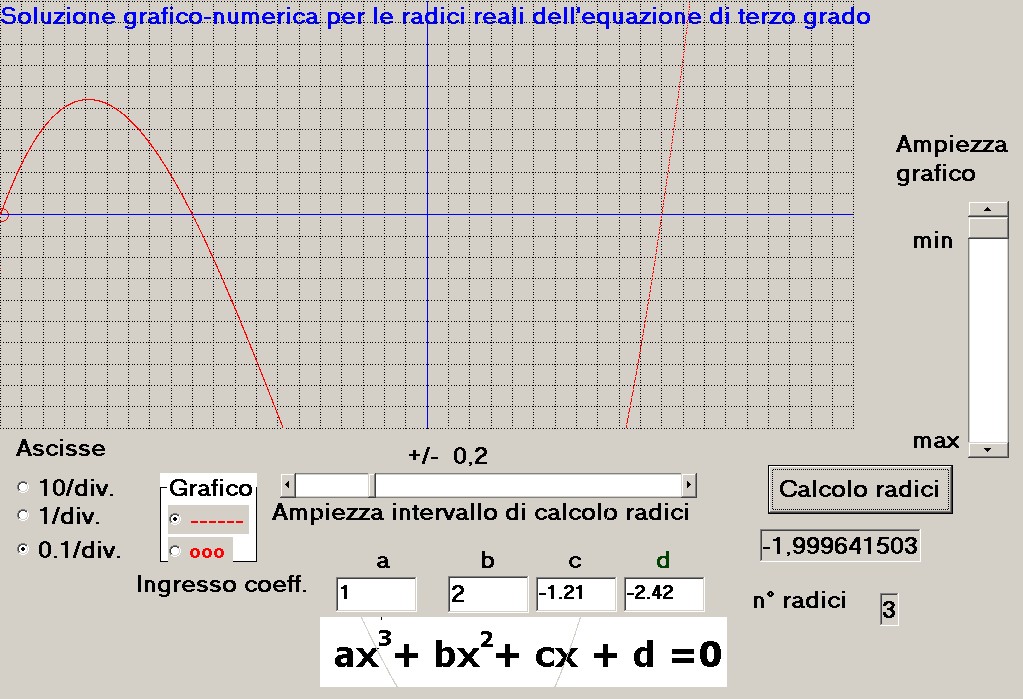
figura 7
Come si vede da figura 7 il risultato del calcolo è:
X3 = -1.999641503 invece di -2 con un errore di circa 0.15 ‰.
In modo analogo si valutano le altre radici ottenendo analoghe precisioni.
L'indicatore in oggetto, n° radici", fornisce automaticamente, a seguito di un computo molto elaborato,
una volta inseriti i coefficienti a; b; c; d; della 1), il numero delle radici reali che caratterizzano la 1) stessa;
una o tre radici.
Visti i due esercizi precedenti, nei quali il numero delle radici era deducibile osservando il grafico
della 3), si può ritenere inutile l'indicazione dell' "8" ma vedremo che così non è; anzi è da ritenersi
indispensabile quando, a seguito dei valori dei coefficienti l'ampiezza della 3) raggiunge valori talmente
elevati che non ne consentono la tracciabilità normale salvo l'impiego di tempi da calcolo improponibili.
Prendiamo in esame l'equazione 3 X^3 + 2 X^2 -2 x + 6 = 0, inseriamo i coefficienti in RACUBIC e
otteniamo il grafico di figura 8:
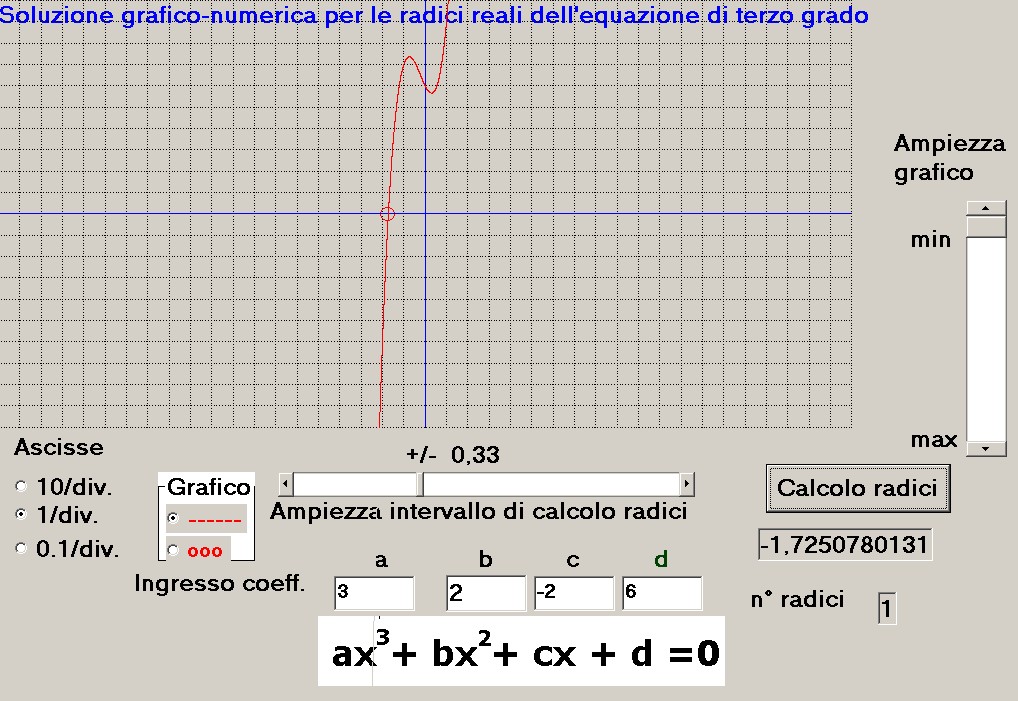
figura 8
Il grafico mostra chiaramente la presenza di una sola radice peraltro indicata dall'(8);
se il coefficiente "d" dell'equazione data
fosse uguale a 600 in vece che 6 ( lo potete provare dal vivo ) il grafico si presenterebbe senza alcuna
traccia della funzione 3) dato che la pendenza di tale traccia richiederebbe
un numero di punti di elaborazione, per il grafico ed i calcoli, talmente elevato da rallentare il
processo di grafica e calcolo rendendo impossibile l'uso del RACUBIC.
Ecco quindi che l'indicazione dell'(8) diventa indispensabile per conoscere l'esistenza della radice
dell'equazione data.
A questo punto, vista l'esistenza di una radice si tratta d'individuarla, sempre ché sia contenuta
nell'intervallo +/- 180 come da specifica del RACUBIC.
Per l'individuazione della radice si ricorre al comando (7) di figura 1 con il quale al posto di una
traccia continua si presenta una traccia indicativa con piccoli cerchietti in grado di mettere in
evidenza, di massima, la zona di passaggio della traccia per l'asse x, questo consente di scegliere
l'intervallo di calcolo e procedere ad esso così come mostra la figura 9:
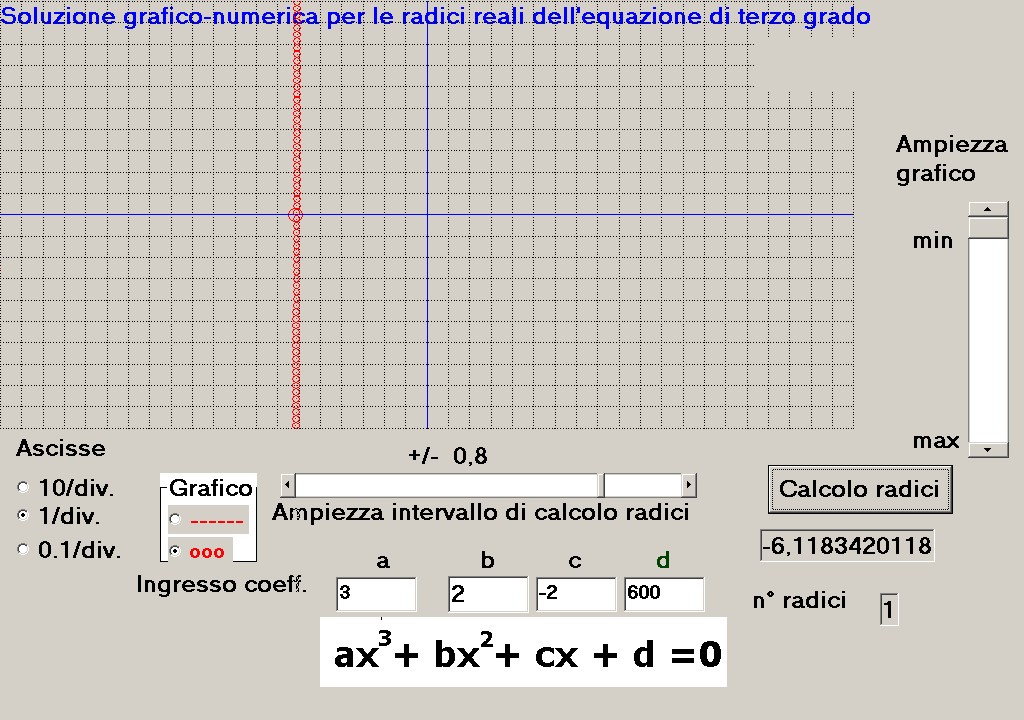
figura 9
Prendiamo in esempio l'equazione X^3 + 2 X^2 - x - 2 = 0, inseriamo i coefficienti in RAQUBIC
ed otteniamo il grafico di figura 10 con l'indicazione di (8) che mostra: n° 3 radici.

figura 10
Se l'equazione data in precedenza avesse una diverso coefficiente "c" : X^3 + 2 X^2 -1000 x -2 = 0, il grafico
non sarebbe visibile per le ragioni già esposte al paragrafo 8) mentre l'indicatore (8) ne
denuncerebbe la presenza; se queste radici sono contenute nell'intervallo di +/- 180, agendo
sul comando "grafica" (7) se ne evidenzia la presenza e la conseguente possibilità di valutarne le tre
radici reali così come mostra la figura 11:

figura 11
Il comando citato è utile per amplificare il tracciato senza alterare i passaggi per gli
zeri, ovvero non influisce sul calcolo delle radici.
Prendiamo in esame la figura 12 che mostra, attorno all'ordinata zero, l'ondulazione caratteristica
delle funzioni di terzo grado, in questo caso, viste le modeste oscillazioni, non è agevole posizionare
il puntatore circolare sulle radici da calcolare; non resta che agire sul comando (4) per passare da
figura 12
a figura 13 dove le condizioni di puntamento sono decisamente migliorate:
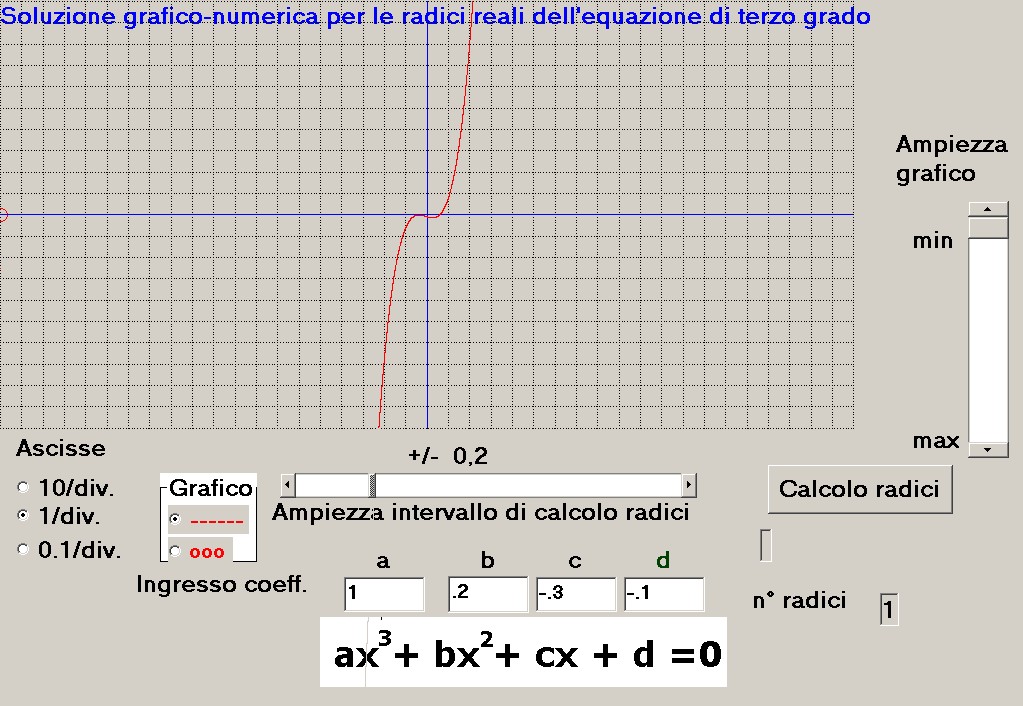
figura 12

figura 13
Con il selettore in oggetto si possono variare le ascisse di presentazione dei grafici in tre scale
0.1/div. 1/div. 10.div.
Al lancio del programma il RACUBIC è predisposto su scala 1/div.
Supponiamo che si debba risolvere l'equazione : X^3 + 0.001 X^2 - 0.25 X - 0.0002, in questo caso dopo
l'inserimento
dei 4 coefficienti, si ha la presentazione grafica di figura 14 che mostra la difficoltà
nel puntamento delle posizioni delle tre radici; a questo punto non resta che selezionare la scala
espansa di 0.1/div. per ottenere il grafico di figura 15 sul quale operare con facilità per la soluzione dell'equazione data:
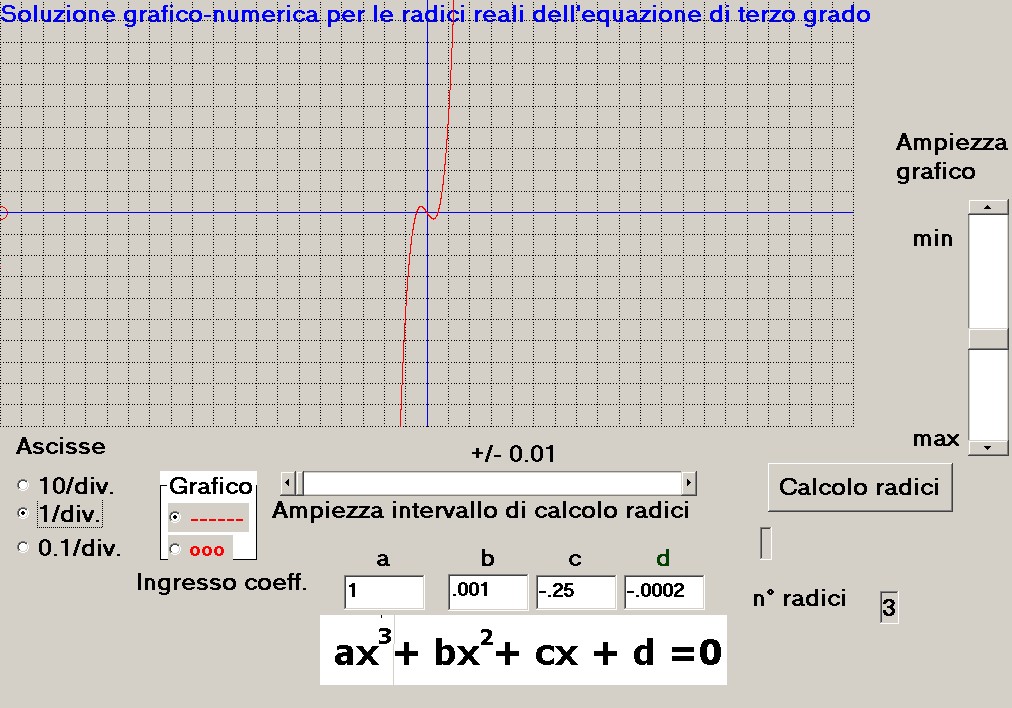
figura 14
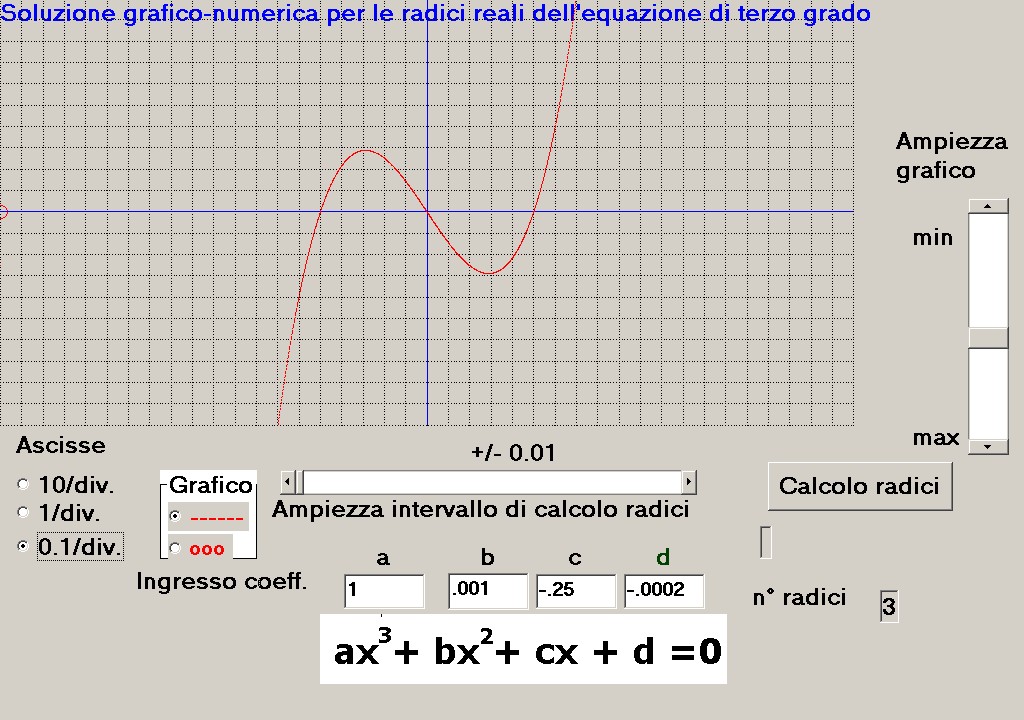
figura 15
Il programma sorgente che ha generato RACUBIC è molto complicato; è pertanto possibile che
qualche piccola anomalia si presenti durante l'uso.
In tal caso siete pregati di darne notizia tramite il link "Contatti" del sito, sarà mia cura rivedere
il programma e ripubblicare la versione corretta.
Si fa presente che i programmi sorgente sono sviluppati in Visual Basic 5 e che, sempre
con lo stesso strumento, vengono generati i file eseguibili; per tale ragione
gli eseguibili sono esenti da virus.
Purtroppo alcuni Antivirus scartano a priori qualsiasi eseguibile che non sia già stato testato!!!
è il cane che si mangia la coda, in tal caso e meglio ricorre a qualche P.C. datato non soggeto
di tanto scrupolo.