1) GENERALITA'
Nella fase successiva alla progettazione del FALCON (vedi p4) è stata di fondamentale importanza la simulazione numerica dei segnali, dei rumori e dell'algoritmo di correlazione con le matrici di calcolo; un processo così complesso non poteva essere messo fisicamente in opera senza l'appoggio di una dimostrazione matematica che garantisse il conseguente risultato positivo dell'impresa.
Dato che una delle caratteristiche salienti dei sistemi di correlazione tra segnali coerenti a due stati si configura nella dipendenza dell'ampiezza della funzione di correlazione, Crt, dal rapporto Si/Ni all'ingresso del dispositivo (si veda p5 ;cap.4; par.4.3) secondo l'espressione:



anche l'elaborazione con matrici di calcolo del FALCON avrebbe dovuto rispettare la citata legge.
L'implementazione della funzione Crt = f(Si/Ni) in un programma in Visual Basic è abbastanza semplice, più complesso è lo sviluppo del software di simulazione dei segnali, dei rumori, e di controllo della struttura a matrici del FALCON che opera contemporaneamente su quattro coppie di segnali idrofonici.
Nel prosieguo della pagina vedremo come implementare in VB le routine di simulazione citate.

2) I SEGNALI ED I RUMORI CHE IL FALCON DEVE ELABORARE SIMULTANEAMENTE
La formazione di un fascio di direttività FALCON impiega 4 coppie di segnali idrofonici così come mostra la figura 7 riportata nel progetto generale illustrato in p4:



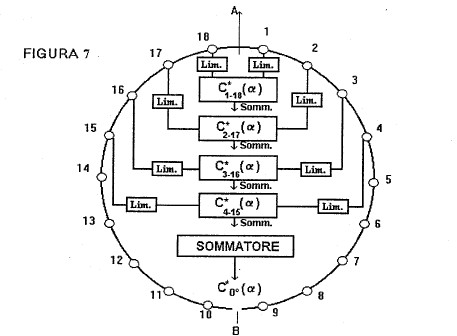
La simulazione software degli otto segnali e dei rumori che li inquinano deve pertanto generare 4 coppie di segnali con rumori; i segnali di ciascuna coppia sono coerenti tra loro, ma incoerenti con i segnali delle altre coppie, mentre gli 8 rumori che li inquinano sono tra loro tutti incoerenti, in altri termini:
la coppia (S1 + N1) e (S18 + N18), ad esempio, ha S1 coerente con S18 e N1 incoerente con N18.

3)LO SCHEMA A BLOCCHI DELL'INTERO PROCESSO DI SIMULAZIONE
In figura 2 è tracciato lo schema a blocchi di tutto il processo di simulazione così numerato:
1) Calcolo e tracciamento funzione di riferimento Crt = f(S/N)
2) Generazione della matrice di correlazione
3) Generazione di 8 segnali analogici di rumore scorrelati tra loro
4) Generazione di 4 coppie di segnali analogici, gli elementi di ciascuna coppia sono coerenti
5) Composizione delle 4 coppie di segnali affette da rumore
6) Trasformazione delle coppie analogiche del punto precedente in coppie digitali ( segnali a due stati )
7) Generazione della stringa d'interrogazione matrice di correlazione
8) Uscita matrice e processo d'integrazione numerica
9) Tracciamento della funzione risultato della simulazione



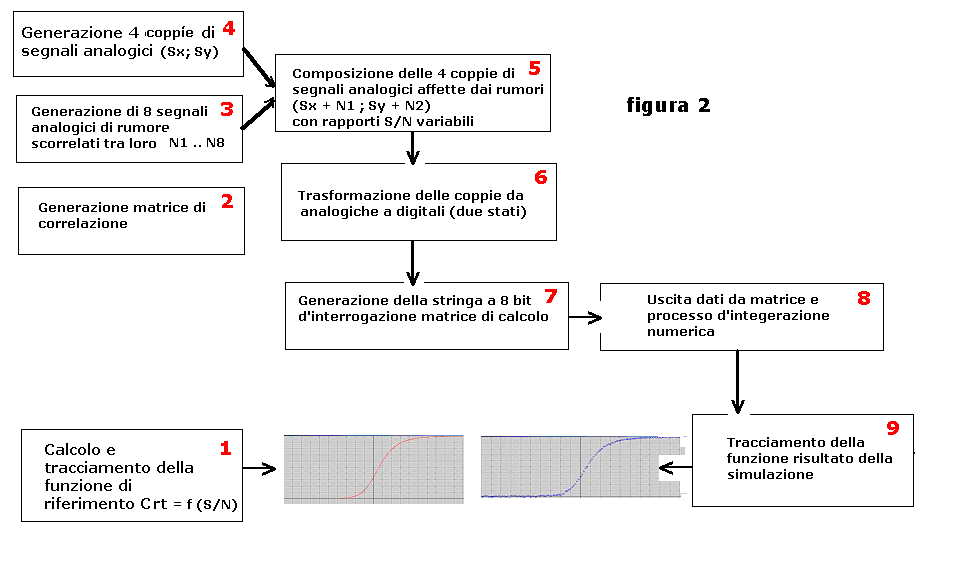
A seguito dello schema a blocchi la descrizione del software distintivo di ciascun blocco.

4) BLOCCO 1
-SOFTWARE DI CALCOLO E IL TRACCIAMENTO DELLA FUNZIONE DI RIF. Crt = f(SI/NI)
4.1)Costruzione del reticolo per la presentazione grafica
Tra le innumerevoli possibilità di tracciamento del sistema cartesiano di presentazione è stata implementata la seguente routine che non commenteremo:

Sub reticolo' routine per il reticolo cartesiano
For xi = 0 To 4600 * 2 Step 230 * 2
For yi = 0 To 3200 * 2 Step 20 * 2
PSet (xi, yi)
Next yi
Next xi
For yi = 0 To 3200 * 2 Step 160 * 2
For xi = 0 To 4600 * 2 Step 30 * 2
PSet (xi, yi)
Next xi
Next yi
Line (0, 1600 * 2)-(4600 * 2 + 160, 1600 * 2)
Line (4600, 0)-(4600, 3200 * 2)
End Sub 'fine routine


4.2)ROUTINE PER IL CALCOLO DELLA Crt = f(SI/NI) TEORICA.
L'espressione riportata in 1), variabile da 0 ad 1 per S/N variabile da -60 dB a +60 dB, è così implementata:

Private Sub Command1_Click() 'esegue il calcolo e la presentazione grafica a comando di un pulsante
For sn = -60 To 60 Step 0.1 'impostazione della variabile (Si/Ni) nel campo -60dB +60dB a passi di 0.1 dB
sk = sn + 60 ' variabile per la grafica delle ascisse
t = 1 / (1 + (1 / (10 ^ ((sn) / 20)) ^ 2)) 'calcolo del Seno
arc = Atn(t / Sqr(-t * t + 1)) 'calcolo dell'arco
Su = (2 / 3.14) * arc 'calcolo della funzione Crt = f (Si/Ni)
PSet (9200 * sk / 120, 3200 - 3200 * Su), vbRed 'traccia la Crt=f(Si/Ni)
Next
End Sub' fine della routine
La curva teorica di Crt = f (S/N) è riportata in figura 3:

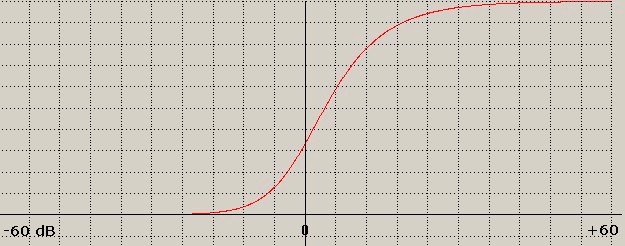figura 3

5) BLOCCO 2
- IL SOFTWARE PER LA GENERAZIONE DELLA MATRICE DI CORRELAZIONE
La routine è sotto riportata e commentata:

Dim I(255) 'dimensione tabella corr. idrofoni
Private Sub Form_Load()
For x = 0 To 255
Y1 = x And 15 'si isolano i 4 bit msb
Y2 = x And 240 'si isolano i 4 bit MSB
y3 = Int(Y2 / 16) 'si spostano i 4 bit MSB in posizione msb
'si capolge y3 per eseguire xor con y1
y4 = Int((y3 And 1) * 8) + Int((y3 And 2) * 2) + Int((y3 And 4) / 2) + Int((y3 And 8) / 8)
y5 = Abs((Y1 Xor y4) - 15) 'si esegue xor tra y1 e y4 (-15 per coinc. =1)
'si sommano aritmeticamente le coincidenze ottenute da xor y1 e y4
'si ottiene il numero del peso : 0,1,2,3,4
y6 = (y5 And 1) + ((y5 And 2) / 2) + ((y5 And 4) / 4) + ((y5 And 8) / 8)
I(x) = y6 'scrive in memoria le corrispondenze(TABELLA) tra il valore di
'x(dato di entrata) e il valore y6 corrispondente al peso di correlazione
Next x
End Sub

6) BLOCCHI 3/4/5
- LA GENERAZIONE DELLE 4 COPPIE DI SEGNALI ANALOGICI + RUMORE
Si sviluppano 4 routine, una per coppia di segnali, del tipo:

Randomize Timer
j = 10 ^ (sn / 20) 'CALCOLO Si/Ni come numero puro " j "
'GENERAZIONE PRIMA COPPIA SEGNALI E DISTURBI IN FORMA ANALOGICA
k1 = Rnd
k2 = Rnd
k3 = Rnd
k4 = Rnd
k5 = Rnd
k6 = Rnd
k7 = Rnd
k8 = Rnd
k9 = Rnd
nl1a = k1 + k3 + k5 + Rnd - 2 'rumore scorrelato nl1
nl2a = k2 + k4 + k6 + Rnd - 2 'rumore scorrelato nl2
yoa = k7 + k8 + k9 + Rnd - 2 'sorgente del segnale
y1a = yoa * j + nl1a 'primo segnale + disturbo
y2a = yoa * j + nl2a 'secondo segnale + disturbo

7) BLOCCO 6
- LA TRASFORMAZIONE DELLE 4 COPPIE DI SEGNALI + RUMORE DA ANALOGICHE A DIGITALI
Si sviluppano due righe di programma per coppia:

'TRASFORMAZIONE SEGNALI+DISTURBI "A" IN DUE STATI 1 or 0
If y1a < 0 Then s1a = 1 Else s1a = 0 's1a=1^segnale coppia A
If y2a < 0 Then s2a = 1 Else s2a = 0 's2a=2^ segnale coppia A

8) BLOCCO 7
- LA CREAZIONE DELLA STRINGA D'INTERROGAZIONE MATRICE
'CONVERTE IL DATO BINARIO A 8 BIT FORMATO DALLE 4 COPPIE s1x-s2x IN DECIMALE

y = 128 * s2d Or 64 * s2c Or 32 * s2b Or 16 * s2a Or 8 * s1a Or 4 * s1b Or 2 * s1c Or s1d

9) BLOCCO 8
- INTERROGA LA MATRICE ED ESEGUE L'INTEGRAZIONE NUMERICA DEI DATI RESI
Cr = (I(y) + Cr - Cr / beta) 'CALCOLA LA FUNZIONE DI CORRELAZIONE E INTEGRA I DATI

Il valore di "beta" stabilisce la costante di tempo d'integrazione.

10)ANELLO DI CALCOLO
Tutte le routine, dalla 3 alla 8 sono vincolate ad un anello di calcolo da 20000 giri affinché per ciascun valore di S/N possa compiersi l'integrazione dati.

11)BLOCCO 9
-ANELLO DI PRESENTAZIONE FUNZIONE Crt = f(S/N)
L'anello precedente è a sua volta disposto all'interno di un anello la cui variabile è costituita dal rapporto S/N = sn variabile da -60 a + 60 dB.
Alla fine dell'anello l'istruzione:

sk = sn + 60
Circle (9200 * sk / 120, 3200 - 3200 * Su), 32, vbBlue 'per tracciare la Crt=f(Si/Ni) simulata

genera il grafico per punti della Crt virtuale così come mostrato in figura 4:

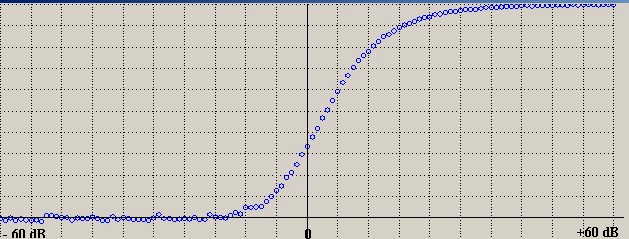figura 4

12)UN CASO A DIMOSTRARE COME IL PROCESSO FALCON SIA CONFORME ALLE ASPETATIVE TEORICHE
Sovrapponendo alla curva dovuta alla simulazione del processo FALCON la curva teorica calcolata secondo la funzione:



si ottiene l'ottimo risultato mostrato in fine in figura 5:

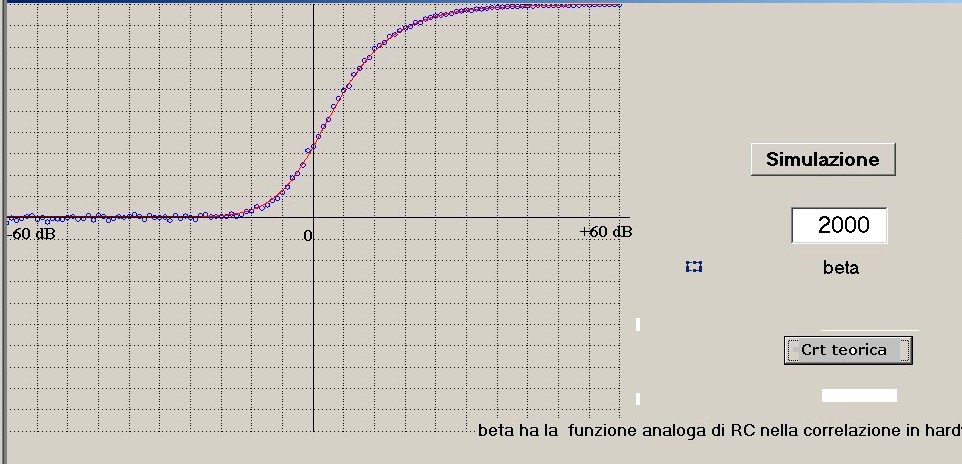figura 5

La curva teorica è tracciata in rosso, quella dovuta alla simulazione è tracciata per cerchietti blu; come si vede le due curve sono sovrapponibili salvo nella zona dove il rapporto Si/Ni è peggiore e la varianza crea le aspettate* ondulazioni della Crt simulata.


* La Crt simulata è affetta da varianza in quanto è realizzata impiegando un tempo d'integrazione finito dipendente dal valore numerico della variabile "beta".
La curva teorica invece, tracciata con l'algoritmo mostrato nel paragrafo 1), è priva di varianza perché la funzione che la definisce è ottenuta con procedimento analitico che prevede calcoli come limite delle sommatorie per un tempo infinito.