SONAR-INFO-p200
Uno degli impedimenti al soccorso dei sommergibili sinistrati 1) Generalità 2) La propagazione del suono in mare 3)Caratteristiche del modello preso ad esempio 4)Calcolo dell'andamento della velocità del suono in funzione della quota q; C = f( q ) 5) Calcolo delle traiettorie dei raggi acustici 6) Il cono d'ombra
Per la sicurezza dei sommergibili è necessario che questi siano dotati di uno o più risponditori
acustici ( si veda p161 ) in grado di emettere impulsi sonori se opportunamente interrogati con segnali
a diverse frequenze generati dai sonar dei mezzi di soccorso.
In questa pagina illustreremo uno tra gli impedimenti che ostacolano le ricezione degli impulsi
del risponditore da parte dei sonar delle navi operative.
E' noto che se l'acqua del mare, in zone non molto profonde, fosse perfettamente omogenea
e alla stessa temperatura a tutte le quote, i raggi acustici si propagherebbero per successive onde
sferiche nei primi 1000 metri di distanza dal generatore dopo di che, a seguito riflessioni dal fondo
e dalla superficie, si trasformerebbero in onde cilindriche come mostra la figura 01:
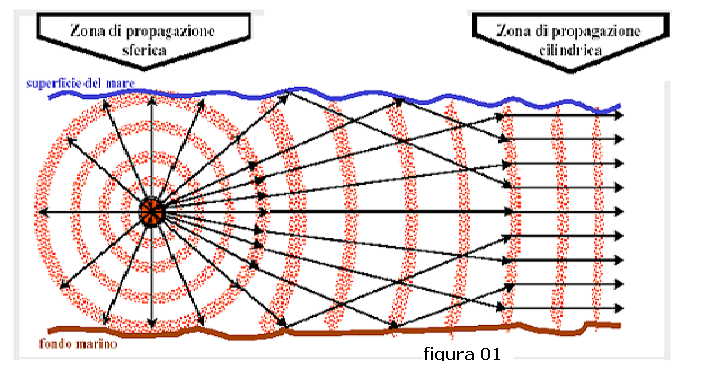
In queste condizioni ideali la trasmissione degli impulsi da parte di un risponditore
acustico non sarebbe in alcun modo ostacolata e i mezzi di soccorso localizzerebbero
con certezza il sommergibile sinistrato.
La realtà fisica del mezzo è purtroppo diversa e, come illustrato in p24-p26-p28-p30, la propagazione del suono
non segue le leggi sopra descritte ma assume le più disparate geometrie a causa della differenza
di temperatura dell'acqua alle diverse quote; un esempio significativo delle condizioni
critiche nelle fasi di scoperta degli impulsi del risponditore acustici
è riportato nel paragrafo seguente.
1- Profondità del sommergibile sinistrato ( risponditore ) q = 780 m
2- Direttività del trasduttore del risponditore = omnidirezionale
3- Raggio di ricerca da parte nave di soccorso = 10000 m
4- Profondità messa a calcolo: da q = 0 a q = 1000 m
5- Ampiezza dell'angolo verticale di calcolo = 90°
6- Numero delle tracce calcolate = 9
7- Intervallo angolare di calcolo tra le tracce = 10°
8- Tabella dei rilievi della temperatura alle diverse quote in figura 1:
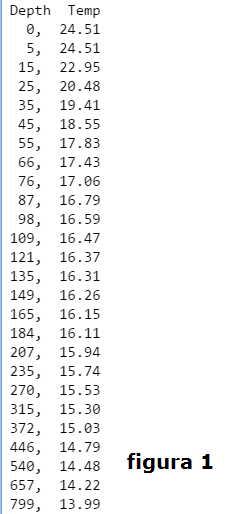
Con i dati illustrati nella tabella di figura 1 si traccia:
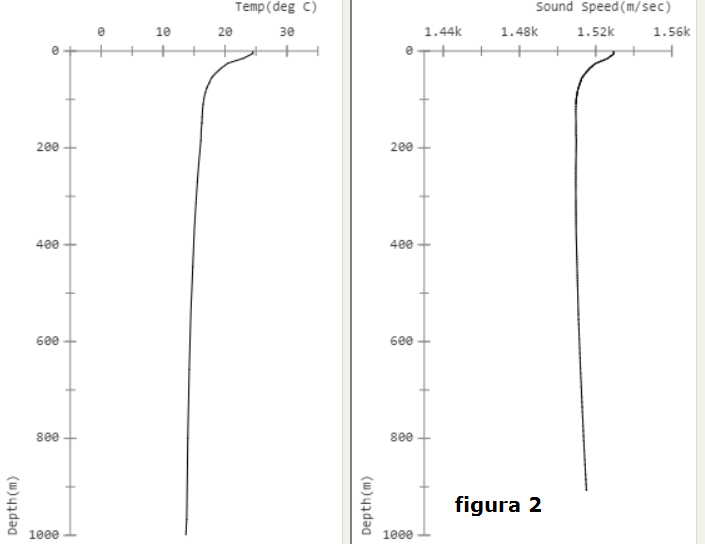
t° = f(q) come mostra la prima curva di figura 2.
Di seguito si computa la C = f(t°) secondo l'equazione:
C = 1449 + 4.6 t° + 0.055 (t°) 2 + 1.39 (S-35) + 0.016 q in m/Sec.
dalla prima curva di figura 2 e dall'equazione data si traccia la seconda curva di figura 2
che mostra l'andamento della C = f(q):
In base ai valori espressi dalla C = f (q) e mettendo a calcolo i dati impostati
in 3) si ottiene il diagramma di figura 3 che andiamo a commentare:
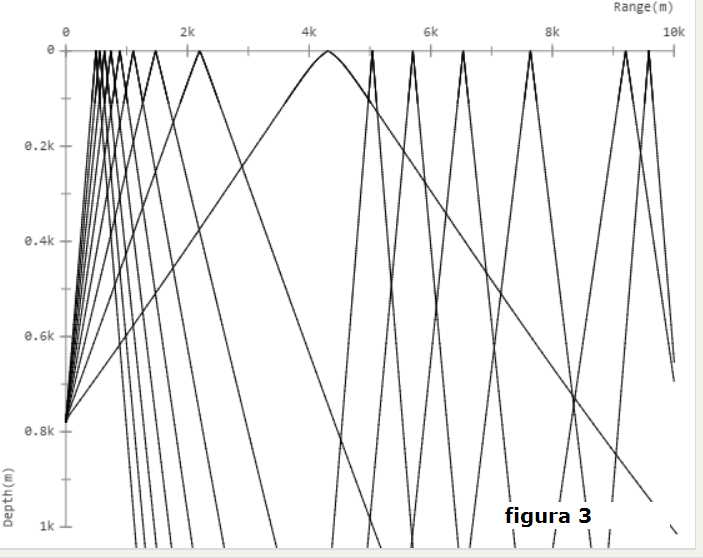
Dal lato sinistro della figura, per q = 780 m, si generano i 9 raggi che si propagano
verso la superficie; il più elevato attiene all'emissione perpendicolare al fondo ( θ = 90° )
con i successivi per ( θ = 80° ) ... ( θ = 10° ) tutti deviati verso il fondo
a seguito della variazione della velocità del suono con la quota q.
Il primo raggio incide sulla superficie del mare a circa 500 m dalla perpendicolare al
risponditore, gli altri 8 raggi e gli innumerevoli che stanno tra un raggio di calcolo
e il successivo coprono da circa 500 m in poi tutta la superficie con le attenuazioni
classiche dovute alla divergenza ed all'assorbimento.
La zona di mare compresa tra 0 e circa 500 m non viene illuminata dai raggi
acustici così come mostra la figura 3, questa situazione è mostrata in figura
4 con l'evidenza della creazione di un cono d'ombra con un diametro di ben 1000 m:
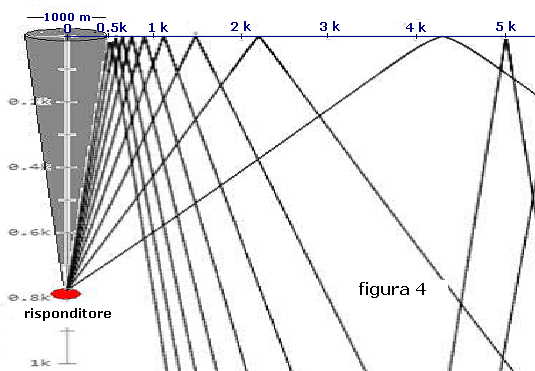
Qualsiasi mezzo di soccorso, equipaggiato soltanto con sonar di superficie , che navigasse in tale zona in
un raggio di circa 500 m dalla perpendicolare del risponditore, non riceverebbe gli impulsi emessi da quest'ultimo.
La situazione peggiorerebbe se il sommergibile sinistrato si trovasse a profondità più
elevate di quella presa ad esempio.