SONAR-INFO-p206


La struttura fine dell'equazioni del sonar attivo


1) Generalità

L'equazioni applicative del sonar attivo sono state sviluppate in forma logaritmica per semplificare il calcolo della portata del sonar, infatti l'equazioni suddette, espresse in decibel, si riducono ad una serie di somme e differenze più pratiche da impiegare.
L'impostazione citata non offre però facilità di comprensione del legame esistente tra le variabili a chi per la prima volta s'interessa dell'argomento.
Con questo lavoro vogliamo mostrare come nascono le equazioni applicative del sonar mediante l'analisi della struttura fine delle stesse.
S'inizia con un richiamo dettagliato delle equazioni citate per procedere poi alla loro analisi.
L'analisi, per renderne semplice la comprensione, è svolta in modo non rigorosamente scientifico pur salvaguardando la correttezza dei risultati finali.

2) L'equazione applicativa del sonar attivo

In tutte le pagine del sito, esclusa la presente, l'equazione del sonar attivo è stata mostrata soltanto in termini logaritmici, nella forma applicativa ( si veda p44 ), per il calcolo diretto delle caratteristiche di scoperta del sonar secondo le due espressioni:

1) TL = 120 dB + 40 Log R + 2 a R [attenuazione per divergenza sferica e assorbimento] 001)

2) TL = LI + TS + DI - NL - DT [massima attenuazione consentita] 002)

Elenchiamo di seguito, illustrandone la specificità, la serie delle variabili che consentono i calcoli di previsione delle portate di scoperta del sonar attivo (dove con ../Hz s'intende radice di Hz):

*F = la frequenza di emissione del sonar in Hz (ad es. 8000 Hz)

*LI = il livello della pressione degli impulsi emessi in dB/microPascal (ad es. LI = 200 dB/microPascal)

*NL = il rumore "spettrale" dovuto allo stato del mare in dB/microPascal/Hz (ad es. il rumore del mare a stato S = 4 "definito come mare agitato" alla frequenza di 6000 Hz è 54 dB/microPascal/Hz)

*DI = il guadagno di direttività della base trasmittente/ricevente in dB
(ad es. DI = 22 dB alla frequenza di 8000 Hz)

*t = la durata dell'impulso di emissione in Sec. (ad es. t = 0,015 Sec.)

*d = il valore, in numero puro, legato alla probabilità di scoperta e falso allarme accettata
( ad es. per d = 10 si prevede il 50% di probabilità di scoperta e lo 0.1 % di falsi allarmi)

*Propagazione = ipotesi sul tipo di propagazione- "Sferica" o "Cilindrica" -(ad es. in acque poco profonde si ipotizza prevalentemente la combinazione: sferica per i primi 1000 m e cilindrica oltre)

* R = variabile che caratterizza l'attenuazione del suono lungo il percorso in mare, espressa in Km
(ad es. da R= 0.1 Km a R = 20 Km )

*a = coefficiente d'attenuazione, in dB/Km, relativo alle caratteristiche di assorbimento del suono nell'acqua in funzione della frequenza (ad es. per f = 11000 Hz   a = 0,67 dB/Km )

*BW = banda di ricezione in Hz ( ad es. BW = 500 Hz )

* DT = soglia di rivelazione in dB; dipende da "d" , BW e t (ad es. può valere DT =10 dB)

*TS = forza del bersaglio in dB (ad es. può essere TS = 8 dB -dipende dalla forma e dalle dimensioni del bersaglio)

*TL = variabile, espressa in dB, che indica la generica attenuazione del segnale
( ad es. TL = 80 dB può essere riferito sia all'attenuazione dovuta al percorso del suono, sia all'attenuazione massima accettata in base ai parametri sopra elencati)

3) Esame dettagliato dei termini logaritmici della 001) -funzione d'attenuazione-

L'equazione 001), relativa all'attenuazione del suono nell'acqua, (TL = 120 dB + 40 Log R + 2 a R) illustrata nel paragrafo precedente discende da una serie di rapporti tra grandezze lineari che andiamo ad esaminare:

Il primo rapporto tra grandezze è relativo al calcolo dell'intensità acustica di emissione "Ie" (calcolata ad 1 m di distanza dal generatore) che, nella propagazione ideale del suono per divergenza sferica, è data da:

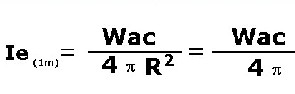1)

dove:
Wac = potenza acustica emessa dal generatore ( ipotizzato di dimensioni puntiformi )
R = distanza dal generatore in metri; dato R = 1m si ha: Ie = Wac / (4 π).

Il secondo rapporto è relativo alla pressione Ii incidente sul bersaglio posto alla distanza R:

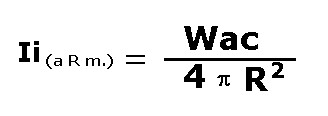2)

L'intensità acustica passa da Ie a Ii lungo la distanza R secondo l'attenuazione Att, dovuta alla divergenza sferica, che è data dal rapporto Ie/Ii come mostra la 3):

3)

Dato che nel sonar attivo il percorso del suono è di andata (impulso emesso) e ritorno (eco del bersaglio) l'attenuazione complessiva diventa:

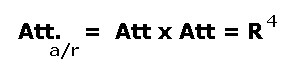4)

La 4) trasformata, per semplicità di calcolo, in termini logaritmici ( decibel ) vede il simbolo Att(a/r) assumere la forma TL secondo la 5:

5)

Nella 5) il valore di R è espresso in metri; se nella 4) la distanza R è espressa in Km la 4) diventa:
Att(a/r) = (1000 R) 4 e la 5) assume la forma:

6)

che rappresenta il primo e il secondo addendo della 001).
Nella propagazione del suono in mare una seconda causa d'attenuazione è dovuta all'assorbimento dell'energia acustica da parte del mezzo di trasmissione.
Questa attenuazione, funzione della frequenza è stata studiata da Thorp e definita dalla formula:

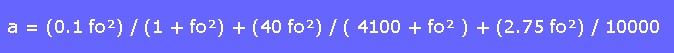7)

Nella 7) la frequenza fo è espressa in KHz ed "a" ha dimensioni logaritmiche espresse in dB / Km. L'attenuazione per assorbimento nei due sensi di percorso del suono è quindi:

Att(ass) = 2 "a" R

che rappresenta il terzo addendo della 001)

Con la 001) si computa quindi l'attenuazione dell'impulso acustico emesso dal sonar nel percorrere, avanti (impulso d'origine) e indietro (l'eco), la distanza R tra sonar e bersaglio.

4) Esame dettagliato dei termini logaritmici della 002) (funzione di massima attenuazione)

L'equazione 002) discende da una serie di rapporti e prodotti tra grandezze lineari sensibilmente più complessi di quelli relativi alla 001).
L'equazione logaritmica 002) espressa in dB, TL = LI + TS + DI - NL - DT , è relativa alla massima attenuazione dell'impulso e del conseguente eco del bersaglio accettabile in determinate condizioni operative.
Una volta che la 002) abbia lo stesso valore della 001) saranno soddisfatte le condizioni di scoperta del bersaglio secondo l'impostazione del sonar stabilita al momento contingente.
Il legame tra queste nuove grandezze è relativo al calcolo dell'attenuazione massima "tl" dalla quale discende il TL della 002), il "tl" è esprimibile con la seguente funzione di variabili lineari:

8)

nella quale il significato dei simboli è:

"tl" = massima attenuazione sostenibile dall'impulso emesso dal sonar

"li" = livello indice di trasmissione, espresso in microPascal (μPa), generato dal sonar all'atto dell'emissione dell'impulso in regime di propagazione sferica valutato ad un metro di distanza dal generatore (la base di trasmissione):

"ts" = forza del bersaglio, espressa in mq, indica la capacità di riflessione del bersaglio e ne subordina l'intensità dell'eco.

"di" = guadagno della base idrofonica ricevente, adimensionale

"nl" = livello del rumore del mare, espresso in microPascal (μPa), nell'intorno della base ricevente

"dt" = soglia di rivelazione del sonar in numero adimensionale

l calcolo di "tl" è volto a stabilire la massima attenuazione sostenibile dell'impulso emesso in andata e dall'eco di ritorno dal bersaglio con le variabili indicate nell'equazione data.
- Maggiore sarà il valore di "li" (pressione acustica dell'impulso di trasmissione) più elevata sarà la portata di scoperta
- Maggiore sarà il valore di "ts" (forza del bersaglio) più elevata sarà la portata di scoperta

- Maggiore sarà il valore del "di" (guadagno della base rice-trasmittente) più elevata sarà la portata di scoperta
- Maggiore sarà il valore del "nl" (livello del rumore del mare) minore sarà la portata di scoperta
- Maggiore sarà il valore di "dt" ( soglia di rivelazione) minore sarà la portata di scoperta

Vediamo come si computano le variabili citate:

-Calcolo di "li"
Il valore di "li" si calcola con l'espressione:

9)

dove:
li = livello dell'intensità acustica, espresso in μPa, alla distanza R = 1 m dal generatore
Wac = potenza acustica irradiata dal trasduttore in W acustici
k = coefficiente di conversione Wac in μPa
Gd = guadagno di direttività in trasmissione del trasduttore in termini lineari

se supponiamo:
Wac = 6000 Wac
Gd = 200
essendo k = 158 x 1015 μPa/Wac; alla potenza acustica irradiata corrisponderà una livello di pressione :
li = 6000 Wac X 158 x 1015 x 200 = 189.6 x 1021 μPa
Il valore di "li" è definito come livello indice di trasmissione.
Come si può osservare "li", espresso in grandezza lineare, mostra numeri molto grandi non facilmente manipolabili, di quì la necessita delle espressioni logaritmiche della 002).

-Calcolo di "ts"
Il valore di "ts" (nel caso che si assimili il bersaglio ad un cilindro) si calcola con l'espressione:

10)

dove:
r = raggio del cilindro
l = lunghezza del cilindro
f = frequenza dell'impulso incidente
c = velocità del suono ( 1500 m/Sec. )
nel caso che siano: r = 1 m; l = 2 m; f = 7500 Hz si ha ts = 10 mq

-Calcolo del "di"
Il valore del "di" per base equivalente piana è dato da:

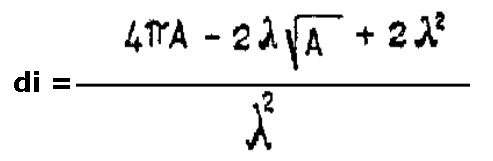11)

dove:
A = superficie della base in mq
λ = 1530 / f
nel caso che siano A = 1 mq ; f = 7500 Hz si ha "di" = 294

-Calcolo di "nl"
Per il calcolo di "nl" si assume uno stato del mare SS = 4 a 7500 Hz al quale corrisponde:
"nl" = 158.4 x 103 μPa (si veda p58)

-Calcolo di "dt"
Il valore del "dt" si calcola con l'espressione:

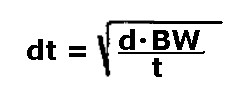12)

dove:
d = coefficiente legato a Priv. e Pfa. ( si veda p 84 )
BW = banda di ricezione del sonar
t = lunghezza impulso d'emissione
Nel caso in esempio: per d = 9; BW = 600 Hz; t = 10 mSec. si ha dt = 735

5) Passaggio dalla funzione lineare 8) alla 002)

Per il passaggio dalla funzione lineare 8) alla 002) in forma logaritmica, trasformando i termini della prima in decibel; riportiamo per comodità l'algoritmo 8):

8)

scriviamo quindi la relazione che vogliamo tra le due funzioni:

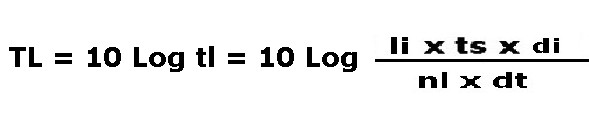13)

se svolgiamo il calcolo logaritmico della 13) otteniamo:

TL = 10 Log tl = LI + TS + DI - NL - DT = 10 Log [(li x ts x di) / (nl x dt)] =
= 10 Log (li) + 10 Log (ts) + 10 Log (di) - 10 Log (nl) - 10 Log (dt) =
= 10 Log ( 189.6 x 1021 ) + 10 Log (10) + 10 Log (294) - 10 Log (158.4 x 103) - 10 Log (735)=
= 232.8 dB + 10 dB + 24.7 dB - 52 dB - 28.7 dB = 186.8 dB





Home

Stampa immagine grafica o descrizione testuale