-unica soluzione condizionata secondo il teorema dei seni: precisione ad 1'' -
noti due lati e l'angolo adiacente

1)Un triangolo qualunque e i suoi elementi
In figura 1 è tracciato un triangolo qualunque con tutti i suoi elementi, distinti da lettere ed angoli, ai quali faremo riferimento nel prosieguo del lavoro.

figura 1

2)Premesse
Per la soluzione dei triangoli qualunque, in particolare avendo come elementi noti due lati: a ; b ed un angolo adiacente: alfa, è necessario che siano verificate alcune condizioni:
che sia:
1) b Sen ( alfa ) < = a
(se questa condizione non è verificata gli elementi dati non consentono la soluzione del triangolo.)

2) lato "b" < lato "a" ; questa condizione, assieme alla 1) verificata, consente un'unica soluzione del triangolo.

3) lato "b" > lato "a" ; e alfa < 90° ; questa condizione, assieme alla 1) verificata, consente due soluzioni del triangolo.

Nel triangolo di figura 1 si vede che il lato "b" < lato "a" quindi, verificata la 1, la soluzione unica è possibile è illustrata di seguito.

3)Il calcolatore
Il calcolatore è stato sviluppato come file eseguibile con il quale, in base alla prescelta terna di elementi, si computano rapidamente tutti gli altri con una precisione di 1'' ( un secondo in gradi sessagesimali ); naturalmente il calcolo è subordinato alle condizioni 1) e 2) del paragrafo precedente.
Il pannello operativo del calcolatore è mostrato in figura 2:

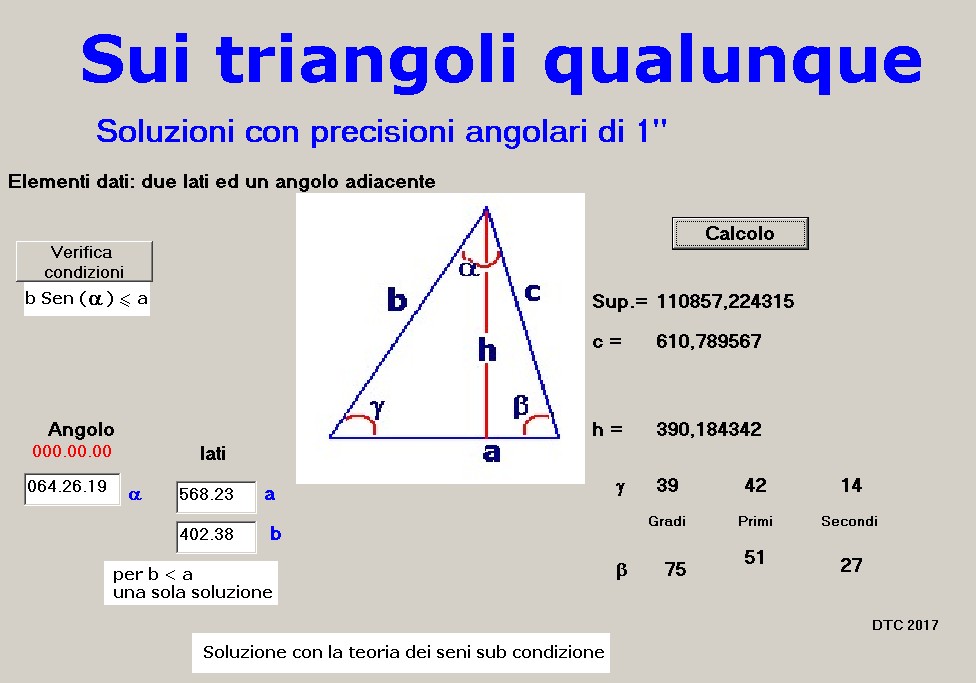figura 2

Il calcolo, come detto, è subordinato alla condizione: che sia: b Sen ( alfa ) < = a , condizione che se non verificata non consente al software di operare e quindi di dare risultati dando la sensazione che il calcolatore non funzioni; per eliminare ogni dubbio, dopo l'inserzione dei dati; i due lati e l'angolo, si preme il pulsante di verifica: se si colora in verde la condizione è verificata, altrimenti assume il colore rosso che indica l'impossibilitò di procedere ai calcoli.
Facendo riferimento alla figura 2 vediamo il caso in cui la terna di elementi noti sia:
a = 568.23
b= 402.38
alfa = 64° 26' 19''
ne segue che la condizione: b Sen ( alfa ) ≈ 363 < a è verificata .
Gli elementi del triangolo, calcolati secondo il teorema dei seni e la condizione citata, sono mostrati a destra dopo la pressione del pulsante "Calcolo"

4)Osservazioni
La soluzione del triangolo, essendo b < a, è unica; esiste quindi un solo triangolo con i tre elementi dati.
Si tenga presente che il programma del calcolatore opera soltanto se la condizione b < a è verificata.
In una prossima pagina prenderemo in esame il caso in cui sia b > a ; condizione che da luogo a due diverse soluzioni del triangolo.

5)Esercitazioni
Per sviluppare esercitazioni sul calcolatore cliccare sull'eseguibile Poligonali-4, quindi, in base alla tabella sotto riportata, scegliendo a piacere terne di lati, si possono fare numerosi esercizi per avere riscontri sull'impiego del calcolatore

Home

Stampa immagine grafica o descrizione testuale