-doppia soluzione condizionata secondo il teorema dei seni: precisione ad 1'' -
noti due lati e l'angolo adiacente

1)Un triangolo qualunque e i suoi elementi
Nella figura 1 è tracciato un triangolo qualunque distinto dai tre elementi, "a"; "b"; alfa: i cui valori sono riportati nella figura stessa.

figura 1

La soluzione di detto triangolo, avendo a < b e alfa < 90 ° ci riporta a quanto già dichiarato in p209 che riportiamo:

Per la soluzione dei triangoli qualunque, in particolare avendo come elementi noti due lati: a ; b ed un angolo adiacente: alfa, è necessario che siano verificate alcune condizioni:
che sia:
1: b Sen ( alfa ) < = a
(se questa condizione non è verificata gli elementi dati non consentono la soluzione del triangolo.)

2: lato "b" < lato "a" ; questa condizione, assieme alla 1) verificata, consente un'unica soluzione del triangolo.

3: lato "b" > lato "a" ; e alfa < 90° ; questa condizione, assieme alla 1) verificata, consente due soluzioni del triangolo.

Siamo quindi nella condizione 3) che andremo a risolvere in due passi distinti:

A- Soluzione del triangolo di figura 1 con il calcolatore già impiegato in p209 .
B- Trasformazione del triangolo di figura 1 in uno diverso avente però la stessa terna di elementi del primo e soluzione con il calcolatore già impiegato in p205.

2)Passo A-: Soluzione del triangolo di figura 1
Con il calcolatore già utilizzato in p209 che riportiamo: Poligonali-4, inserendo gli elementi noti di figura 1, a = 316.24; b = 412.63; alfa = 41° 36' 53'' otteniamo il pannello di lavoro con gli elementi risolutivi del triangolo dato:

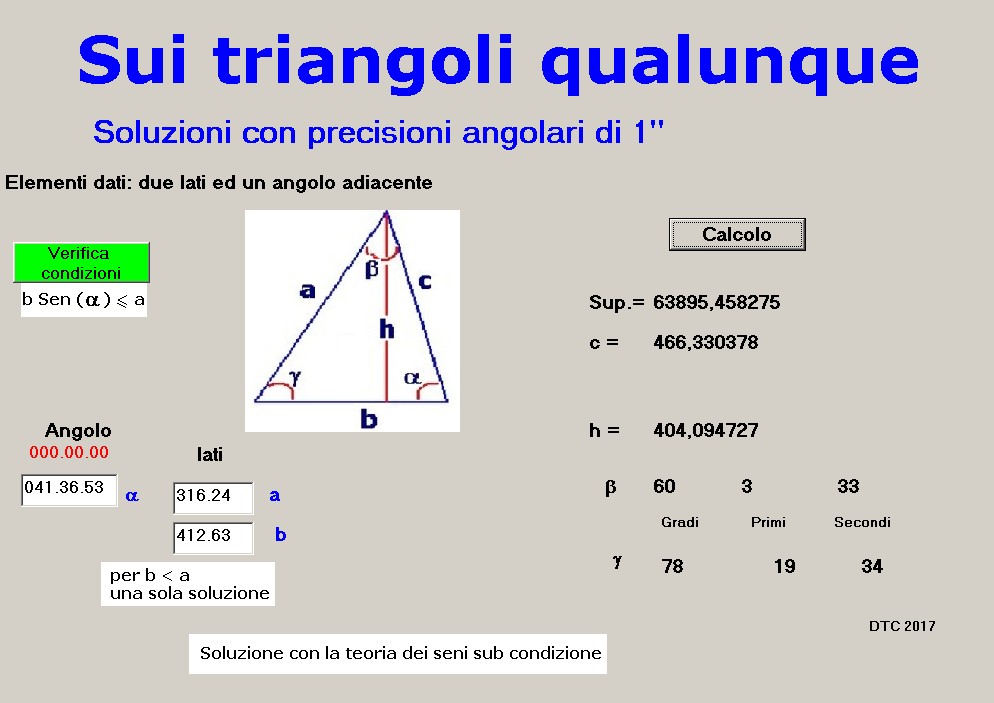figura 2

Tutti gli elementi del triangolo dato utili per il calcolo secondo il passo B) sono riportati in figura 3:

figura 3

3)Passo B-: Costruzione del triangolo relativo alla seconda soluzione del triangolo di figura 1
La costruzione del secondo triangolo si basa sulla rotazione del lato "a" verso "b" così come mostrano le figure 4/I e 4/II:

figure 4

Si tratta quindi di risolvere un triangolo avente noti i due lati è l'angolo compreso:
Dalla nuova geometria del triangolo, figura 4/II, e dai valori riportati in figura 3, si evince:

a = 316.24
b = 412.63;
gamma* = beta - alfa = 60° 3' 33'' - 41° 36' 53'' = 18° 26' 40''

Per la soluzione di questo triangolo si ricorre al calcolatore utilizzato in p205 che riportiamo Poligonali-2, la soluzione del nuovo triangolo è riportata in figura 5:

figura 5

4)Esercitazioni
Per sviluppare esercitazioni sul metodo di calcolo cercare nella tabella sotto riportata le terne di elementi utili per il complesso sistema di soluzione.

Home

Stampa immagine grafica o descrizione testuale