1) Introduzione

Le curve caratteristiche che individuano un trasduttore piezoelettrico, visto dal lato dell'inserzione energia elettrica, sono relative all'andamento della sua impedenza Zi o ammettenza Yi in funzione della frequenza.
In questa pagina prenderemo in esame le caratteristiche d'impedenza che si concretizzano attraverso due diagrammi:
La curva della variazione del modulo dell'impedenza Zi indicato con |Zi|.
Il cerchio d'impedenza relativo alle componenti ortogonali del modulo |Zi|.
I due diagrammi sono tracciabili, in via teorica, una volta noti i parametri fisici del trasduttore quali:
Capacità mozionale Cm.
Induttanza mozionale Lm.
Resistenza mozionale Rm.
Capacità bloccata. Co
Naturalmente, una volta tracciati i diagrammi, resta la verifica sperimentale in acqua così come previsto dai piani costruttivi del trasduttore piezoelettrico; detta verifica mostrerà il reale cerchio d'impedenza che non dovrà scostarsi troppo dal cerchio teorico.

2) Il circuito equivalente di un trasduttore piezoelettrico

Il circuito equivalente di un trasduttore piezoelettrico in acqua è riportato in figura 1:



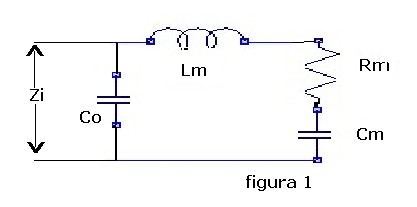
In essa si possono osservare i diversi parametri caratteristici del dispositivo dipendenti, sia dalla struttura puramente elettrica, sia da quella meccanica:
Per la parte elettrica - Co è la capacità bloccata del trasduttore.
Per la parte meccanica - Cm, Lm, Rm, sono rispettivamente:
Cm - l'equivalente elettrico della rigidità meccanica
Lm - l'equivalente elettrico della massa meccanica
Rm - l'equivalente elettrico della resistenza meccanica interna e di radiazione
I quattro parametri caratterizzano la frequenza Fm di risonanza in acqua del trasduttore e la sua impedenza d'ingresso Zi.
In base alla figura 1 ed ai valori dei parametri si tracceranno, come vedremo, le curve caratteristiche del trasduttore.

3)Studio della funzione caratteristica Zi

Per semplificare la redazione delle diverse espressioni che concorrono al calcolo della funzione Zi si adottano i seguenti simboli ridotti:

c in vece di Cm ( in Farad ).
l in vece di Lm ( in Henry).
r in vece di Rm ( in Ohm ).
co invece di Co ( in Farad ).
Si pone p = 3.1415927.
Con f la frequenza ( in Hz ).
Con * in vece di x s'indica il prodotto.
Con ^ s'indica l'elevamento a potenza
Si pone w = 2 p f al posto di ω = 2 p f

Nella figura 2 possiamo osservare come la Zi dipenda dal parallelo tra i due rami, in celeste quello relativo all'impedenza Zb dovuta alla capacità bloccata Co, e quello in rosso relativo all'impedenza Zm dovuta alla serie delle tre componenti mozionali:



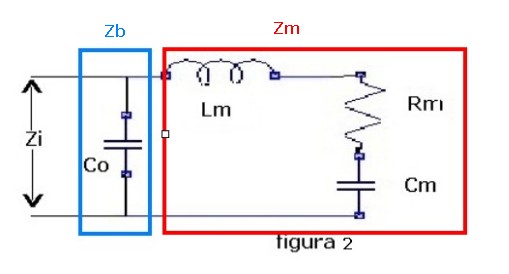
Sarà quindi Zi = Zb // Zm ; ( il simbolo // indica il parallelo tra le due impedenze )
L'espressione di Zb in termini complessi é:
Zb = - J / (w * co)
L'espressione di Zm in termini complessi è:
Zm = J(w * l) - (J / (w * c)) + r = J[(w * l) - (1/(w * c))] + r

Il parallelo tra Zb e Zm è:

[- J / (w * co)] * [J[(w * l) - (1/(w * c))] + r]
_______________________________________
[- J / (w * co)] + [J[(w * l) - (1/(w * c))] + r]

ovvero:

(w * l - 1 / w * c) * (1 / w * co) - j (r / w * co)
______________________________________
j[(w * l - 1 / w * c) - 1 / w * co] + r

ponendo:
a = (w * l - 1 / w * c)
b = (1 / w * co)
l'espressione di Zi diventa graficamente più semplice e manipolabile:

a * b - J r * b
_____________
J( a - b ) + r

La Zi così espressa, dopo operazioni ordinarie sui numeri complessi, si presenta con le due componenti reale ed immaginaria come segue:

Parte reale: Re = (((a * b * r) - ((r * b) * (a - b)))) / [ r ^ 2 + ((a - b) ^ 2)]

Parte immaginaria: Imm = J [(-(a * b) * (a - b) - (r ^ 2 * (b)))/ [ r ^ 2 + ((a - b) ^ 2)]]

A questo punto non resta che implementare in una routine di calcolo su P.C. le due parti per ottenere il risultato voluto.

4)Come si presentano i grafici del modulo e del cerchio d'impedenza

Per quanto visto al paragrafo precedente possiamo scrivere:
Zi = Re + J Imm , ed il modulo di Zi, indicato con |Zi| sarà:
|Zi| = √ ( Re^2 + Imm^2); questa è l'impedenza d'ingresso del trasduttore il cui andamento sarà simile al grafico di figura 3 dove sono evidenziate la frequenza di risonanza fr e antirisonanza fa:



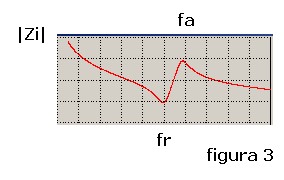
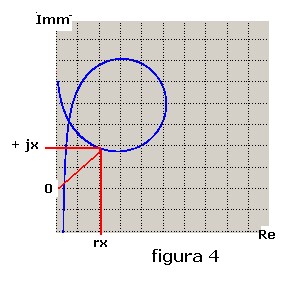
Per il cerchio d'impedenza si tratta di utilizzare le componenti cartesiane del modulo,
Re = rx ed Imm = jx, come coordinate dei punti estremi che tracciano il cerchio così come mostrato in figura 4:

5)Esempio di calcolo in Visual Basic

Con una routine di calcolo e grafica in Visual Basic (qualsiasi altro programma di elaborazione può essere impiegato) si mostra un esempio relativo alle caratteristiche di un trasduttore piezoelettrico basato su di una serie di parametri implementati a programma per l'esercizio da svolgere, questi sono:

Co = co = 1500 / 1000000000000# Farad
Cm = c = 500 / 1000000000000# Farad
Lm = l = 0.5 Henry
Rm = r = 3200 Ohm

Calcolo e grafico del modulo:
In figura 5 è mostrato, in rosso, il grafico del modulo |Zi| che, in funzione di una variazione di frequenza compresa tra 1000 Hz e 20000 Hz, mostra il suo minimo in corrispondenza di fr ≈ 10000 Hz (frequenza di risonanza); minimo pari al valore di "r ≈ 3200 ohm" .

figura 5

Questa curva si ottiene dopo aver pigiato il pulsante "Calcolo" indipendentemente dai comandi e dati vicini ad esso necessari invece per il calcolo e il grafico del cerchio d'impedenza.

Calcolo e grafico del cerchio d'impedenza:
In figura 6 è mostrato, in blu, il grafico del cerchio d'impedenza , in funzione di una variazione di frequenza compresa tra 1000 Hz e 20000 Hz.
Sul cerchio si sono volute determinare, a titolo d'esempio, le componenti ortogonali ( Rx, Jx ) calcolate alla frequenza di 11720 Hz impostata con il VScrool.
Come si vede dai label a destra per f = 11720 Hz abbiamo sul cerchio R = 24723.93 Ohm ; jx = -13740.5 evidenziati con un dischetto rosso sopra il cerchio d'impedenza.
Il risultato illustrato è stato ottenuto, dopo aver impostato il valore di frequenza, dopo la pressione del pulsante "Calcolo"
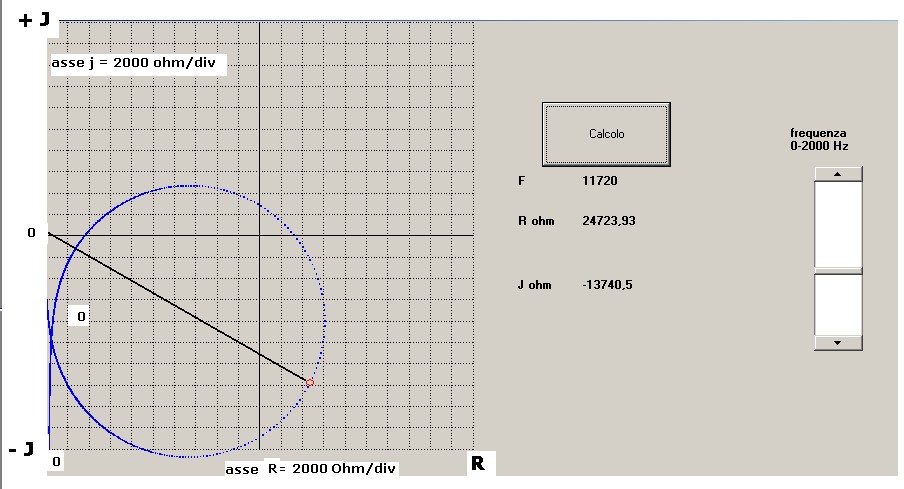. figura 6

6)Il programma di calcolo in Visual Basic

Per dare un'idea delle routine di calcolo e presentazione grafica utilizzate per i diagrammi dei quali abbiamo trattato viene qui esposto un listato di istruzioni in Visual Basic con annessi commenti.
Come si vedrà i parametri del trasduttore sono implementati in routine, nulla vieta di aggiungere nuove routine per l'inserzione dei dati da pannello.
I grafici di |Zi| e del cerchio d'impedenza possono essere tracciati contemporaneamente o in fasi separate bloccando o no le istruzioni indicate al punto """"" del programma.


LISTATO DEL PROGRAMMA
Dim w As Double ' Dichiarazioni delle variabili
Dim co As Double
Dim c As Double
Dim a As Double
Dim b As Double
Dim k As Double
Dim k1 As Double
Dim k2 As Double
Dim modulo As Double
Dim mem(10)

Private Sub Command1_Click() ' Routine comandata dal pulsante "Calcolo"
Cls

'Istruzioni per la grafica del reticolo cartesiano
For x = 0 To 6400 Step 320
For y = 0 To 6400 Step 40
PSet (x, y), 7
Next y
Next x
For y = 0 To 6400 Step 320
For x = 0 To 6400 Step 42
PSet (x, y), 7
Next x
Next y
Line (3200, 0)-(3200, 6400)
Line (0, 3200)-(6400, 3200)

For f = 1000 To 20000 Step 10 ' Anello di calcolo

'Inserzione parametri trasduttore
p = 3.14159
w = 2 * p * f
co = 1500 / 1000000000000#
c = 500 / 1000000000000#
l = 0.5
r = 3200

'Sostituzioni per semplificare le impostazioni delle istruzioni (da paragr. 3)
a = (w * l) - (1 / (w * c))
b = 1 / (w * co)
k = r ^ 2 + ((a - b) ^ 2)

'Implementazione formule di calcolo come da paragrafo 3)
k1 = (((a * b * r) - ((r * b) * (a - b)))) / k
k2 = (-(a * b) * (a - b) - (r ^ 2 * (b))) / k
modulo = Sqr((k1 ^ 2) + (k2 ^ 2))

'Istruzioni per evidenziare estremo modulo sul cerchio
If f = mem(5) Then colore = vbRed Else colore = vbBlue
If f = mem(5) Then dia = 50 Else dia = 5

Istruzioni per porre in memoria coordinate cartesiane del modulo
If f = mem(5) Then mem(1) = k1
If f = mem(5) Then mem(2) = k2
If f = mem(5) Then Label6.Caption = f

'""""" Istruzione per la grafica del modulo |zi|
PSet ((3200 / 20000) * f, 3200 - (3200 / 10000) * modulo / 2), vbRed

'""""" Istruzione per la grafica del cerchio
If k2 < -22000 Then k2 = -22000
Circle ((3200 / 20000) * k1, 3200 - (3200 / 20000) * k2), dia, colore

Next ' Ripetizione anello di calcolo

'Istruzioni per la visualizzazione dei valori Rx: jx e f
Label1.Caption = Format((mem(1)), "0.##")
Label2.Caption = Format((mem(2)), "0.##")
Label6.Caption = mem(5)
End Sub ' fine anello di calcolo

'Routine per l'inserzione del valore di frequenza dal VScroll
Private Sub VScroll1_Change()
Label1.Caption = ""
Label2.Caption = ""
mem(5) = Int(VScroll1.Value / 10) * 10
Label6.Caption = mem(5)
End Sub











Home

Stampa immagine grafica o descrizione testuale

==============================