SONAR-INFO-p230
ESERCOMPLEX
-Esercizi di calcolo sui numeri complessi-
Gli esercizi di calcolo sui numeri complessi sono più intuitivi se accompagnati da presentazioni grafiche dinamiche che si adattino, di volta in volta, ai valori dei numeri complessi da elaborare ed al risultato dell'elaborazione.
Per ottemperare a tale esigenza è proposto in questa pagina un file eseguibile che consente di svolgere rapidamente le quattro operazioni base sui numeri complessi coaudiuvato dal
contemporaneo tracciamento in assi cartesiani nella loro forma vettoriale.
I numeri complessi da mettere a calcolo sono soltanto due, ma con operazioni successive si possono sviluppare, come vedremo, qualsiasi tipo di computazione.
2) Il pannello di calcolo di ESERCOMPLEX
Una volta lanciato l'eseguibile Complex si visualizza sul P.C. la schermata di figura 1 che andiamo a commentare:
figura 1 (Pannello operativo)In alto a sinistra è posizionato il reticolo cartesiano per la presentazione grafica dei numeri complessi definiti con l'espressione: N = R , j x
Il valore delle scale in ascisse e ordinate è, al ancio, di 1/div. pari quindi a +/- 10 unità sulle due coordinate R e j.
Il dato di scala può essere modificato a piacere digitando sul TextBox (fondo scala), collocato in basso a destra, il valore voluto.
Nei quattro TextBox a destra, individuati dalle scritte R j e:
V1 (colore rosso)
V2 (colore blu)
si devono digitare rispettivamente le parti reali (R) ed immaginatie (j) dei due numeri complessi da elaborare.
I 5 pulsanti in alto a destra, nella sequenza:
"I singoli vettori"
"Somma"
"Differenza"
"Prodotto"
"Divisione"
Hanno il compito, il primo di visualizzare i vettori impostati, gli altri quattro per eseguire le operazioni su di essi indicate.
I risultati delle quattro operazione sono indicati, per ciascun pulsante, a destra in due diverse tipologie:
-in coordiane cartesiane: parte reale R , parte immaginaria jx
-in coordinate polari: modulo M e argomento Arg° in gradi sessagesimali
3) Esempi di presentazione e calcolo
Una volta digitati i valori dei numeri complessi da elaborare se ne può vedere la grafica a colori nel reticolo cartesiano a seguito della pessione del tasto " I singoli vettori", questa operazione consente, volendo, il cambio di scala più adatto alla presentazione che si desidera.
Un esempio per i vettori:
V1 = +4.5 , -j 7
V2 = +3.2, +j 2.8
è riportato in figura 2:
figura 2 ( grafico vettori inseriti a calcolo)Volendo, ferme restando le impostazioni dei numeri precedenti, si possono premere in sequenza i quattro pulsanti di calcolo ottenendo la grafica ed i valori risolutivi delle operazioni eseguite così come mostra la figura 3 dove il grafico è relativo all'ultima operazione, la "Divisione", dove il vettore risultante è di colore verde.
A fianco di cascun pulsante sono indicati i risultati, in forma cartesiana e polare, relativi al tipo di calcolo espresso dal pulsante stesso.
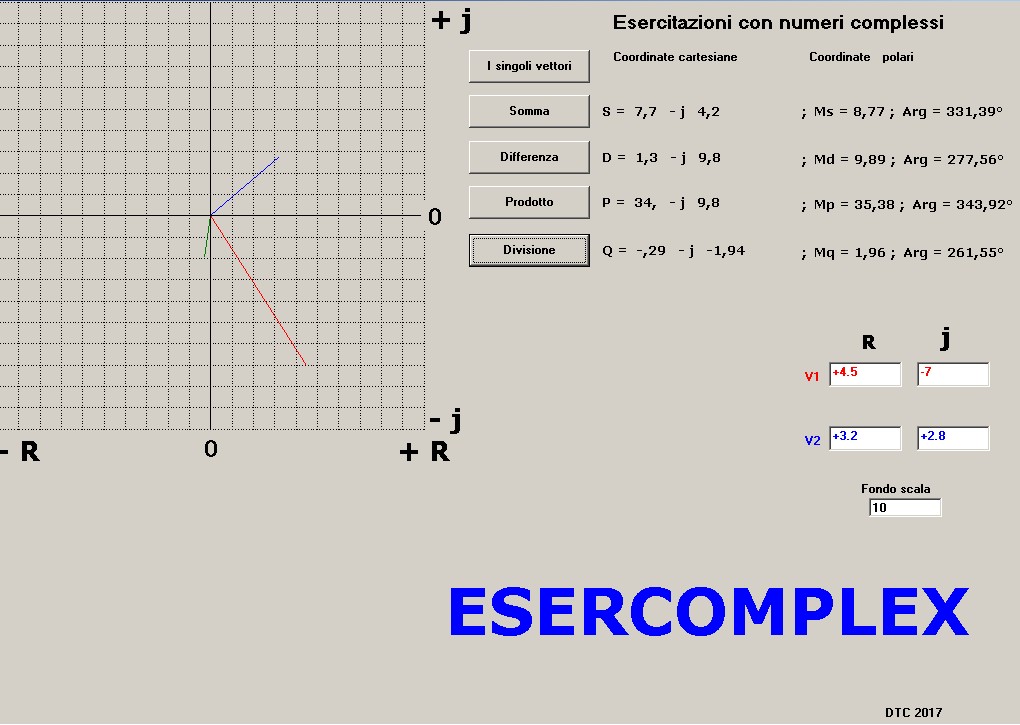figura 3 (Sequenza delle quattro operazioni)Per vedere l'uno dopo l'altro i grafici relativi alle quattro operazioni, fermi restando i dati d'ingresso, si preme il tasto "I vettori" e di seguito il tasto dell'operazione che vogliamo eseguire.
Riportiamo ora le immagini che mettono in evidenza soltanto il pulsante dei cinque del quale voggliamo sia i risultati del calcolo che i grafici conseguenti; queste sono nell'ordine:
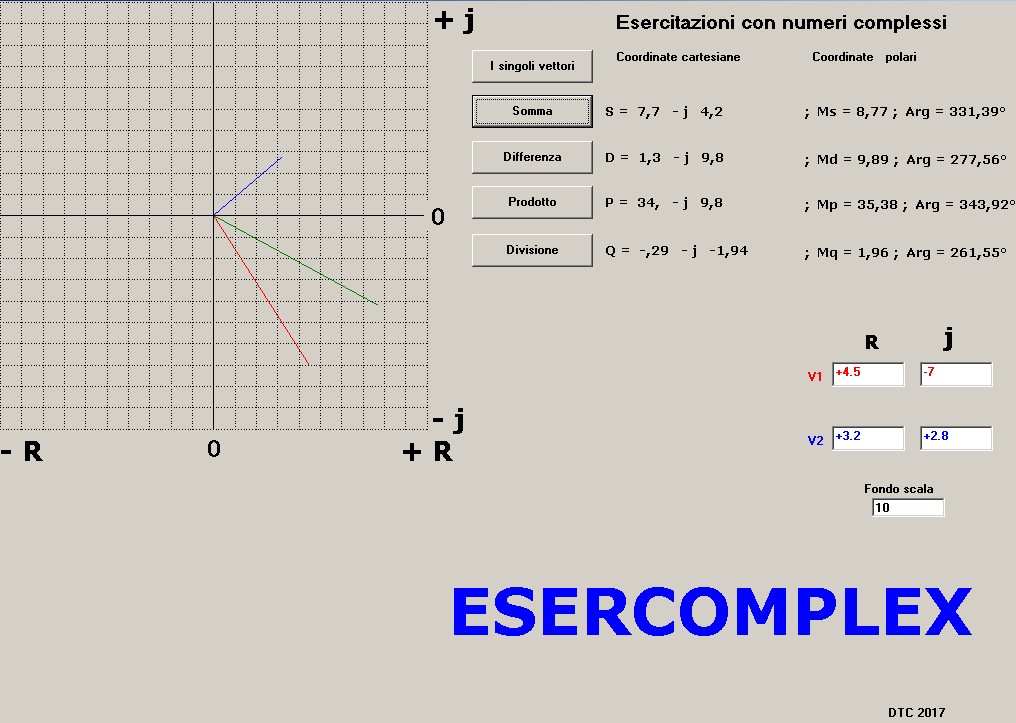figura 4 (Somma)
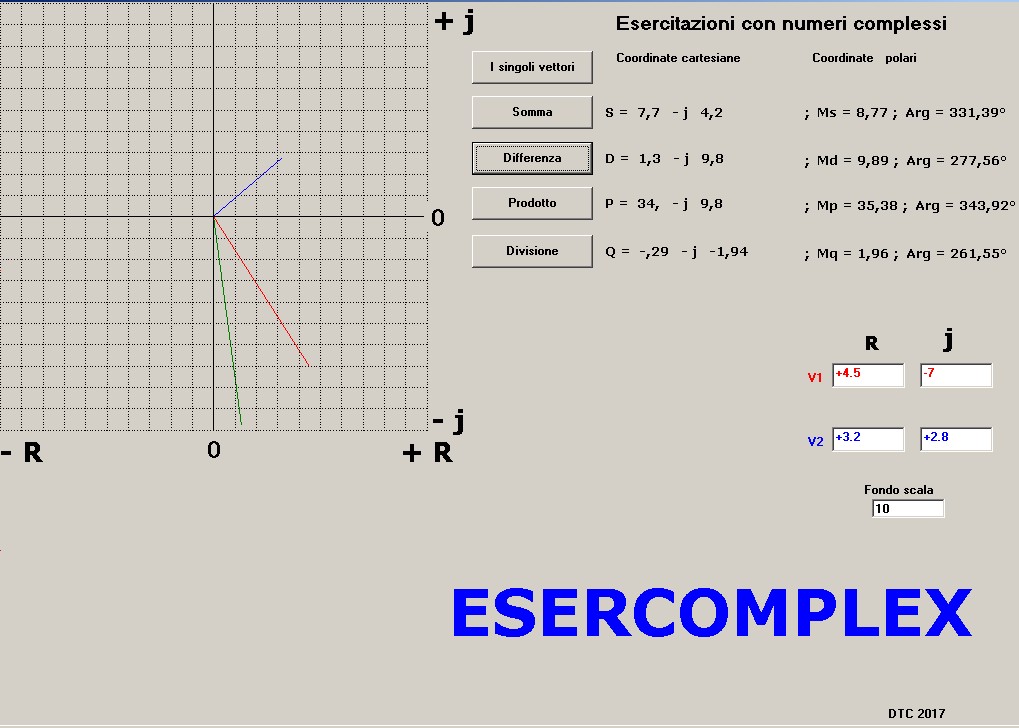figura 5 (Differenza)
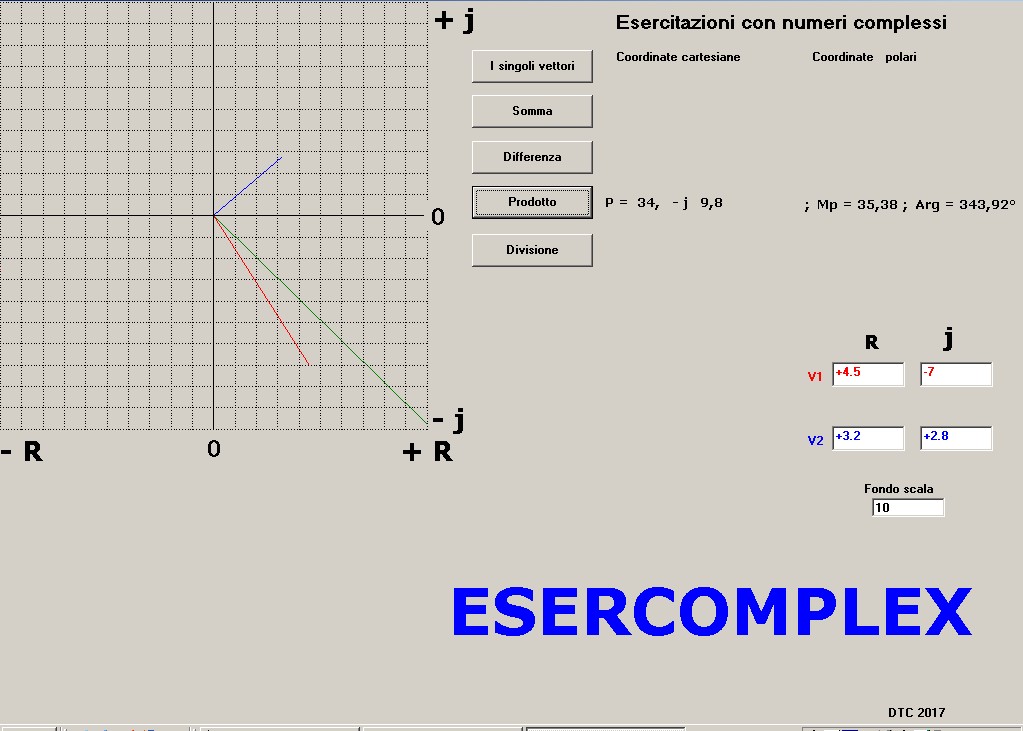figura 6 (Prodotto)figura 7 (Divisione)4) Aggiustaggio fondo scala
Si può ricorre all'aggiustaggio del fondo scala qualora l'entità dei valori dei numeri complessi da inserire sia superiore a 10 unità.
Se ad esempio:
v1 = + 345.65 , -j 442.6
v2= +54 , j63.4
si cambierà il fondo scala da 10 a 500 ottenendo il seguente risultato grafico:
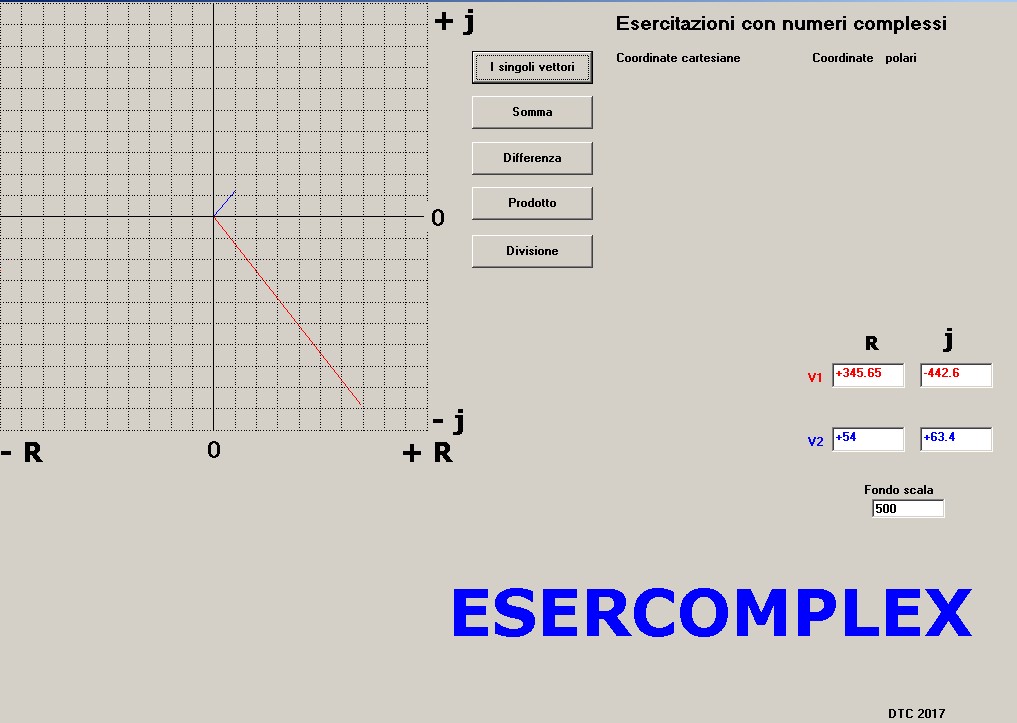figura 8 (Cambiamento fondo scala)5) Calcoli multipli
Sia da sviluppare la seguente espressione con termini complessi:
N = [(va + vb) x (vc/vd)] / va
posto .
Y1 = (va + vb)
Y2 = (vc/vd)
Y3 = Y1 x Y2
N = Y3 / va
si scinde l'espressione in blocchi da due termini ciascuno, ad esempio:
y1 = (va + vb)
si calcola la somma Y1 con l'eseguibile e si prende nota carta e matita
y2 = (vc/vd) si calcola la divisione Y2 e si prende nota
si calcola con Y3 il prodotto di Y1 con Y2 e si prende nota
infine si esegue la divisione tra Y3 e va
6) Trasformazione di un numero complesso da cartesiano in polare
La trasformazione di un numero complesso, espresso nella forma cartesiana ( R, jx ), in coordinate polari ( M, Arg° ) è immediata; basta digitare ( R, jx ) in V1 e premere "somma".