SONAR-INFO-p231
Calcolatore della DFT
Discrete Fourier Transform
1) Generalità 2) Per il computo della DFT: le variabili da inserire a calcolo 3) Esempio d'impostazione delle variabili di cui al paragrafo 2) 4) Il pannello operativo del calcolatore DFT 5)Primo esempio di calcolo DFT con controllo analitico 6)Secondo esempio di calcolo DFT con controllo analitico 7)Esempio di calcolo DFT senza controllo analitico 8)Esempio di calcolo DFT per impulso di segnale sinusoidale
 figura 1
figura 1
consente, per via esclusivamente matematica, l'analisi dei fenomeni transitori di legge nota, F(t), funzioni
del tempo, quali ad esempio l'impulso di sinusoidi di figura 2.
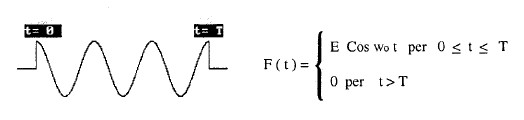 figura 2
figura 2
mediante la determimazione del loro spettro di frequenza G ( w ) mostrato in figura 3.
 figura 3
figura 3
Se dell'impulso da analizzare non si conosce la legge F(t), come ad esempio per l'impulso casuale
mostrato in figura 4:
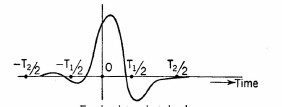 figura 4
figura 4
la trasformata di fourier non è applicabile; è sostituibile, con buona approssimazione,
dall'algoritmo DFT ( Discrete Fourier Transform ) che computa il modulo dello spettro, secondo l'espressione di figura 5.
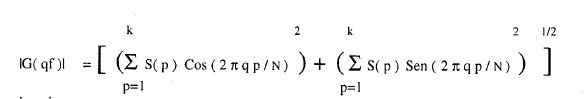 figura 5
figura 5
Per un numero finito di campioni prelevati dall'impulso, mostrati in rosso in figura 6a:
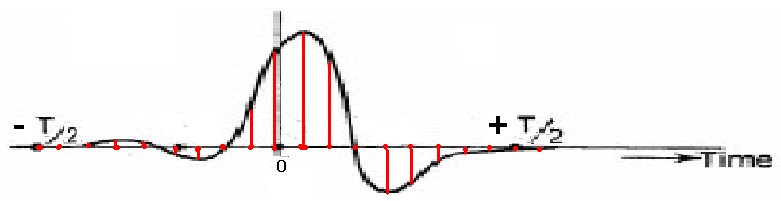 figura 6a
figura 6a
la DFT computa un numero finito di valori del modulo della G(w) così come riportato in figura 6b:
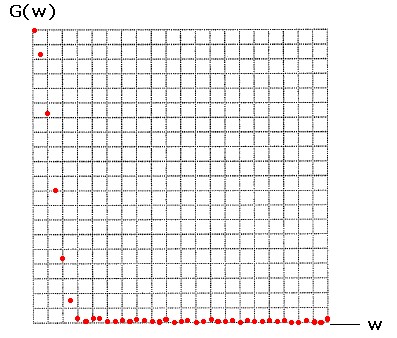 figura 6b
figura 6b
Ragione di questa pagina è l'illustrazione di un caratteristico file di calcolo in grado di computare e tracciare
il modulo dello spettro di un impulso qualsiasi secondo l'algoritmo della DFT.
Maggiori chiarimenti sulla DFT sono disponibili sull'estratto dal testo di pagina p11 al seguente capitolo
in pdf:
Capitolo 8

figura 7
 figura 8
figura 8
Le caratteristiche temporali dell'impulso siano: T/2 = 0.005 Sec. quindi T = 0.01 Sec.
Si voglia il campo di frequenza d'analisi compreso tra 0 e 1000 Hz: quindi Fmax = 1000
Si voglia una definizione d'analisi in frequenza a passi di 25 Hz, quindi DF = 25 Hz
In base ai dati esposti si calcolano:
Il numero dei campioni da prelevare dall'impulso: k = 2 T Fmax = 2 * 0.01 Sec. * 1000 Hz = 20
Il valore di N: N = 2 Fmax/DF = 2 * 1000 / 25 = 80
Il numero dei campioni che rappresenteranno il modulo dello spettro: q = Fmax/DF = 1000/25 = 40
Da rilievi su figura 8 si annotano le ampiezze dei k valori dei campioni dell'impulso, da p1 a p20, evidenziati con righe rosse;
questi saranno inseriti a calcolo l'uno dopo l'altro.
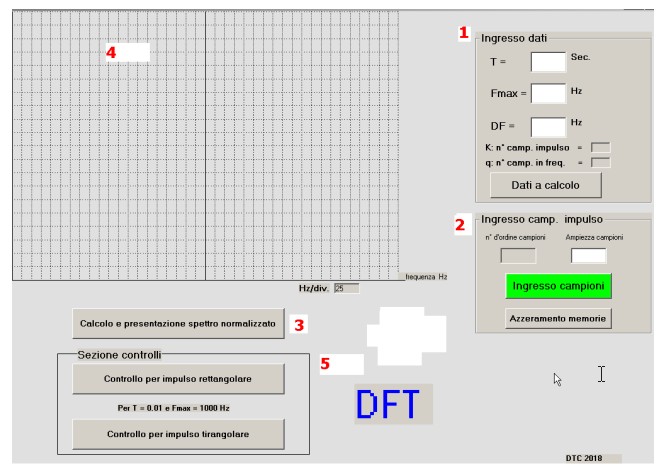 figura 9
figura 9
Sezione 1 (ingresso dati) :
La sezione contiene 3 textbox nei quali inserire, l'una dopo l'altra, le seguenti variabili:
Durata dell'impulso da analizzare espressa con T (Sec.)
Estremo della frequenza d'analisi espressa con Fmax (Hz)
Intervallo voluto tra due campioni dello spettro con DF (Hz)
Pulsante " Dati a calcolo" per l'avvio delle computazioni indicate nel paragrafo 3)
Due label per l'indicazione dei valori calcolati:
k ( numero dei campioni da ricavare dall'impulso)
q ( numero dei campioni che definiranno il modulo dello spettro di frequenza)
Al lancio del programma sono predisposti, in via provvisoria, i seguenti dati: T = 0.01 Sec; Fmax = 1000 Hz; DF = 1 Hz
Sezione 2: (ingresso campioni impulso)
La sezione contiene un label, a sinistra, che indica il numero progressivo dei campioni dell'impulso da analizzare
e un textbox, a destra, per l'inserzione delle ampiezze dei diversi campioni dell'impulso.
Un pulsante "Ingresso campioni" per l'inserzione progressiva dei valori sopra citati ed un
pulsante " Azzeramento memorie" per la ripetizione, se necessario, dell'inserzione dati.
Sezione 3: ( presentazione spettro)
La sezione contiene il pulsante "Calcolo e presentazione spettro normalizzato " per l'avvio del programma di
calcolo e presentazione grafica del modulo della DFT.
Sezione 4: ( reticolo cartesiano per il tracciamento del modulo dello spettro)
In ascisse, la frequenza d'analisi Fmax divisa in 40 intervalli, con label indicativo dell'entità di ciascun intervallo
in Hz/Div.
In ordinate l'ampiezza dello spettro, in forma normalizzata in 20 intervalli da 0.05/Div.
Il grafico dello spettro, rappresentando l'ampiezza del modulo, sarà sempre positivo
Sezione 5: (funzioni di controllo))
Con due pulsanti distinti è possibile tracciare il modulo dello spettro di due impulsi caratteristici:
Impulso rettangolare (ottenuto da calcolo per via analitica)
Impulso triangolare (ottenuto da calcolo per via analitica)
Questa sezione è utile per prendere confidenza, come vedremo, con il sistema di calcolo.
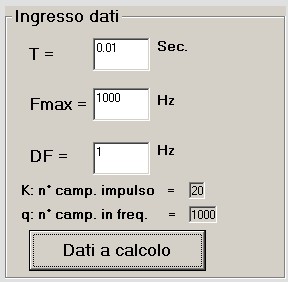 figura 10
figura 10
per : T = 0.01 Sec. - Fmax = 1000 Hz - DF = 1 Hz,
dopo la pressione del pulsante "dati di calcolo", si ha : k = 20 ; q = 1000 ;
dal calcolo emerge che sono necessari K = 20 campioni dell'impulso
Quindi: ampiezza E = 1, durata T = 0.01 Sec., k = 20.
I campioni dell'impulso, tutti uguali ad 1, sono inseriti in sezione 2 digitando nel textbox il primo di ampiezza 1
e di seguito, lasciando tale valore inalterato, premendo il pulsante "ingresso campioni" , s'inseriscono tutti
gli altri 19 fino a quando il pulsante citato diventa rosso; vedi figura 11
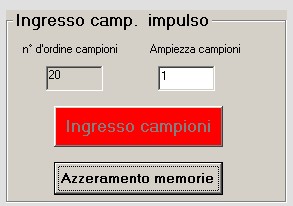 figura 11
figura 11
Con la successiva pressione del pulsante di sezione 3, si ha la presentazione del modulo dello spettro come riportato in
figura 12 con traccia in color viola:
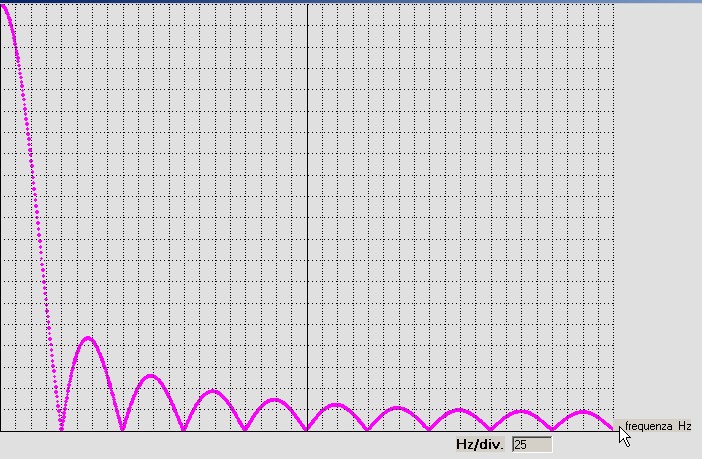 figura 12
figura 12
Per controllare la correttezza del processo DFT che ha portato allo spettro di figura 12 si può agire sulla
sezione 5; pulsante " Controllo per impulso rettangolare" che consente, per la via puramente analitica mostrata
in figura 13,
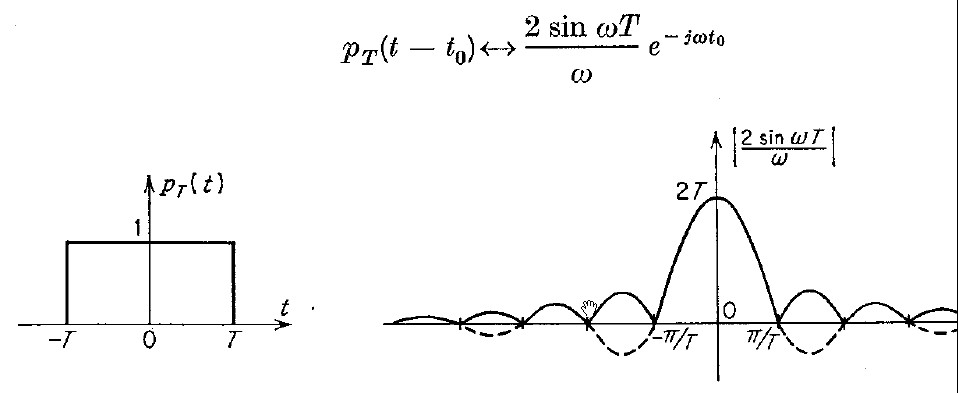 figura 13
figura 13
il tracciamento di una nuova curva di colore verde che, se il processo DFT svolto sarà corretto, si dovrà
sovrapporre, con buona approssimazione,
alla curva viola così come mostra figura 15:
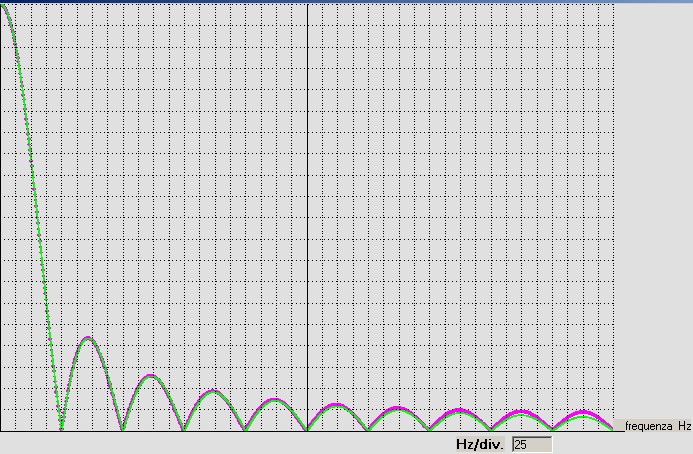 figura 15
figura 15
 figura 10
figura 10
per : T = 0.01 Sec. - Fmax = 1000 Hz - DF = 1 Hz,
dopo la pressione del pulsante "dati di calcolo", si ha : k = 20 ; q = 1000 .
L'impulso triangolare che vogliamo analizzare, della durata T = 0.01 sec. ha un profilo definito dalla seguente
sequenza di 20 valori:
0.1; 0.2; 0.3; 0.4; 0.5; 0.6; 0.7; 0.8; 0.9; 1; 0.9; 0.8; 0.7; 0.6; 0.5; 0.4; 0.3; 0.2; 0.1; 0
i campioni sono inseriti in sezione 2 digitando nel textbox il primo di ampiezza 0.1 ed in successione tutta
la sequenza sopra scritta premendo il pulsante "ingresso campioni" fino a quando il pulsante citato diventa rosso.
Con la successiva pressione del pulsante di sezione 3, si ha la presentazione del modulo dello spettro come
riportato in figura 16 con traccia in color viola:
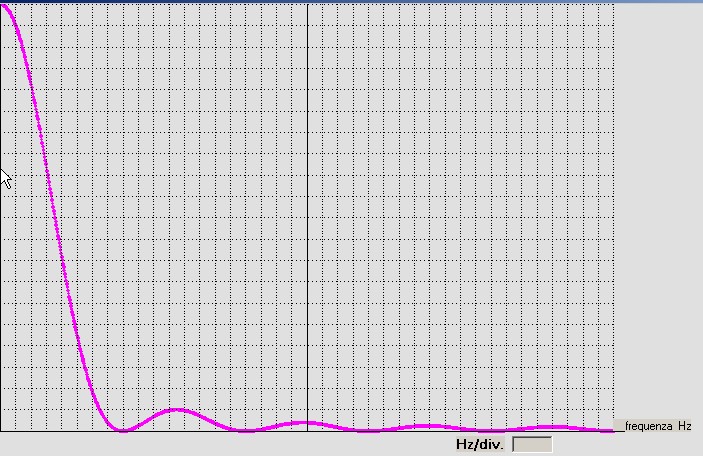 figura 16
figura 16
Per controllare la correttezza del processo DFT che ha portato allo spettro di figura 16 si può agire sulla
sezione 5; pulsante " Controllo per impulso triangolare" che consente, per la via puramente analitica mostrata
in figura 17,
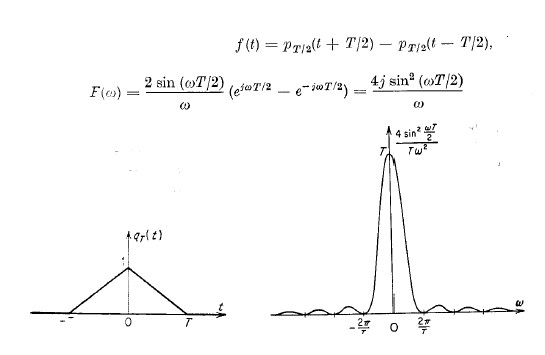 figura 17
figura 17
il tracciamento di una nuova curva di colore verde che, se il processo DFT svolto sarà corretto, si dovrà sovrapporre
alla curva viola così come mostra figura 18:
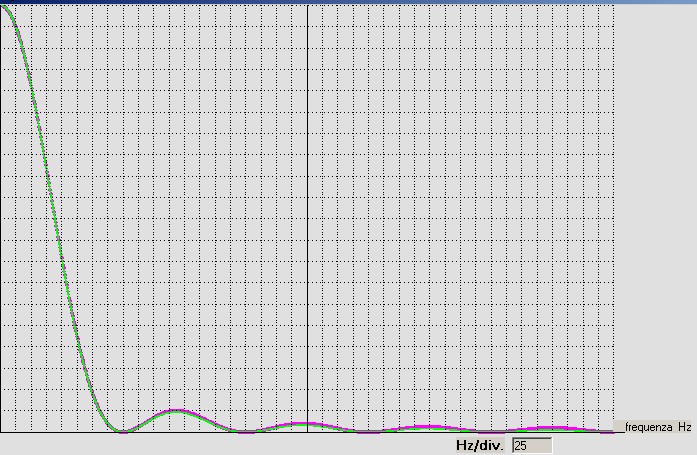 figura 18
figura 18
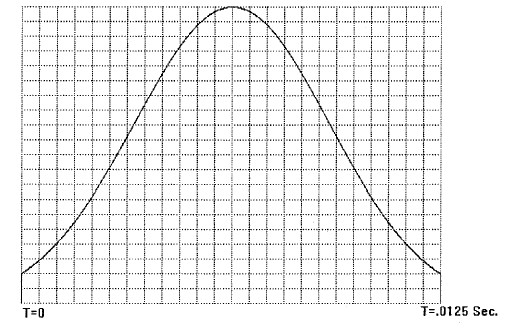 figura 19
figura 19
I dati relativi all'impulso siano:
Durata: T = 0.0125 Sec.
Ampiezza massima: E = 1
Massima frequenza voluta nella DFT: Fmax = 1000 Hz
Intervallo tra i campioni dello spettro: DF = 2 Hz
I valori calcolati nella sezione 1 sono riportati in figura 20:
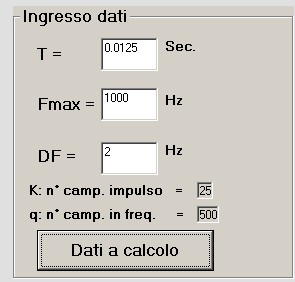 figura 20
figura 20
Dal calcolo emerge che sono necessari K = 25 campioni dell'impulso; questi, ricavati da figura 19 sono mostrati
in figura 21:
 figura 21
figura 21
Questi valori, messi a calcolo nella sezione 2, portano al modulo dello spettro di figura 22:
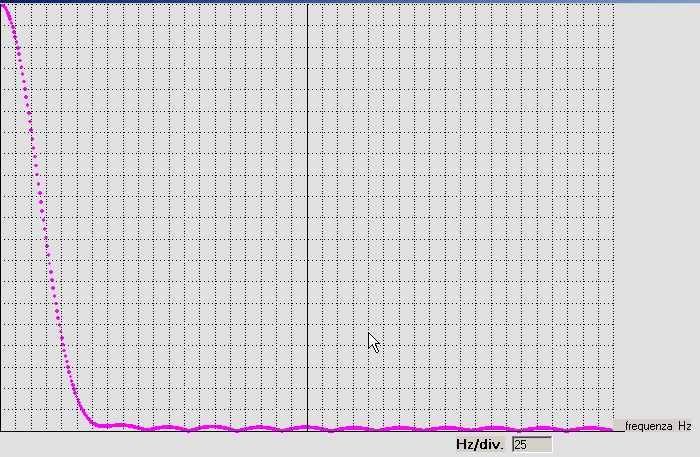 figura 22
figura 22
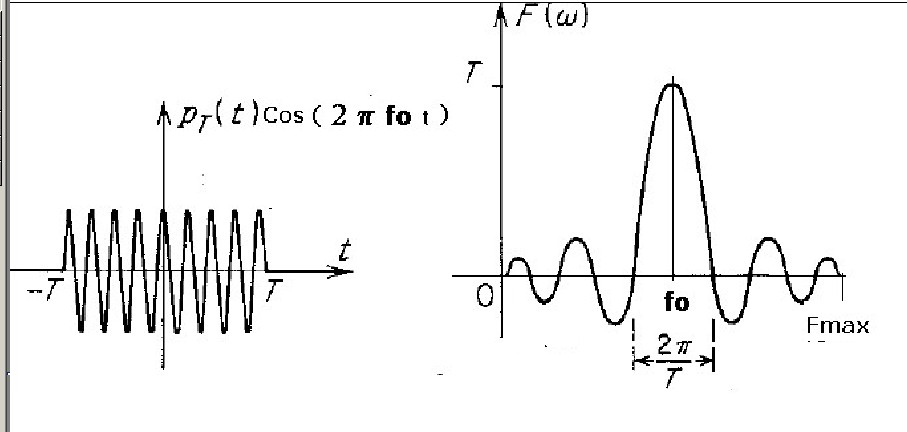 figura 22
figura 22
il processo di calcolo della DFT è simile a quelli in precedenza illustrati salvo il fatto che la massima ampiezza
dello spettro non sarà per f = 0 ma per f = fo come mostra figura 22.
Consideriamo ora un impulso del tipo riportato in figura 22 che abbia le seguenti caratteristiche:
Durata: T = 0.01 Sec.
Frequenza all'interno dell'impulso: fo = 400 Hz
Frequenza massima dello spettro voluto: Fmax = 1000 Hz
Intervallo tra i campioni dello spettro: DF = 2 Hz
Nella sezione 1, per T = 0.01 Sec, Fmax = 1000 Hz, DF = 2 Hz, si ha K = 20:
I 20 campioni richiesti si ottengono dalla funzione:
Y = A Cos(6.28 * fo * t) dove A = 1, fo = 400 Hz, t = 0.5 mSec/campione
così come mostra la tabella di figura 23:
 figura 23
figura 23
Lo spettro dell'impulso, calcolato tra F = 0 e Fmax = 1000 Hz si presenta come in figura 25:
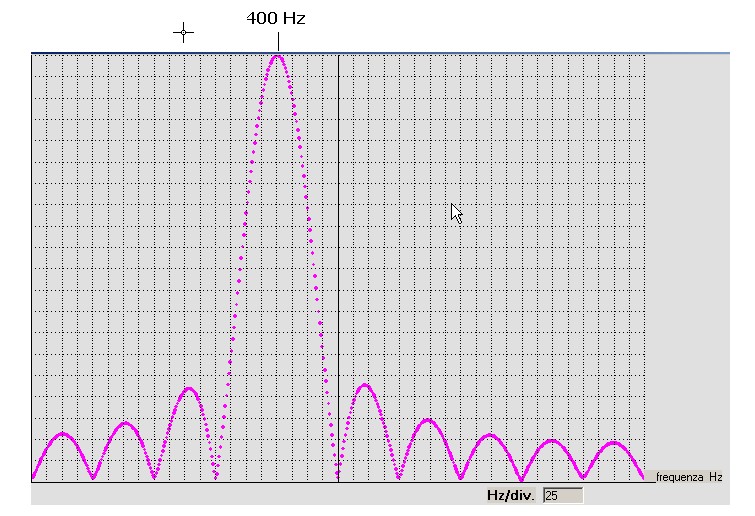 figura 25
figura 25