SONAR-INFO-p233
Calcolatore della serie di Fourier
-Processo di approssimazione-
1) La serie di Fourier in poche figure 2) Il pannello operativo del calcolatore della serie di Fourier 3)Primo esempio di calcolo della serie di Fourier con controllo analitico 4)Secondo esempio di calcolo della serie di Fourier con controllo analitico 5)Esempio di calcolo della serie di Fourier di un'onda generica 5)Esempio di calcolo della serie di Fourier di un'onda precostruita
 figura 1
figura 1
questo consente, per via esclusivamente analitica, lo studio dei fenomeni periodici funzioni
del tempo
f(x) ( dove x = 2 π f t ), quali ad esempio il segnale periodico F(x), onda rettangolare,
espresso matematicamente secondo figura 2a
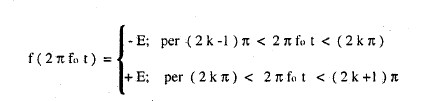 figura 2a
figura 2a
il cui andamento è tracciato in figura 2b
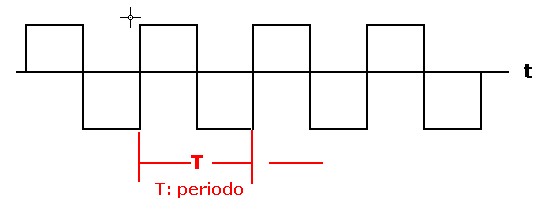 figura 2b
figura 2b
L'impiego della serie di Fourier porta alla determinazione dello spettro di frequenza a righe G ( w ), dell'onda di figura 2b,
così come mostrato in figura 3.
 figura 3
figura 3
Se dell'onda da analizzare non si conosce la legge F(t), come ad esempio per la curva di
figura 4:
 figura 4
figura 4
la serie di Fourier non è applicabile; è sostituibile, con buona approssimazione,
dall'algoritmo di figura 5 che prevede la determinazione dello spettro mediante l'elaborazione dei coefficienti
An' e Bn' da " m " campioni di F(t), messi a calcolo, rilevati da grafici o da presentazioni su oscilloscopio:
 figura 5
figura 5
Si osservi che:
a) I coefficienti di figura 5 sono indicati con A'n e B'n per distinguerli da quelli diversi di figura 1.
b) A'o, A'n, B'n sono determinati con processo numerico iterativo implementando nel programma di calcolo le
funzioni esposte in figura 5a dove, ad esempio, 20 campioni del periodo in analisi sono riportati in memoria
con i simboli
a(1).....a(20) .
 figura 5a
figura 5a
c) Il modulo della n esima riga dello spettro è indicato da C'n; nel calcolatore i valori C'n sono valutati
snza l'addizione di A'o che viene calcolato separatamente.
Vedremo di seguito, in dettaglio, l'impiego degli algoritmi di figure 5 e 5a contestualmente all'esame del pannello
operativo del calcolatore.
 figura 6
figura 6
Sezione 1 (Variabili di calcolo) :
La sezione contiene 4 textbox nei quali inserire, l'una dopo l'altra, le seguenti variabili:
-Durata del periodo dell'onda da analizzare espressa con T (Sec.).
-Il numero "m" dei campioni da prelevare dal periodo dell'onda da analizzare.
-Il numero "k" delle righe dello spettro che si vogliono calcolare.
-L'incremento di calcolo "dm" dal quale dipendono sia la precisione che il tempo calcolo.
Il pulsante "Ingresso variabili" per l'avvio dei primi calcoli.
Al lancio del programma la sezione è impostata, in via provvisoria, con i valori:
T = 0.01 Sec. ; m = 20 ; k = 10; dm = 0.01.
Sezione 2: (Campioni nel periodo)
La sezione contiene un label, a sinistra, che indica il numero progressivo dei campioni ricavati dal periodo
da analizzare e un textbox, a destra, per l'inserzione delle ampiezze dei diversi campioni.
Un pulsante "Ingresso campioni" per l'inserzione progressiva dei valori sopra citati;il pulsante presenta colore
verde nella fase d'introduzione campioni, cambia colore in arancio una volta che i campioni
dell'onda sono pari al valore impostato di " m "
Un pulsante " Azzeramento memorie" per la ripetizione, se necessario, dell'inserzione dati.
Sezione 3: ( Presentazione spettro)
La sezione contiene il pulsante "Calcolo dello spettro" per l'avvio del programma di
calcolo per:
La presentazione grafica del modulo delle righe dello spettro tracciate come visione indicativa dello stesso.
Un listato numerico delle frequenze e relative ampiezze normalizzate delle righe dello spettro.
L'azione di questo comando provoca inoltre il tracciamento del periodo dell'onda
inserito a campioni nella sezione 2 per un controllo della correttezza del suo profilo.
Sezione 4: (Listato valori calcolati)
Nel listato compaiono le "n" coppie calcolate nella forma, ad esempio per una generica 3^ coppia,
F = 1300 C'3 = 0.65432; ciascuna coppia definisce una riga dello spettro sia in frequenza che in ampiezza normalizzata.
In alto, all'esterno del listato, il valore calcolato di C'o ( componente continua dell'onda ove sia presente )
Sezione 5: (Area di presentazione grafici)
In alto lo spettro dell'onda con le " n " righe messe a calcolo.
In basso il profilo
del periodo dell'onda definito con tanti punti quanti soni gli " m " campioni messi a calcolo.
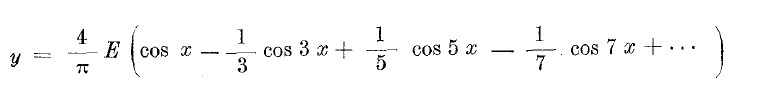 figura 7
figura 7
Come si vede la serie analitica è formata soltanto da addendi dispari i cui coefficienti, espressi con frazioni,
sono gli analoghi dei termini Cn elaborati dal calcolatore.
Utilizziamo sempre i valori di base assegnati al calcolatore al momento dell'avvio,
come mostra la figura 8 della sezione 1.
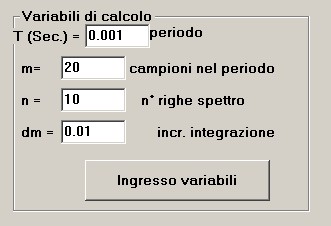 figura 8
figura 8
Quindi pigiamo il pulsante "Ingresso variabili".
Impostiamo nella sezione 2, premendo " Ingresso campioni", per lo spettro di un'onda rettangolare quale quella
riportata in figura 2b,
la seguente sequenza di campioni:
1;1;1;1;1;1;1;1;1;1; -1;-1;-1;-1;-1;-1;-1;-1:-1:-1 relativa ad un period dell'onda sopra citata fino a quando
il pulsante stesso diventa arancione.
Dopo la pressione del pulsante " Calcolo dello spettro ", si ha sia il listato dei valori così come riportato in
figura 9 che i grafici di figura 10:
 figura 9
figura 9
La lista indica righe multiple di 1000 Hz dato che, essendo T = 0.001, f = 1/ 0.001 = 1000 Hz.
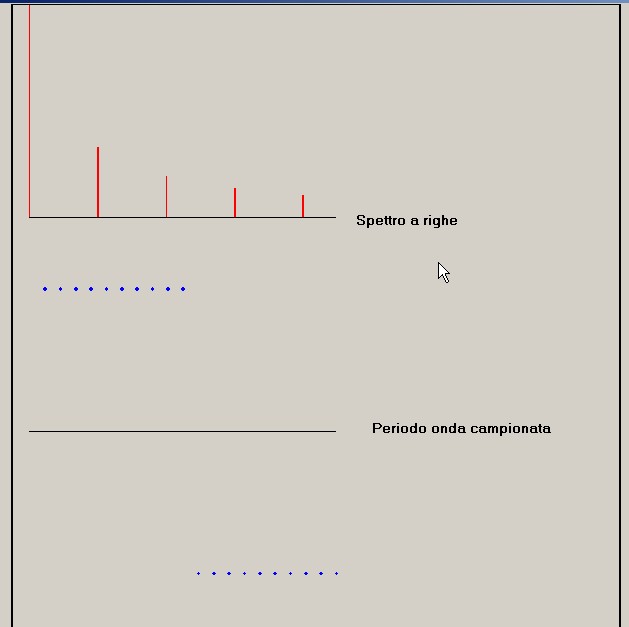 figura 10
figura 10
Procediamo ora al controllo della lista di figura 6 impostando una tabella che riporta, tanto le ampiezze dello
spettro teorico espresso in figura 7 che quelle della lista di figura 9:
Righe>
C'1
C'2
C'3
C'4
C'5
C'6
C'7
C'8
C'9
C'10
Con il calcolatore
1.0000
0.0012
0.3333
0.0012
0.2000
0.0012
0.1429
0.0012
0.1111
0.0012
Per via analitica
1.0000
0
0.3333
0
0.2000
0
0.1428
0
0.1111
0
Come si vede in tabella i valori di C'n per n dispari, praticamente coincidono, per n pari il calcolatore
commette un errore presentando ampiezze pari a 0.002 invece che 0 come da processo analitico.
Gli errori si riducono ripetendo il computo con un passo
di calcolo inferiore a dm = 0.01, ad esempio dm = 0.001; naturalmente il processo di calcolo richiede un superiore
tempo di sviluppo.
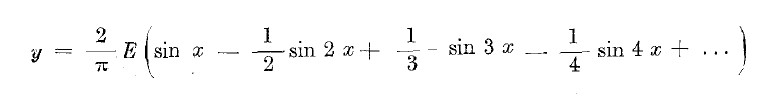 figura 11
figura 11
Come si vede la serie analitica è formata da addendi pari e dispari i cui coefficienti, espressi con frazioni,
sono gli analoghi dei termini Cn elaborati dal calcolatore.
Utilizziamo sempre i valori di base assegnati al calcolatore al momento dell'avvio,
come mostra la figura 12 della sezione 1.
 figura 12
figura 12
Quindi pigiamo il pulsante "Ingresso variabili".
Impostiamo nella sezione 2, premendo " Ingresso campioni", per lo spettro di un'onda a dente di sega quale quella
riportata in figura 13
 figura 13
figura 13
la seguente sequenza di campioni:
-1;-0.9;-0.8;-0.7;-0.6;-0.5;-0.4;-0.3;-0.2;-0.1;0;0.1;0.2;0.3;0.4;0.5;0.6;0.7:0.8:0.9 relativa ad un periodo dell'onda sopra citata fino a quando
il pulsante stesso diventa arancione.
Dopo la pressione del pulsante " Calcolo dello spettro ", si ha sia il listato dei valori così come riportato in
figura 14 che i grafici di figura 15:
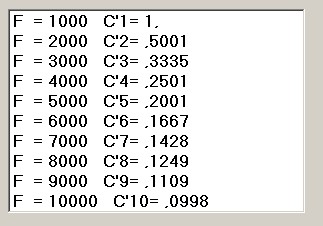 figura 14
figura 14
La lista indica righe multiple di 1000 Hz dato che, essendo T = 0.001, f = 1/ 0.001 = 1000 Hz.
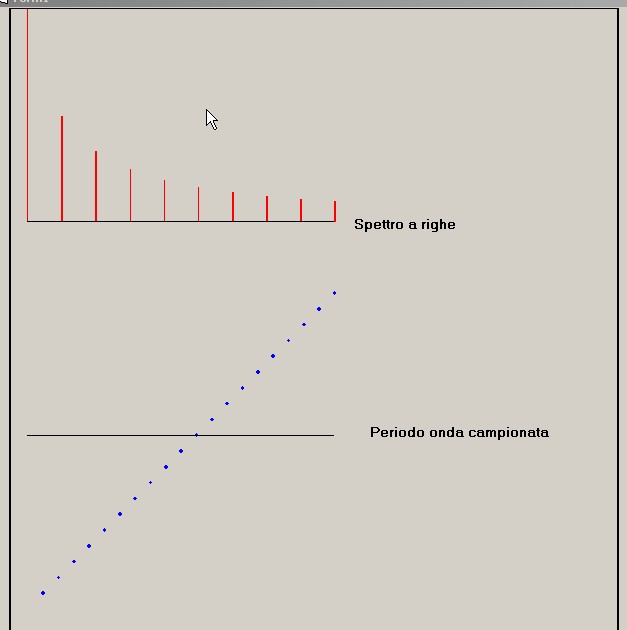 figura 15
figura 15
Procediamo ora al controllo della lista di figura 14 impostando una tabella che riporta, tanto le ampiezze dello
spettro teorico espresso in figura 11 che quelle della lista nella figura citata:
Righe>
C'1
C'2
C'3
C'4
C'5
C'6
C'7
C'8
C'9
C'10
Con il calcolatore
1.0000
0.5001
0.3335
0.2501
0.2001
0.1667
0.1428
0.1249
0.1109
0.0998
Per via analitica
1.0000
0.5000
0.3333
0.2500
0.2000
0.1666
0.1428
0.1250
0.1111
0.1000
Come si vede in tabella i valori di C' da calcolatore sono quasi coincidenti con dagli analoghi analitici; l'errore
massimo è dell'ordine del 2 per mille.
Il tracciato dell'onda sia quello riportato in figura 16:
 figura 16
figura 16
Si esegue la campionatura di un periodo con 21 campioni così come mostrato in figura 17:
 figura 17
figura 17
Si compila, in figura 18, la lista delle ampiezze dei campioni ricavandola da rilievi geometrici su figura 17:
 figura 18
figura 18
I dati di figura 18 s'inseriscono progressivamente in sezione 2 pigiando il pulsante "Ingresso campioni".
Dopo la pressione del pulsante " Calcolo dello spettro ", si ha sia il listato dei valori così come riportato in
figura 19 che i grafici di figura 20:
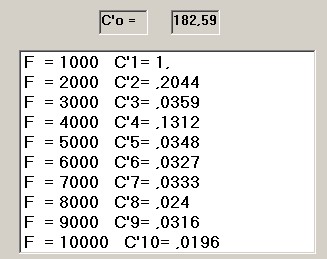 figura 19
figura 19
La lista indica righe multiple di 1000 Hz dato che, essendo T = 0.001, f = 1/ 0.001 = 1000 Hz.
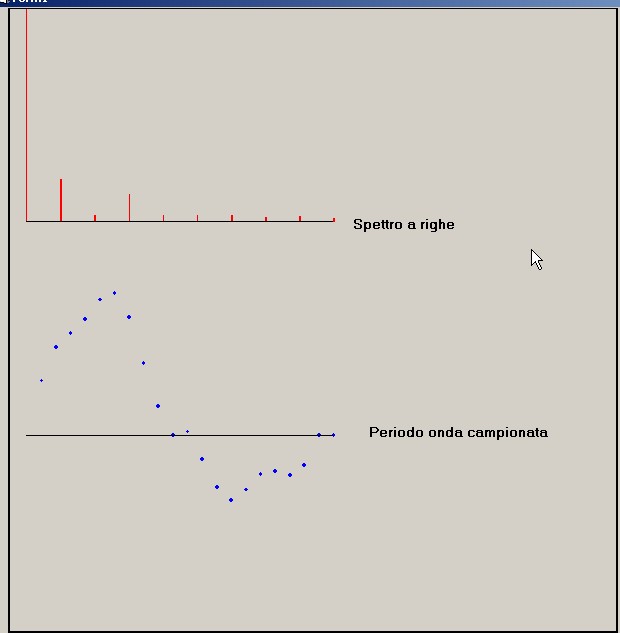 figura 20
figura 20
L'onda in oggetto, generata da un' apposita funzione matematica, è riportata in figura 21:
 figura 21
figura 21
L'onda ha un periodo T = 0.001 Sec e quindi una frequenza di 1000 Hz;
il periodo viene campionato con le stesse modalità relative al periodo dell'esercizio precedente;
il risultato della campionatura è riportato in figura 22:
 figura 22
figura 22
Seguendo la procedura d'inserzione dati e campioni analoga a quella del paragrafo precedente, dopo la
pressione del pulsante " Calcolo dello spettro ", si ha sia il listato dei valori così come riportato in
figura 23 che i grafici di figura 24:
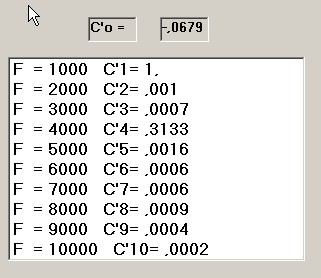 figura 23
figura 23
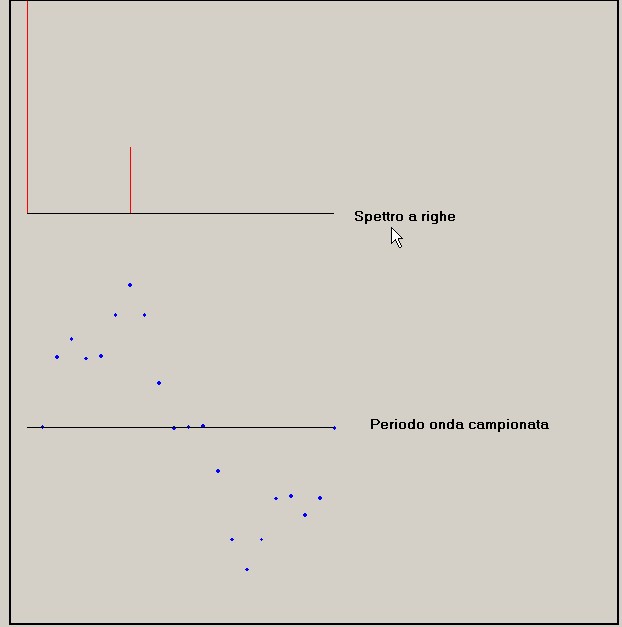 figura 24
figura 24
L'esame dei dati, sia numerici ( riga C'4 ) che grafici evidenziano, come era nelle aspettative, la presenza di
una riga a 4000 Hz di ampiezza C'4 = 0.3133.
Le righe a livello molto basso presenti in figura 23, non visibili in figura 24, sono dovute all'approssimazione
dell'algoritmo di calcolo.