1)Introduzione

Delle problematiche connesse alla misura della distanza del bersaglio si è ampiamente trattato a pagina p64; come complemento ad essa indagheremo su di una causa d'errore rilevante che incide nella metodologia operativa indicata come "misura della distanza per riflessione dal fondo", causa determinata dalla propagazione anomala del suono il cui comportamento è già strato illustrato in p24, p26, p28, p30, p226.

2)Il processo del misuratore della distanza per riflessione dal fondo

Riportiamo parte di quanto scritto nel paragrafo 5) di p64 in merito al misuratore al titolo:

Per eseguire la misura della distanza con il metodo della riflessione dal fondo si deve considerare la geometria mostrata in figura 6 nel caso che misuratore e sorgente siano alla stessa quota:



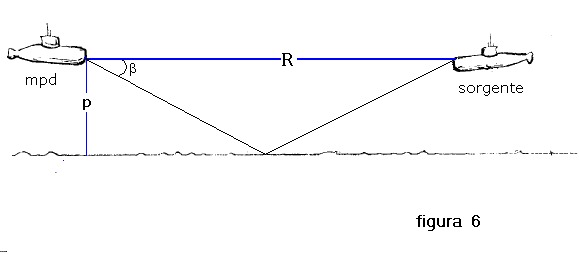
Con semplice sviluppo trigonometrico si giunge all'algoritmo di calcolo che mostriamo:

R = 2 P / tang β

dove R è la distanza dalla sorgente
P la distanza dal fondo
β è l'angolo di depressione

Nel caso più generale che il misuratore e la sorgente non siano alla stessa quota la procedura di calcolo introduce un errore che è funzione, sia della differenza di quota (dq) tra i due, sia della distanza R = f(β).
Dall'esame della figura 6/a si ricava l'espressione che indica l'errore percentuale (ep) commesso in funzione del (dq) ed R = f(β):



k = dq / Tan(β)
R1 = √[(R - k)² + dq²]
ep = 100 (R - R1) / R

Ad esempio:
ipotizzando una profondità P = 3000 m; con β = 16°; il misuratore passivo indicherà:
R = 21000 m; mentre, per la presenza della differenza di quota dq = 300 m, il valore reale della distanza dalla sorgente sarà R1 = 19890 con un errore del 5% rispetto al valore misurato.

In fase operativa l'errore ep può essere minimizzato mediante l'introduzione, a calcolo, del valore stimato di dq.

3)Sull'errore dovuto alla propagazione del suono

Facendo riferimento alla figura 6 di p64, mostrata in precedenza, vediamo come i raggi acustici si deformino in presenza di propagazione anomala; in figura 1 due condizioni a confronto; in alto il caso di propagazione normale, in basso il caso di propagazione anomala; come si vede dalla seconda figura la curvatura dei raggi, a parità dell'angolo β, fa sì che si riceva il rumore emesso dalla sorgente ad una distanza R' < R anche se a calcolo, secondo il paragrafo 2, risulterebbe sempre R = 2 P / tang β


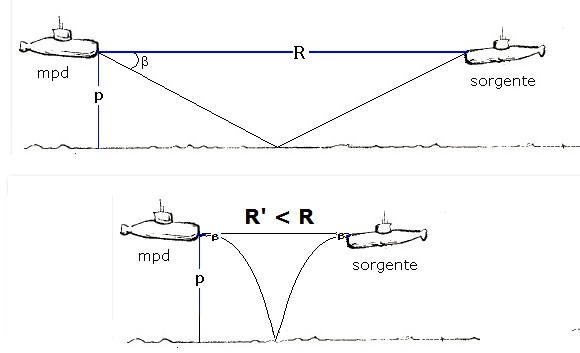
figura 1

L'entità dell'errore dipende, come vedremo, dall'ampiezza di β; la legge matematica di tale dipendenza non è proponibile data la sua complessità, cercheremo, nel successivo paragrafo, di avere un'idea in modo empirico dell' errore commesso a seguito del fenomeno della propagazione anomala.

4) Il tracciamento di curve tipiche di propagazione

Avvalendoci del software indicato in p226 ricaviamo una serie di curve attinenti tutte al batitvelocigramma riportato in figura 2 preso come modello casuale su innumerevoli disponibili.


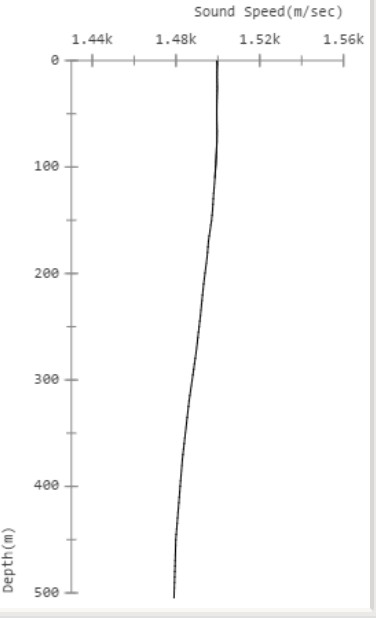
figura 2

I risultati numerici ai quali perverremo saranno risultato del bativelocigramma citato, ad altro bativelocigramma corrisponderanno risultati diversi ma sempre indicativi della problematica oggetto di questa pagina.

I percorsi dei raggi acustici sono tracciati per le seguenti variabili:
Distanza massima = 20000 m
Profondità massima = 500 m
Quota sorgente = 40 m
Numero raggi = 1
Angoli di radenza: 2°; 4°; 6°; 8°; 10°; 12°: 14°
I percorsi dei raggi sono mostrati di seguito nell'insieme di figura 3.

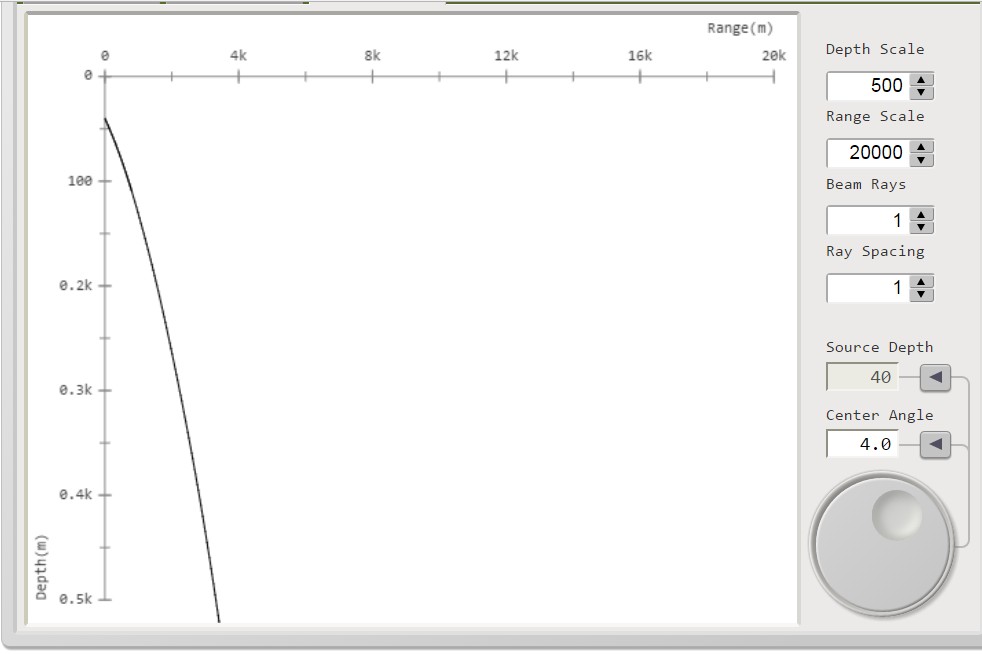
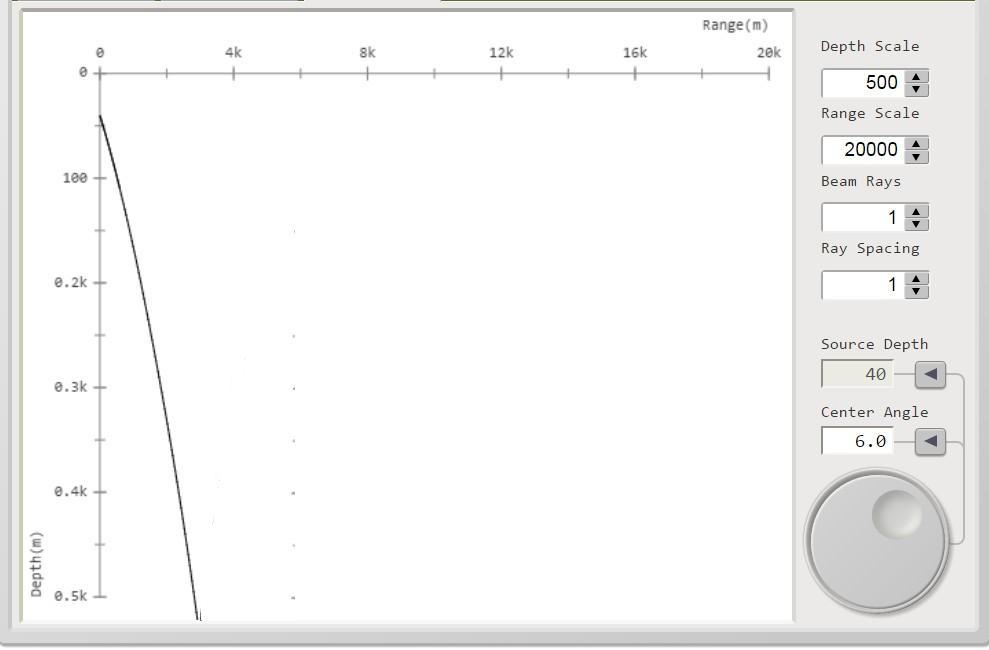figura 3


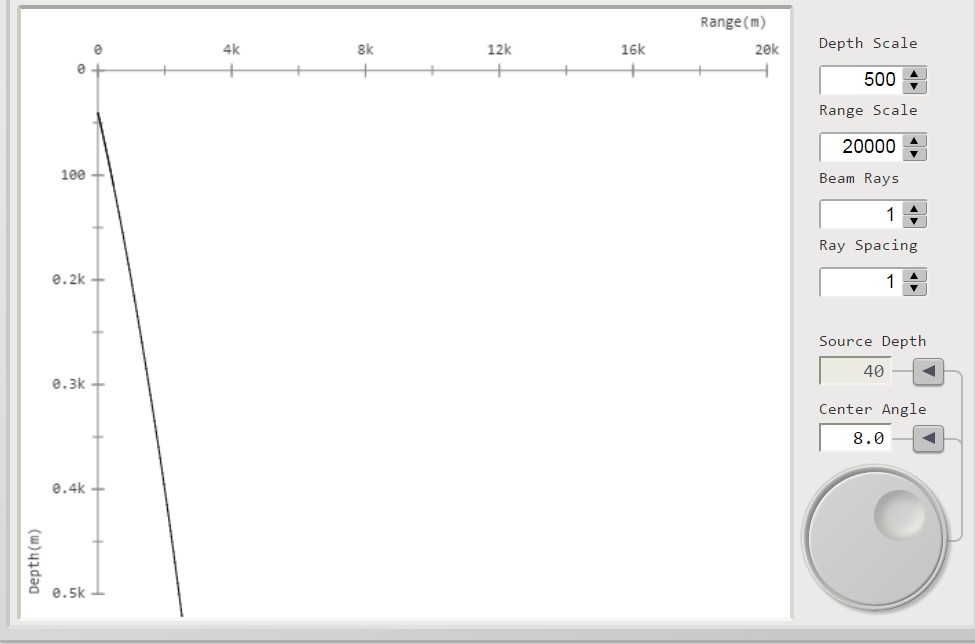
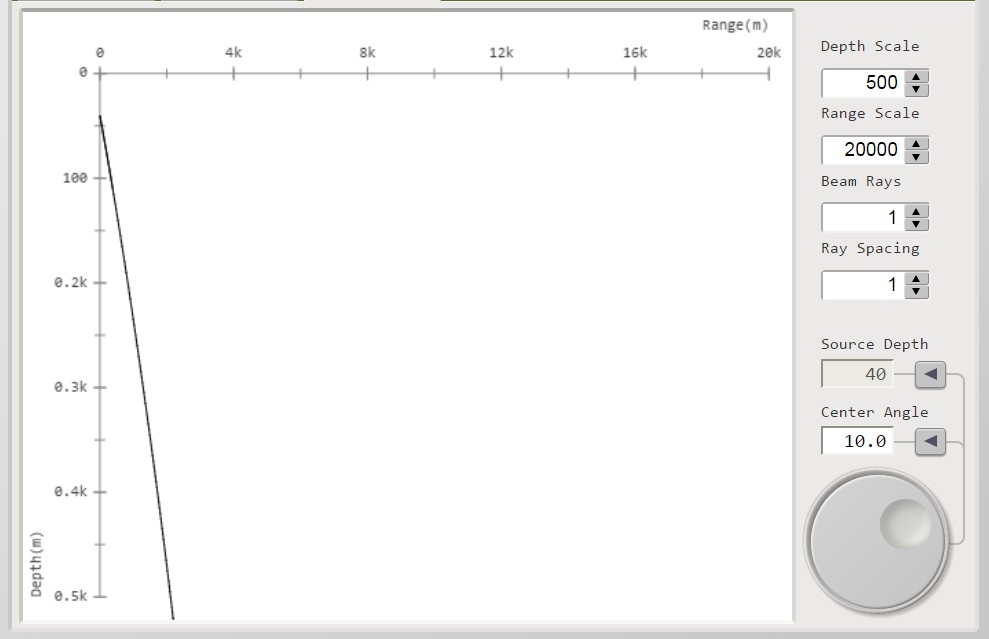
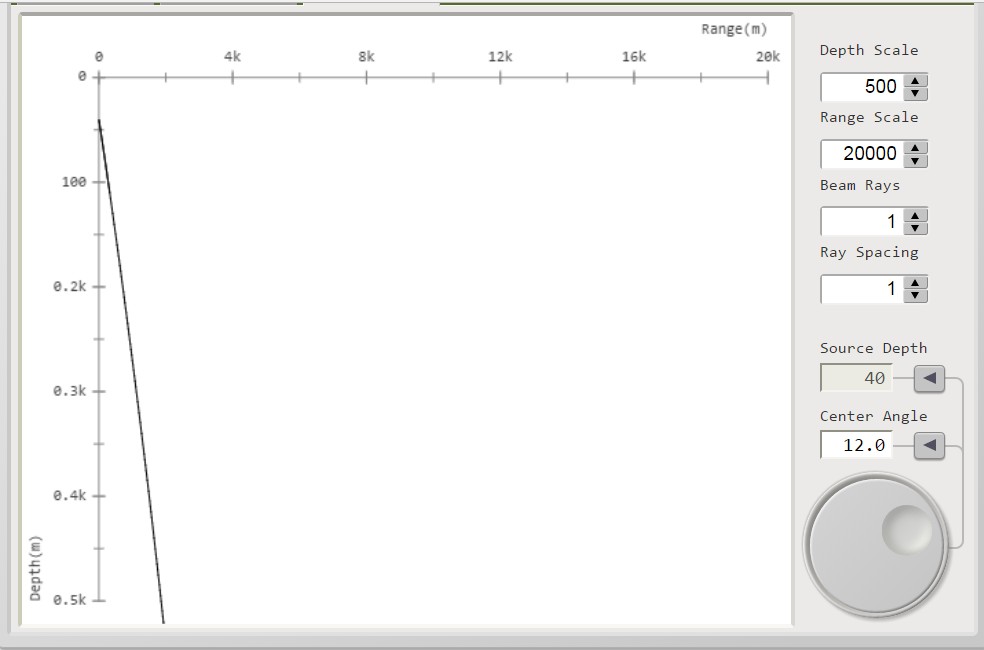
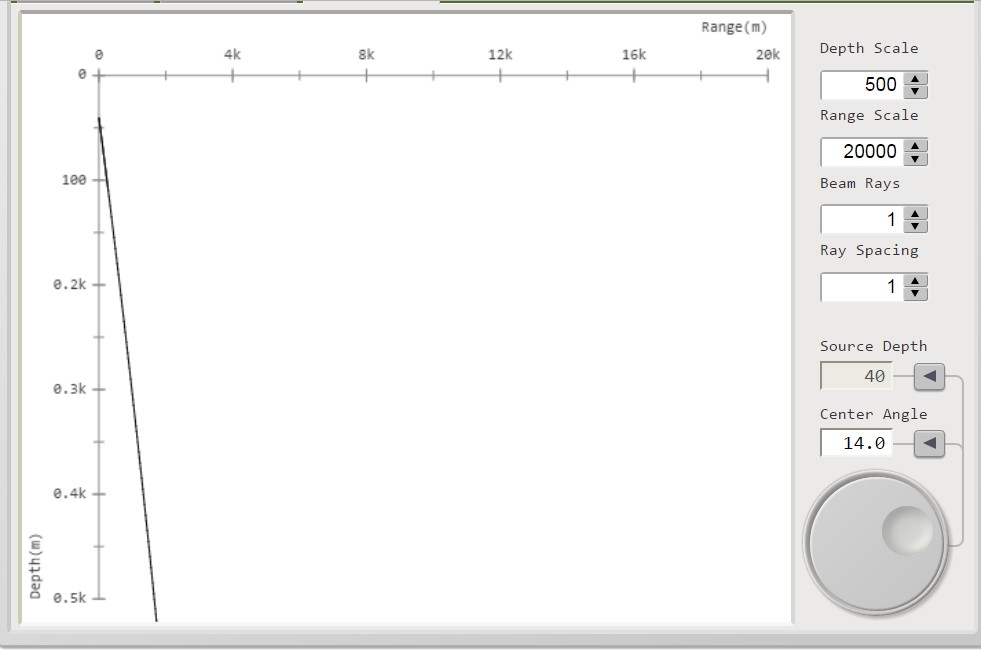
Se consideriamo il fondale a circa 500 m i raggi delle 7 curve, che impattano sul fondo, saranno riflessi verso la superficie secondo la serie di curve ricostruite di figura 4:

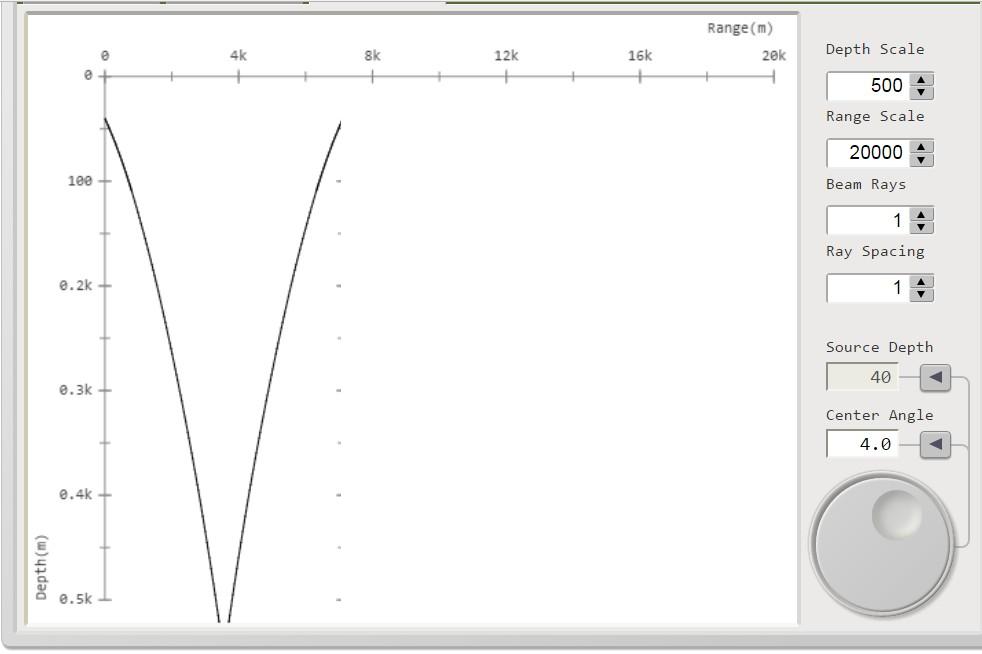
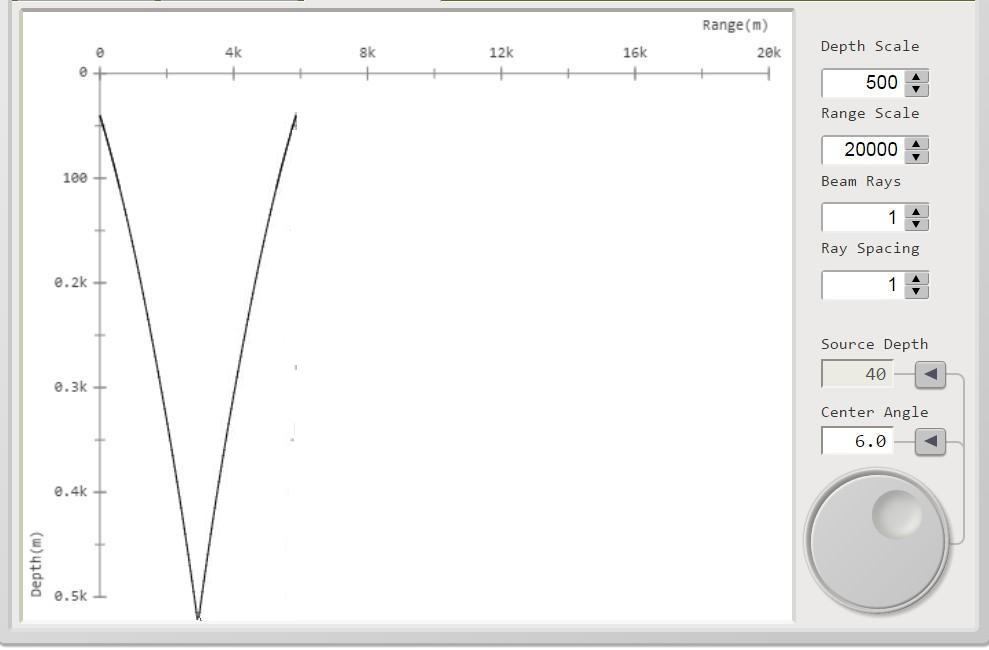figura 4


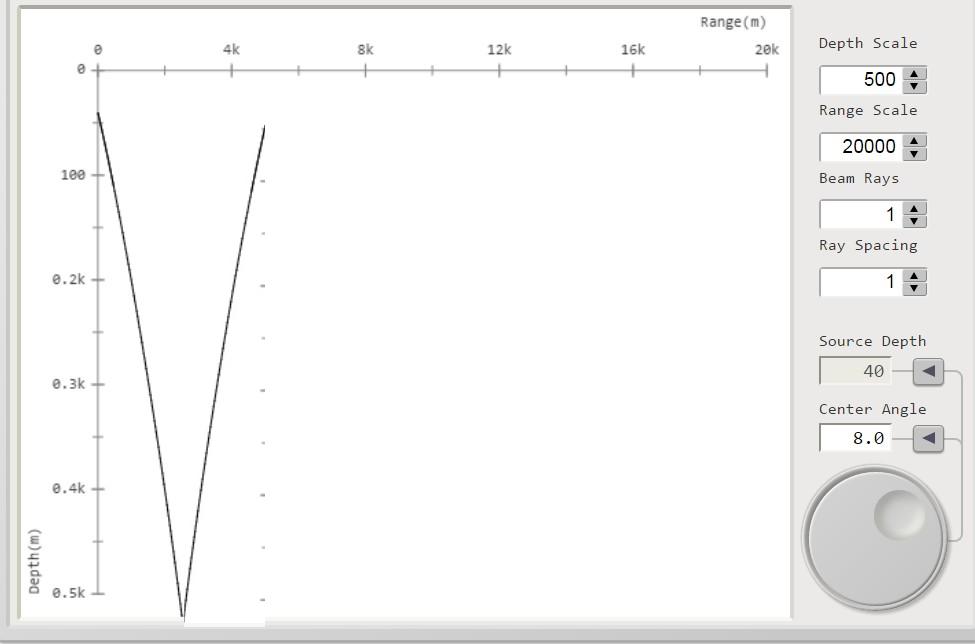
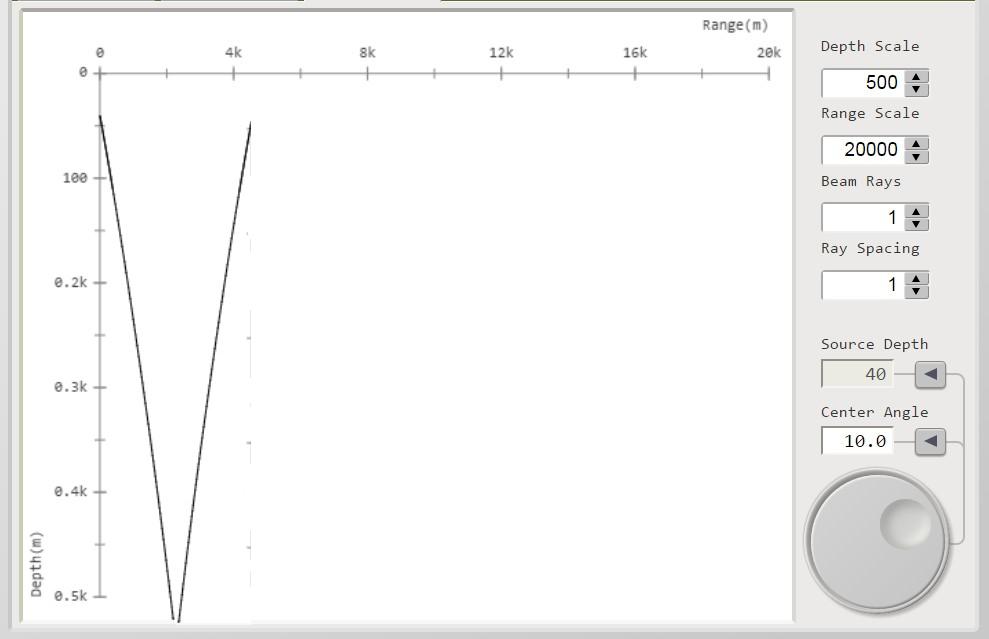
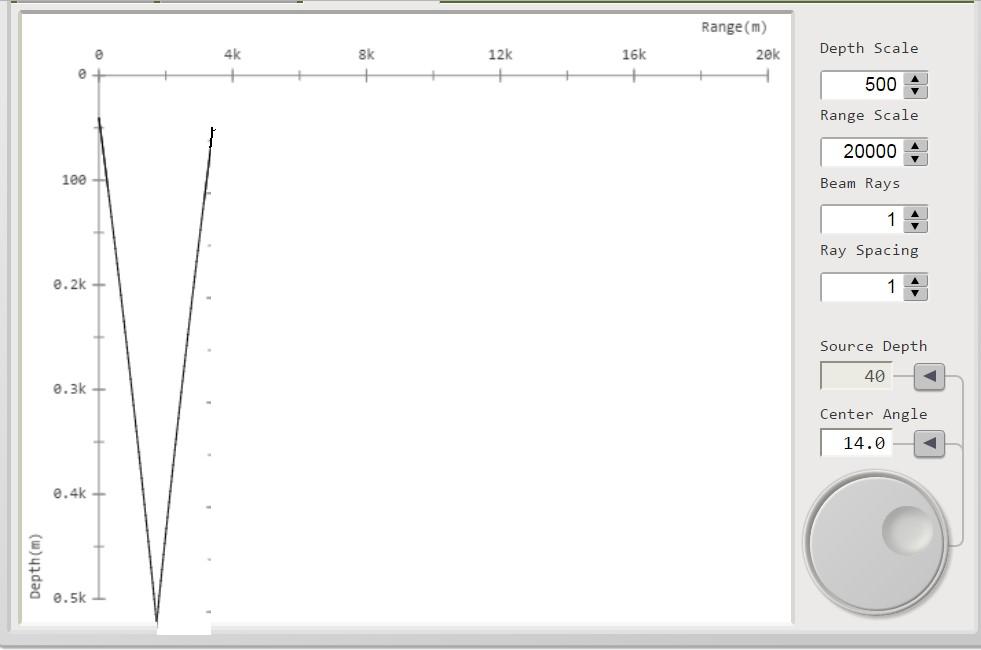
Se ora su ciascuna curva della serie di figura 4 tracciamo il percorso di un raggio acustico che parte con lo stesso angolo di radenza, supponendo per esso una propagazione di tipo normale (condizioni batitermiche ideali: costanti con la profondità) si ha la serie delle figure:
5; 6; 7; 8; 9; 10; 11 dove il raggi in oggetto sono tracciati in rosso e il fondo del mare con tratto marrone:

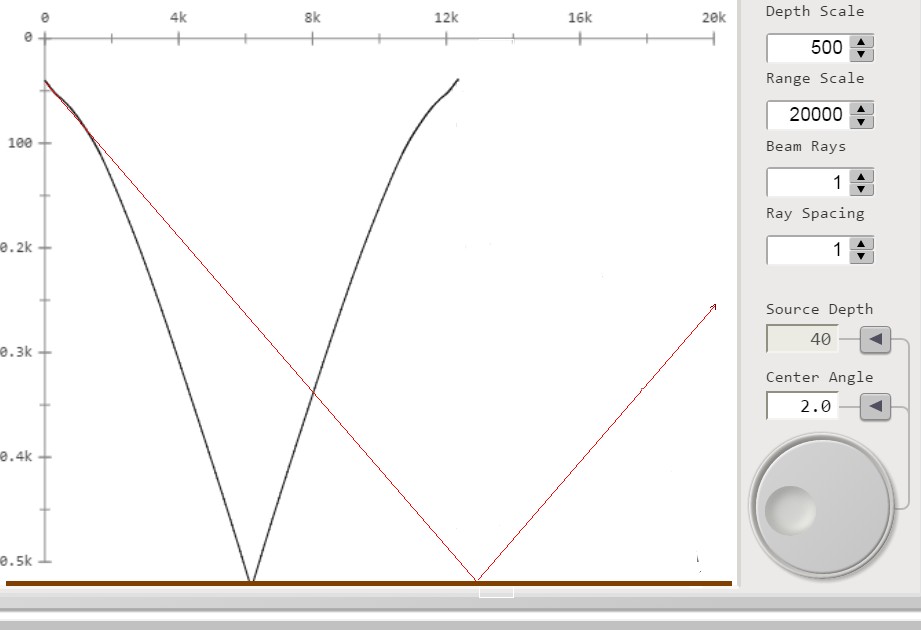figura 5; β = 2°

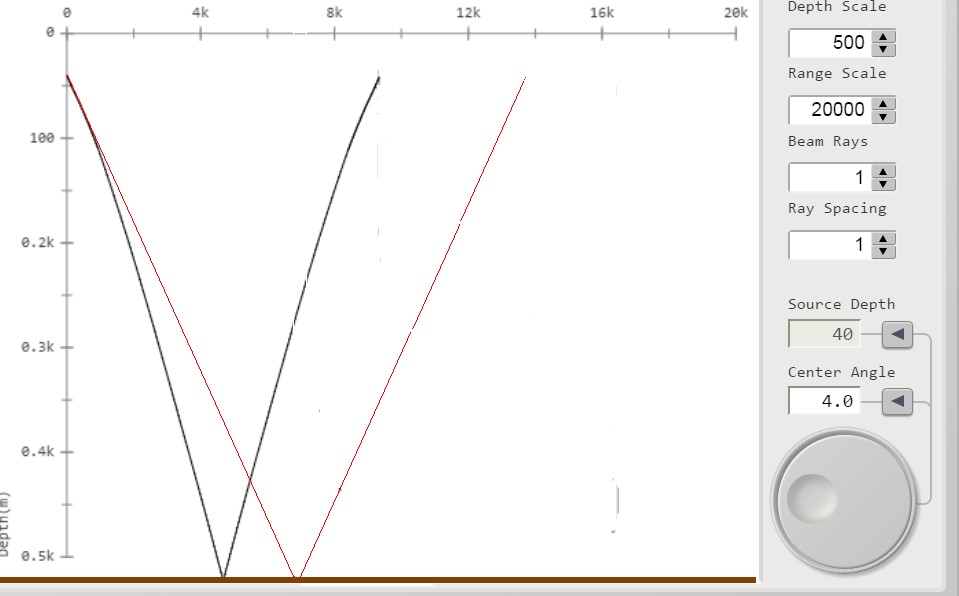figura 6; β = 4°

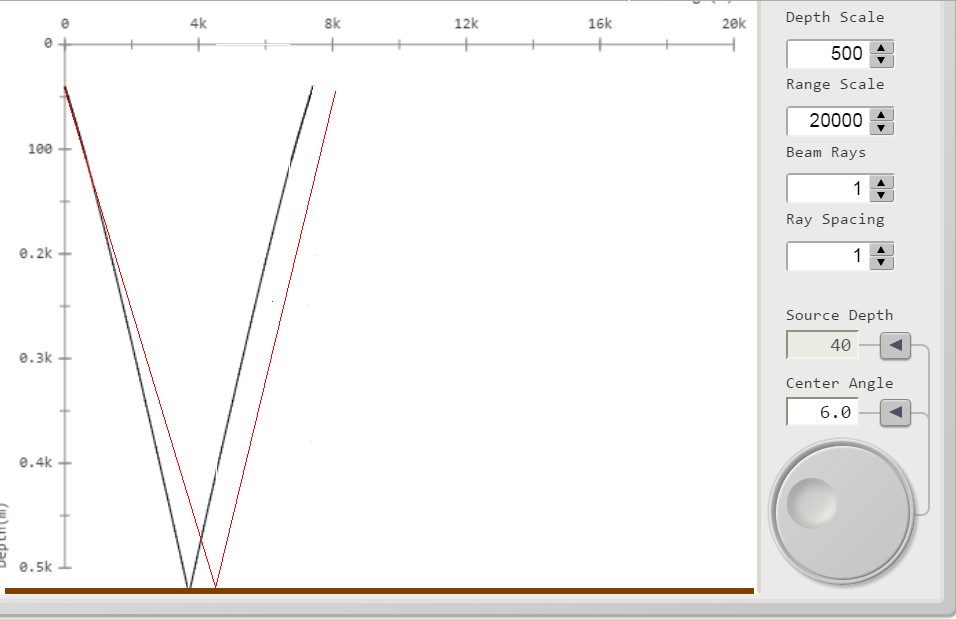figura 7; β = 6°br>
figura 8; β = 8°

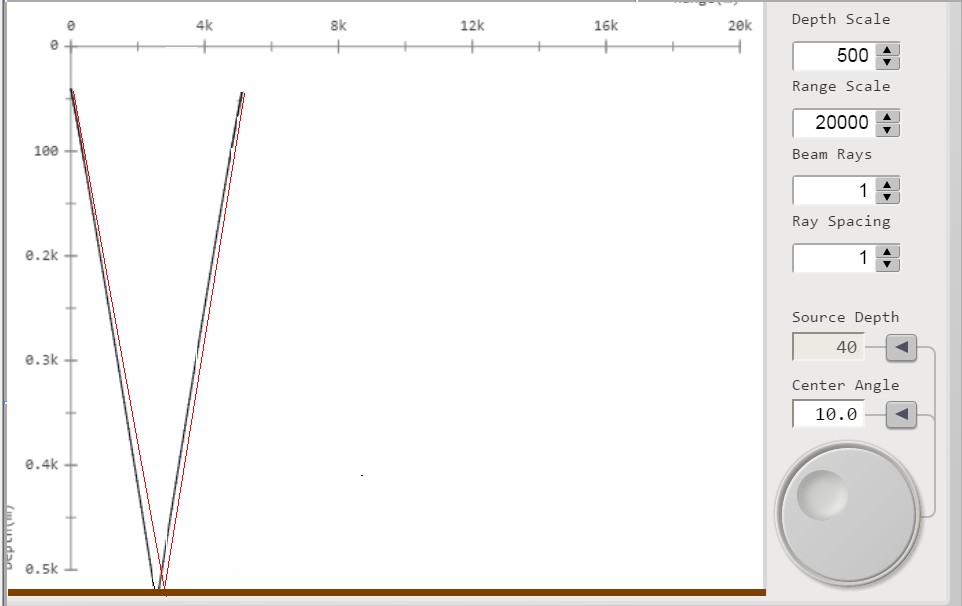figura 9; β = 10°

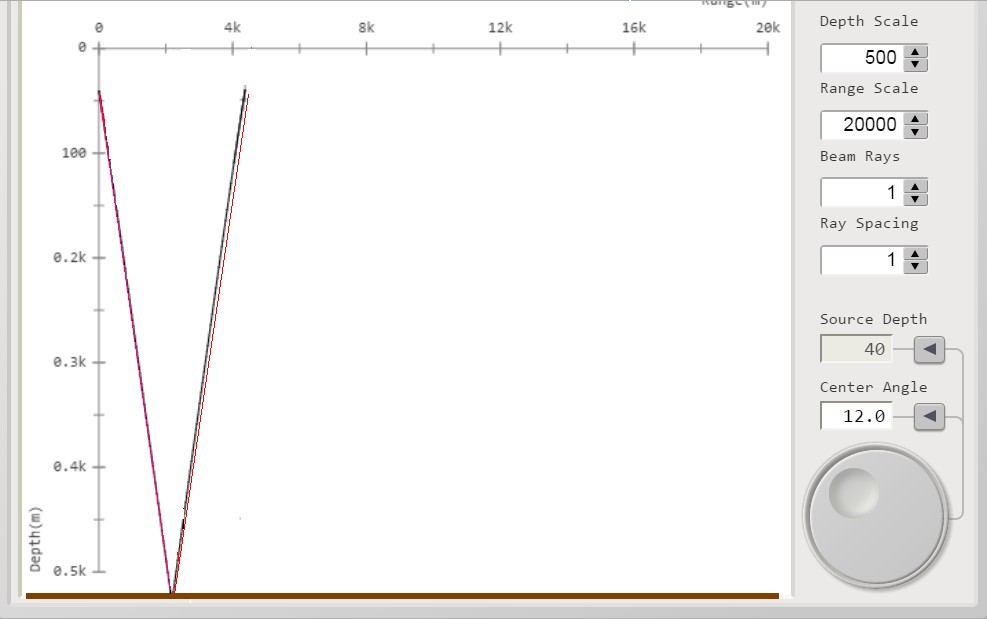figura 10; β = 12°

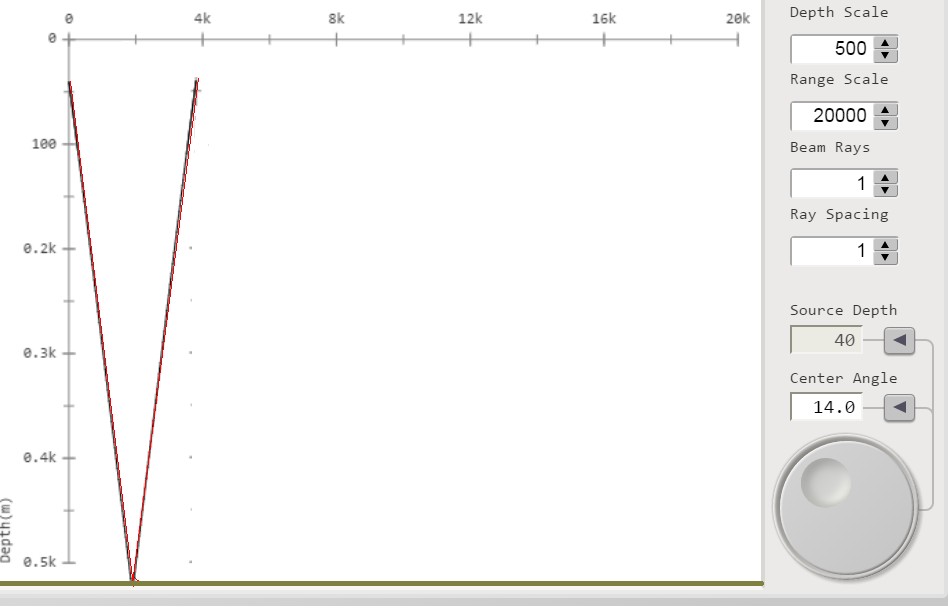figura 11; β = 14°

Se ora andiamo a valutare la distanza tra la sorgente e l'estremo del raggio riflesso dal fondo che raggiunge la quota della sorgente stessa possiamo compilare la tabella di confronto tra le distanze calcolate secondo
R = 2 P / tang β, per le traiettorie rosse e le distanze valutate sui grafici delle traiettorie nere:

I valori degli errori percentuali indicati in tabella sono riportati nel grafico di figura 12 per consentire l'interpolazione per valori intermedi dell'angolo di radenza:

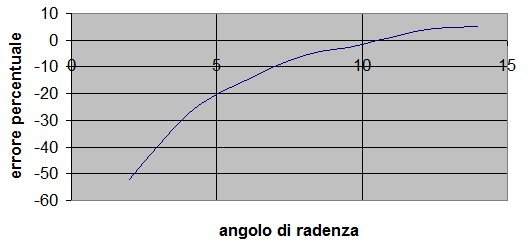figura 12

5)Considerazioni

Con l'entità degli errori emersa dall'analisi sviluppata, in base alla caratteristica specifica del bativelocigramma di figura 2, si comprende che a distanze elevate, per angoli di sito inferiori a 6°; 8° il misuratore passivo non è utilizzabile per errori di misura troppo elevati.
Con diversi profili bativelocigrafici gli errori di misura della distanza potrebbero variare in più od in meno rispetto ai valori ricavati nel paragrafo 4.
Naturalmente se il bativelocigramma porta a zone d'ombra, all'interno di queste le misure non sono fattibili.
E' chiaro quindi che per l'impiego del misuratore passivo della distanza per riflessione dal fondo deve essere cercato un sito adatto nel quale poter trovare condizioni bativelocigrafiche favorevoli al tracciamento raggi tali da minimizzare gli errori di misura.



Home