1)Introduzione

Questa pagina è dedicata ad un argomento poco conosciuto; la misura della quota dei bersagli e gli errori nella misura generati dalla propagazione anomala.
La misura della quota interessa, prevalentemente, le azioni operative di attacco nelle quali la distanza del bersaglio è contenuta in alcune migliaia di metri.
Vediamo quindi sotto questi aspetti come si sviluppa la procedura di misura e come si valutano gli errori conseguenti alla propagazione del suono.

2)Il processo del misuratore di quota

La misura della quota di un bersaglio è affidata al rilevamento, nel piano verticale, delle variabili R e β così come mostra la figura 1:

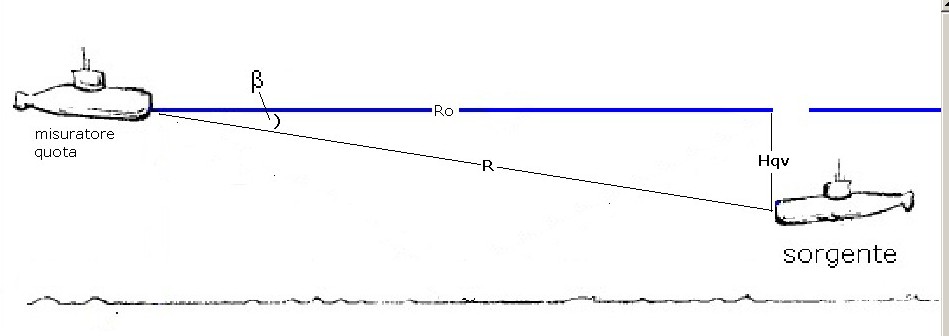Figura 1

La quota Hqv (quota virtuale) è calcolata in funzione di R e β secondo la semplice espressione:

Hqv = R Sen(β) ; equazione 1)

valida soltanto in condizioni di propagazione ideale; le due variabili R e β possono essere rilevate come segue:

La distanza R può essere calcolata, o con il metodo dell'eco (sonar attivo - vedi p2, cap5, par 5.3) o con un misuratore passivo della distanza come riportato in p64.
L'angolo β può essere rilevato da un sistema a fasci preformati (vedi p94), collegato ad una base sferica, vedi figura 2; con i fasci che si sviluppano nel piano verticale:

Figura 2

3)Gli errori sulla misura della quota causati dalla propagazione anomala

Per affrontare questo argomento prendiamo, ad esempio, il modello di propagazione calcolato e tracciato nello studio di p28 e di seguito riportato in figura 3:

Figura 3

Le variabili utilizzate nel grafico sono espresse con unità di misura anglosassoni:
Temperature: (°F ) in gradi Fahrenheit ( °F = °C x 9/5 + 32)
Profondità: (ft) in feet ( ft = mt x 3.281 )
Distanze: (yd) in yard (yd = m x 1.094 )

Nel diagramma di sinistra è mostrato un batitermogramma tipico nel quale si ha temperatura costante da quota 0 a quota 64 ft e temperatura decrescente in modo lineare da 64 ft in poi; come è noto a questo corrisponde il diagramma relativo alla velocità del suono (il bativelocigramma).
Nel diagramma di destra è tracciato un raggio acustico che si propaga dall'origine fino ad una distanza Ro ≈ 2800 Yd; nel tratto compreso tra la sorgente e quota 64 ft il raggio curva leggermente dato il modesto gradiente della velocitè del suono dovuto alla pressione, sotto quota 64 ft il raggio piega vistosamente a causa del sensibile gradiente della velocità del suono a seguito della variazione di temperatura per le quote oltre i 64 ft. Nel calcolo della curva l'angolo di radenza del primo tratto del raggio è di 0.012 radianti.

Con i dati esposti procediamo al calcolo della quota Hqv di un generico bersaglio che si veda sotto un angolo β= 0.012 radianti ad una distanza a piacere Ro in Yd:
Dalla figura 1 possiamo scrivere una seconda equazione, equivalente alla 1), per il calcolo di Hqv in funzione di Ro e β:

Hqv = Ro Tang (β) ; equazione 2)

Se assumiamo ad esempio Ro = 2200 Yd il valore di Hqv espresso in Yd sarà:
Hqv = 2200 Tang(0.012rad) = 26.4 Yd pari a 86 ft.
Se tracciamo quest'ordinata nel diagramma di figura 3, all'ascissa Ro = 2200 Yd, e la congiungiamo con l'origine abbiamo la figura 4 nella quale si confronta il percorso di un raggio acustico in ambiente ideale a velocità del suono costante con un raggio in ambiente anomalo che parte con lo stesso angolo di radenza β.

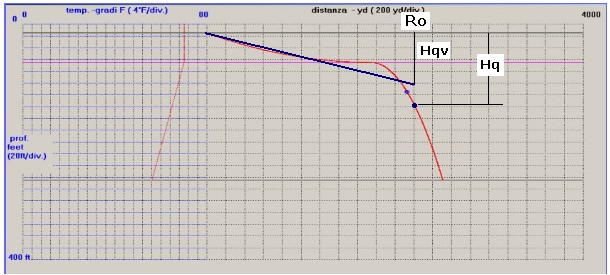Figura 4

Dalla figura si vede la differenza tra la quota virtuale Hqv pari a 86 ft, ottenuta dal calcolo, e la quota reale Hq di 120 ft dovuta al percorso anomalo del raggio; questo esempio mostra un errore di quota dell'ordine del 50 %.

In altri termini ed altre unità di misura, se la curva di propagazione fosse quella di figura 4, qualora si puntasse il bersaglio sul piano verticale con un angolo di 0.68° ad una distanza Ro = 2011 m , il calcolo porterebbe ad una quota di 26 m mentre in realtà il bersaglio si troverebbe a quota 39 m.
Questo ed altri innumerevoli esempi possono essere sviluppati; è chiaro che la misura della quota di un bersaglio è molto critica e devono essere prese tutte attenzioni del caso per tener conto della curvatura dei raggi dovuta alle variazioni della velocità del suono in acqua.



Home