1) Generalità
Della trasformata di Hilbert si è accennato a pagina p5; cap.5; par. 5.1 nel trattare dei correlatori speciali, il sistema basato su questa trasformata è stato nominato come Anticorrelatore del quale si sono mostrate alcune applicazioni.
Ancora della trasformata di Hilbert, da un punto di vista applicativo, si è trattato a proposito dei sistemi d'inseguimento automatico dei bersagli alla pagina p218 .
Su questa pagina vogliamo investigare, per la prima volta, sulla trasformata da un punto di vista puramente matematico.

2) Da Fourier a Hilbert
E' comunemente acquisito il concetto di Trasformata di Fourier, sviluppata con il calcolo integrale riportato nell' algoritmo 1); algoritmo che consente la trasformazione di una funzione del tempo, ad esempio una funzione di correlazione C(t) (vedi figura 1 -sinistra-) in una funzione della frequenza: lo spettro di frequenza dei segnali che hanno originato la C(t) ( vedi figura 1 -destra-):

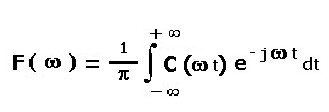1)

Con la 1) si passa dal dominio del tempo al dominio della frequenza.

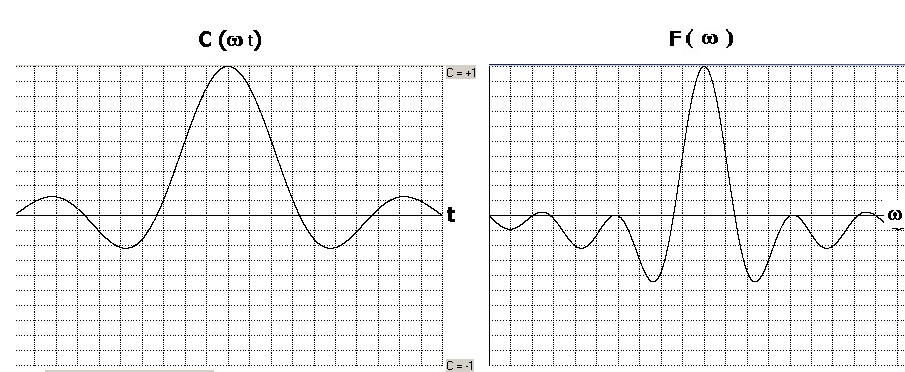figura 1

Sempre con il calcolo integrale Hilbert ha strutturato un algoritmo, indicato in 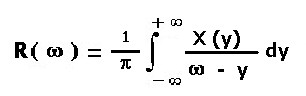2),

2)

che trasforma una funzione, ad esempio nel dominio del tempo, in una funzione diversa ma ancora nello stesso dominio; questa trasformazione nel caso che X(y) sia una funzione di correlazione C(τ), vedi figura 2 a sinistra, la 2) la trasforma in una funzione di correlazione C(τ ') , ma con tutte le frequenze dei segnali che concorrono al calcolo di C(τ) sfasate di 90° tali che l'andamento della C(τ) risulti modificato così come si vede nella C(τ ') in figura 2 a destra; la funzione trasformata di C(τ ') è indicata come
HC(τ)

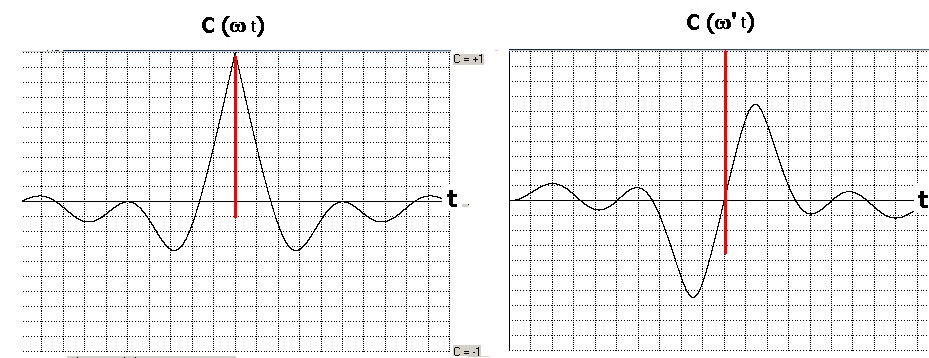figura 2

3) Le funzioni esplicite di C(τ) e HC(τ)
E' utile per il prosieguo dell'analisi esplicitare le C(τ) e le HC(τ) sia per i segnali analogici che per i segnali a due stati; tutte le funzioni illustrate sono calcolate per segnali in banda di rumore definita tra f1 e f2, per S/N = ∞, così come mostrato negli algoritmi seguenti:

Segnali analogici :

La 3) è ottenuta con processi d'integrazione così come illustrato a pagina p12:

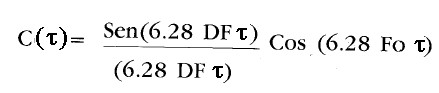3)

La 4) è la trasformata della 3) secondo la 2)

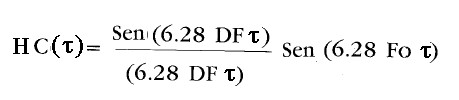4)

Segnali a due stati:

La 5) è ottenuta con processi d'integrazione così come illustrato a pagina p12:

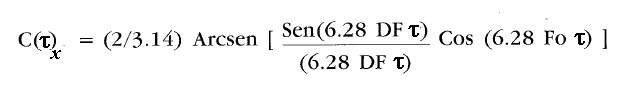5)

La 6) è la trasformata della 5) secondo la 2)

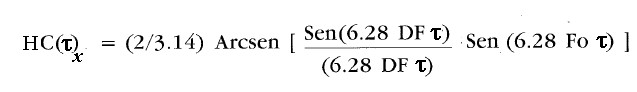6)

Sui simboli:
C(τ) = funzione di correlazione analogica in banda f1-f2
HC(τ) = funzione di correlazione analogica in banda f1-f2 trasformata con Hilbert
C(τ)x = funzione di correlazione a due stai in banda f1-f2
HC(τ)x = funzione di correlazione a due stati in banda f1-f2 trasformata con Hilbert
DF = (f2 - f1)/2
Fo = (f1 + f2)/2
τ = variabile indipendente
dove: f1 = frequenza inferiore della banda; f2 = frequenza superiore della banda.

Tutte le funzioni mostrate sono descritte ed utilizzate nel testo in p5; l'analisi delle HC(τ)x che segue è l'unica prerogativa di questa pagina.

4)Analisi del profilo della HC(τ)x
L'analisi della HC(τ)x ha come obiettivo lo studio del passaggio della funzione per l'asse delle ascisse e la valutazione della sua pendenza che è di fondamentale importanza per l'impiego della funzione nelle diverse problematiche dei sonar.
Osserviamo ora, in base alla 6) che riportiamo, una delle caratteristiche della HC(τ)x :

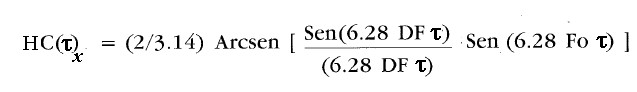6)

La HC(τ)x è di fatto l'ArcSen del prodotto di due funzioni, la 6a) e la 6b):

6a)

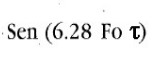6b)

Essendo Df << Fo la 6a) ha l'argomento più piccolo della 6b) quindi esercita sulla 6b una sorta di modulazione d'ampiezza così come mostra la figura 3 ottenuta per la banda f1 = 8000; f2 = 10000 : ascisse: - 500 μSec; 0 ; + 500 μSec.

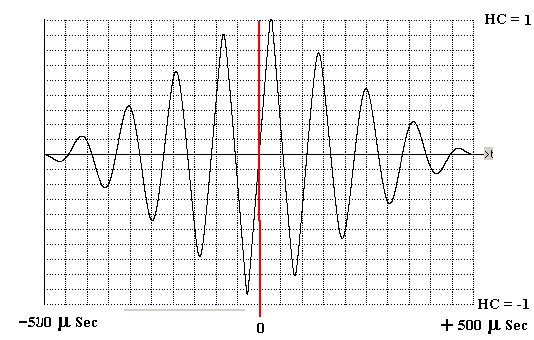figura 3

Dato che la 6a) varia di poco la sua ampiezza attorno all'ascissa di passaggio per lo zero della 6b), da 1 a 0.983 tra 0 e 50 μSec, sarà praticamente ininfluente sulla pendenza della 6b) in tale intervallo.
Questa osservazione è determinante nell'analisi della pendenza della HC(τ)x, pendenza sulla quale diverse soluzioni tecniche relative al sonar sono imperniate.

5)Analisi della pendenza della HC(τ)x
La HC(τ)x è un processo di correlazione per la rivelazione dei segnali con caratteristiche equivalenti ad altre funzioni di correlazione simili del tipo C(τ)x, la prima presenta livello 0 dove la seconda presenta il livello 1.
In ogni caso gli algoritmi sia delle HC(τ)x, sia delle C(τ)x sono normalizzati; il loro valore massimo sarà sempre l'unità.
La HC(τ)x è impiegata per la soluzione di numerose applicazioni tecniche grazie alle caratteristiche della stessa nel passaggio per l'ascissa per τ = 0;.
In dipendenza dal tipo di applicazioni deve essere stabilita la dovuta pendenza della HC(τ)x, alcune soluzioni necessitano di pendenze molto elevate, altre di pendenze medie; giova quindi calcolare le variabili che definiscono la HC(τ)x in modo che, con la loro impostazione, si possano ottenere i risultati voluti.
Sulla base di quanto osservato alla fine del paragrafo precedente possiamo riscrivere la 6) modificata come riportato in 7) ritenendola valida soltanto nell'intorno di τ = 0 :

7)valida soltanto nell'intorno di τ = 0

quindi:

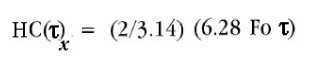8) valida soltanto nell'intorno di τ = 0

L'ampiezza della HC(τ)x, soltanto nell'intorno di τ = 0, è proporzionale a Fo con pendenza Δ espressa in: (frazioni dell'unità)/(microsecondi):

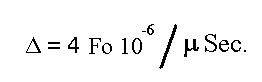9).valida soltanto nell'intorno di τ = 0

6)Esempi di calcolo
Premessa -Il calcolatore per tracciare i grafici di questo paragrafo è disponibile alla pagina p157-.
Tre esempi numerici per concludere questo lavoro:
*primo:
Calcolare e verificare graficamente il Δ di una funzione HC(τ)x per segnali nella banda: f1 = 1000 Hz; f2 = 2000 Hz:
essendo Fo = ( f1 + f2 )/2 = 1500 per la 9) si ha:
Δ = 4 Fo / 1000000 = 4 x 1500/1000000 = 0.006
Se tracciamo la HC(τ)x per la banda indicata abbiamo la figura 4 nella quale, con il Δ calcolato possiamo verificare, ad esempio, che l'ampiezza, per τ = 50 μSec., è (Δ)x(τ) = 0.006 x 50 = 0.3 così come è evidenziato, a tratto rosso, in figura:

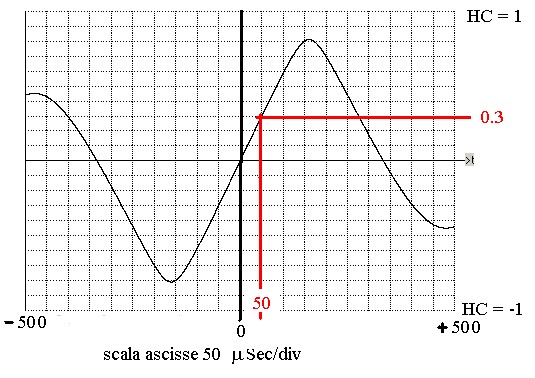figura 4

*secondo:
Sia richiesta la definizione ed il calcolo di una funzione di correlazione trasformata di Hilbert normalizzata che consenta, attorno a τ = 0 , una pendenza Δ = 0.01 / μSec.
dalla 9) ricaviamo Fo = Δ x 1000000 / 4 = 0.01 x 1000000 / 4 = 2500 Hz
I valori estremi di banda, dei quali Fo ne è la media, possono essere calcolati partendo, ad esempio fissando f1, inferiore a Fo; f1 = 1000 Hz ; f2 = 2 Fo - f1 = 4000 Hz.
Con gli estremi di frequenza calcolati tracciamo la figura 5; se il valore di Fo = 2500 Hz è corretto l'ampiezza della HC(τ)x per τ = 25 μSec.(ad esempio) sarà: (Δ) x (τ) = 0.01 x 25 = 0.25 come mostra la figura:

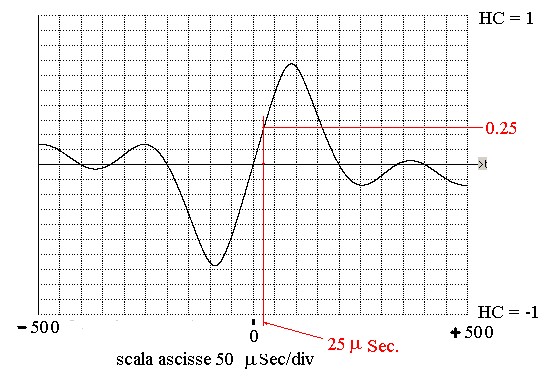figura 5

*terzo
Ancora il calcolo di Fo per una pendenza Δ = 0.1 / μSec.:
Fo = Δ x 1000000 / 4 = 0.1 x 1000000 / 4 = 25000 Hz
posto f1 = 10000 Hz si ha f2 = 40000 Hz
Se per il controllo dei valori degli estremi della banda utilizziamo per le ascisse il solito valore di 50μSec./div otteniamo il grafico di figura 6 nel quale, data la compressione della curva, non è possibile eseguire rilievi precisi:

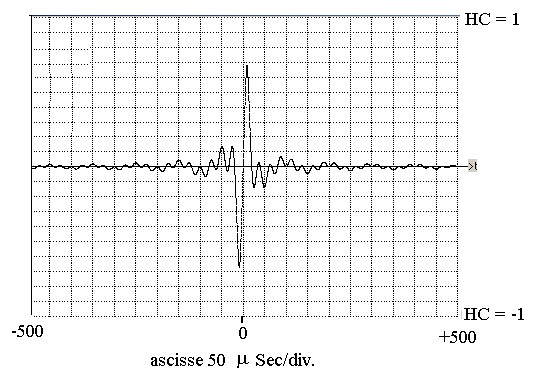figura 6

Per il controllo è necessario cambiare la scala delle ascisse da 50 μSec./div, ad esempio, a 1 μSec./div :
con questa nuova scala potremo verificare l'ampiezza della HC(τ)x per τ = 2 μSec.(ad esempio) sarà:
(Δ) x (τ) = 0.1 x 2 = 0.2 così come mostra la figura 7:

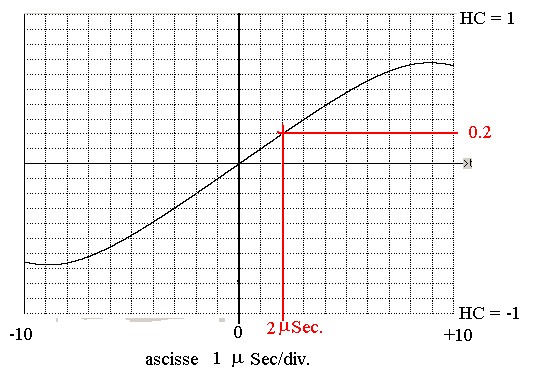figura 7