SONAR-INFO-p262
Calcolo della probabilità di scoperta
come funzione della distanza del bersaglio
1) Generalità
Il problema relativo al calcolo della probabilità di scoperta in passivo (Priv.) in funzione della distanza del bersaglio, Priv. = f (R), è molto complesso; l'interesse per questo argomento è soltanto a carattere speculativo non utile ai fini operativi sul campo.Il processo di elaborazione di Priv. = f (R) implica l'impiego del calcolatore delle curve ROC e un insieme di routine accessorie da eseguire su P.C. per le soluzioni di equazioni trascendenti con metodi iterativi.
2)Calcolo della portata di un sonar passivo di riferimento
Per sviluppare quanto accennato nelle generalità è necessario impostare il calcolo della portata di un sonar passivo di riferimento secondo la sequenza delle variabili quali ( si veda P42 ):F1 ; F2 estremi di banda delle frequenze di ricezione: F1 = 1000 Hz; F2 = 3000 Hz
fo frequenza media geometrica nella banda: fo = 1.7 KHz
SL s'ipotizza come sorgente del segnale un cacciatorpediniere di vecchia generazione che naviga a 20 nodi; dai tabulati in letteratura, per fo = 1.7 KHz, si ha: SL = 140 db/microPascal/Hz
NL s'ipotizza il mare a forza 2; dai tabulati in letteratura, per fo = 1.7 KHz, si ha:
NL = 58 dB/microPascal/Hz
DI si assume un guadagno di direttività della base ricevente di: DI = 10 dB
RC si pone a calcolo una costante di tempo d'integrazione di: RC = 0.1 Sec.
d si stabilisce di avere una probabilità di scoperta del 99% con una probabilità di falso allarme del 0.1 %; d = 28
Propagazione s'ipotizza di operare a quote profonde con: propagazione sferica
BW la larghezza di banda del ricevitore è: BW = F2-F1 = 2000 Hz
DT il valore del DT calcolato con la formula riportata in p42 è: DT = 27.2 dB
Con i dati impostati si applica l'equazione 1) ottenendo:
1) TL = SL + DI - NL - DT + 10 Log BW = 140 dB + 10 dB - 58 dB - 27.2 dB + 10 Log 2000 = 97.8 dB
Dopo il calcolo del TL secondo la 1) si computa ora la variazione del TL in funzione della distanza R e del coefficiente di assorbimento "a" ottenendo la 2):
2) TL = 60 dB + 20 Log R + a R = 60 dB + 20 Log R + 0.1 R
dove il valore di "a" ,calcolato con la formula riportata in p42, è: a = 0.1 dB/Km
La soluzione del sistema tra la 1) e la 2) porta ad un valore di R = 46 Km.
Questo esercizio mostra come, con le variabili indicate per i calcoli della portata, alla coppia Priv = 99% e Pfa. = 0.1% corrisponda un valore della distanza di R = 46 Km; per valori crescenti di questa distanza calcoleremo la riduzione della probabilità di rivelazione (Priv.) di questo sonar di riferimento.
3)Processo di calcolo di Priv. = f (R)
Il computo della funzione Priv. = f (R) inizia con la stesura di una tabella da ricavarsi con il calcolatore curve ROC di P80.Fissato il valore di Pfa. = 0.1 %, come da sonar di riferimento, si computano 20 valori del parametro "d" per altrettanti valori di Priv. da Priv = 5% a Priv = 99% a passi del 5%, dopo lungo e complesso lavoro il calcolatore ROC fornisce tutti i dati per compilare la tabella:
| Priv. % | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 99 |
| "d" | 1.8 | 2.9 | 3.8 | 4.7 | 5.4 | 6.1 | 6.8 | 7.6 | 8.3 | 9 | 9.8 | 10 | 11 | 12 | 13 | 14 | 16 | 18 | 21 | 28 |
Alla prima tabella segue la seconda nella quale, sempre secondo le variabili del sonar di riferimento, si calcola il valore del DT in funzione del "d" ricavato da tab.1 [DT = f (d)] secondo l'espressione:
DT = 5 Log[ d BW / (2 RC) ]
| "d" | 1.8 | 2.9 | 3.8 | 4.7 | 5.4 | 6.1 | 6.8 | 7.6 | 8.3 | 9 | 9.8 | 10 | 11 | 12 | 13 | 14 | 16 | 18 | 21 | 28 |
| DT | 21.3 | 22.3 | 22.9 | 23.4 | 23.7 | 24 | 24.2 | 24.4 | 24.6 | 24.8 | 24.9 | 25 | 25.2 | 25.4 | 25.6 | 25.7 | 26 | 26.3 | 26.6 | 27.2 |
Con i valori del DT della tab.2, secondo l'equazione:
60 + 20 log R + 0.1 R = SL + DI - NL - DT + 10 log BW
che in base ai dati del sonar di riferimento ed esplicitata in R diventa:
20 log R + 0.1 R = 65 - DT
si risolve in R tramite processi iterativi al P.C. ottenendo infine la tabella 3
| DT | 21.3 | 22.3 | 22.9 | 23.4 | 23.7 | 24 | 24.2 | 24.4 | 24.6 | 24.8 | 24.9 | 25 | 25.2 | 25.4 | 25.6 | 25.7 | 26 | 26.3 | 26.6 | 27.2 | R (Km) | 69 | 65 | 62 | 60 | 59 | 58 | 57 | 56 | 55.5 | 54.5 | 54 | 53.9 | 53.1 | 52.3 | 51.6 | 51.2 | 50.1 | 49 | 48 | 46 |
Si può osservare che l'ultima coppia di tabella coincide, come voluto, con la distanza computata per il sonar di riferimento: R = 46 Km per Pfa = 0.1 % e Priv. = 99%.
La soluzione del problema posto è ora mostrata in forma di grafico nella figura 1; in essa sono riportate le coppie di numeri di tabella 3 con la Priv. in ordinate, che decresce in funzione della distanza R in ascisse che da R = 46 Km s'incrementa verso i 70 Km; sempre per Pfa. = 0.1% costante.
In figura, tracciate in rosso, le coordinate della coppia di valori di partenza caratteristici del sonar di riferimento.
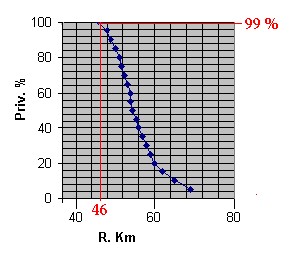figura 1 L'interpretazione della curva è la seguente:
Una volta fissata la soglia di falso allarme (Pfa. = 0.1%) la probabilità di rivelazione Priv, riportata in ordinate, decresce con l'aumentare della distanza R riportata in ascisse.
E' naturale che l'insieme delle computazioni e il grafico devono essere ripetuti per un sonar di riferimento diverso da quello di paragrafo 2.
4)Osservazioni sul significato dei calcoli
I risultati dei calcoli che hanno portato alla figura 1, anche se non hanno risvolti in situazioni operative reali, possono essere immaginati frutto di rilievi sul campo e così giustificati sulla base delle variabili riportate in precedenza:Se l'operatore addetto al sonar, dopo i calcoli di portata da svolgere secondo il paragrafo 2), imposta la soglia di rivelazione affinché la probabilità di falso allarme (Pfa.) sia quella messa a calcolo nel citato paragrafo: Pfa = 0.1 %; potrà osservare come la probabilità di rivelazione (Priv.) al livello del 99% con il bersaglio per R = 46 Km si riduca al solo 5% quando il bersaglio, allontanandosi raggiunge la distanza R = 69 Km.