SONAR-INFO-p268
Trasformazione delle caratteristiche di direttività con il "ConvGS" Dalle curve espresse con dati di tabella o da algoritmi trascendenti
alle funzioni gaussiane 1) Introduzione 2) L'idea dell'impiego della funzione gaussiana 3)La soluzione del problema dopo l'avvento dei P.C. 3.1)Soluzione in λ per caratteristiche di direttività esposte con tabelle 3.2)Soluzione in λ per caratteristiche di direttività esposte con funzioni trascendenti 4)Il software "ConvGS" per il calcolo e le presentazioni grafiche 4.1)Utilizzo del pannello di figura 7 per l'elaborazione di dati in numero discreto 4.2)Utilizzo del pannello di figura 8 per l'elaborazione della direttività di Stenzel 5)Le due versioni del programma di calcolo
La caratteristica di direttività di un sistema acustico indica come varia la sensibilità
di ricezione con il variare della direzione di provenienza dell'onda sonora.
Se la sensibilità è la massima possibile in una direzione e diminuisce molto rapidamente con il
variare di essa si dice che la base ricevente ha una buona direttività, cioè presenta una
direzione preferenziale d'ascolto.
La direttività di un gruppo di sensori, ottenuta sommando i contributi
di tensione generati dai singoli idrofoni opportunamente ritardati, è governata da leggi matematiche che
consentono di calcolare l'andamento della loro somma in funzione di diverse variabili quali:
le dimensioni, la frequenza, la larghezza della banda delle frequenze, l'angolo di provenienza
dell'onda acustica rispetto all'asse geometrico della base, il numero dei sensori che la costituiscono.
La caratteristica di direttività può essere determinata, secondo le necessità, o con algoritmi complessi
( si veda p39-par.6 ) o con di rilievi acustici sul campo mediante serie discreta di misure.
In entrambi i casi per un'elaborazione numerica è necessario che detta caratteristica venga espressa
con una funzione facilmente manipolabile con i mezzi dell'analisi matematica; vedremo quindi come determinare
questa particolare funzione.
Nella fase di studio delle problematiche connesse con il calcolo del minimo numero dei fasci preformati ( si veda p3 )
si è manifestata l'esigenza di trasformare una serie di rilievi strumentali ( espressi mediante una tabella ) in una funzione
matematica che fosse assimilabile all'andamento dei dati disponibili, almeno nei dintorni del massimo.
Visto il profilo della serie dei dati di tabella messi in forma di grafico si è individuato come buona parte del
profilo fosse simile alla funzione gaussiana, adatto quindi ad essere assimilato alla funzione:
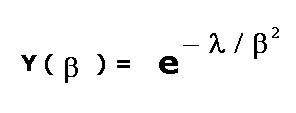1)
dove β è l'angolo che esprime la direzione del suono e λ il parametro distintivo di detta funzione.
Il grafico dell'approssimazione effettuata nell'ambito di p3 è mostrato in figura 1:
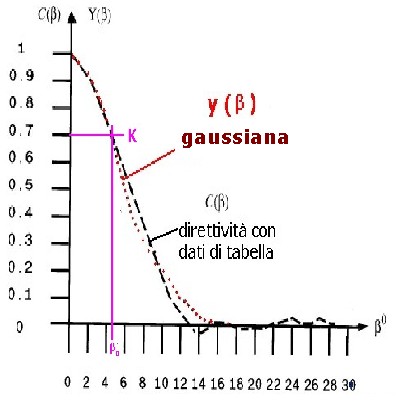figura 1
Nel caso specifico il valore di λ è stato calcolato, risolvendo il problema, secondo quanto illustrato in p3, affidandosi alla
sovrapposizione delle due curve nel punto a -3 dB sotto il massimo:
ovvero per λ= 4.5° e k = 0.7 risolvendo il problema in λ come segue:
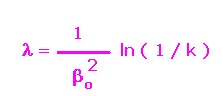2)
La soluzione in λ illustrata in precedenza, è frutto di un lavoro del 1990 quando i P.C. non erano ancora a disposizione
del diversi settori delle aziende che dovevano, invece, appoggiarsi al centro di calcolo naturalmente oberato da
altri impegni.
Il P.C. consente, per via analitica e grafica, la sovrapposizione della funzione gaussiana alla caratteristica
di direttività comunque disponibile, adattando al meglio il suo profilo nella parte più significativa della prima
(zona attorno al massimo) mediante variazioni precise di
λ che in tal modo risolve il problema con maggior aderenza al vero rispetto alla procedura riportata
nel paragrafo 2.
Supponiamo che a seguito di misure acustiche in mare sia stata rilevata, in una serie di operazioni successive, la
caratteristica di direttività di una base idrofonica e che i risultati dei rilievi siano riportati nella seguente
tabella TB1:
direz.°
amp.
amp.norm.
0
8.5
1.0
2
7.6
0.88
4
7.9
0.92
6
7.1
0.82
8
6.7
0.77
10
4.8
0.56
12
3.5
0.41
14
2.2
0.26
16
1
0.12
18
0
0
Nella prima colonna della tabella gli angoli relativi ai diversi puntamenti idrofonici; da 0° sull'asse
a 18° a passi di 2°.
Nella seconda colonna i valori di tensione rilevati, da 8.5 v a 0 v, nelle diverse direzioni di puntamento del sistema di misura.
Nella terza colonna gli stessi valori della colonna precedente trascritti in forma normalizzata; da 1 a 0.
La serie dei dati normalizzati è riportata nel grafico di figura 2:
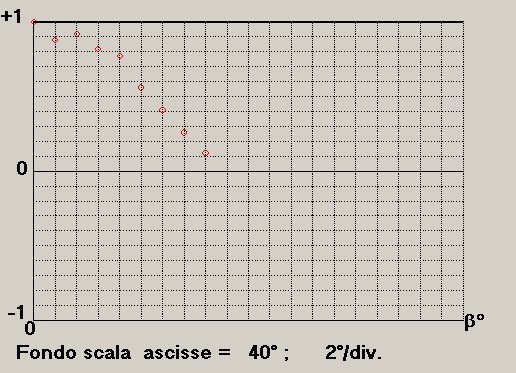figura 2
Come si nota da figura non tutti i valori seguono un profilo raccordabile ciò, supponendo ad esempio, per
incertezze sulle misure sul campo.
La figura 2 è ottenuta con apposita routine software che andremo a descrivere; con la stessa routine si potrà
tracciare la funzione gaussiana che meglio si adatta al profilo dei valori di figura 2 così come mostra la seguente
figura 3 che risolve il problema per λ = 0.007 :
figura 3
In questo caso, quindi, la funzione gaussiana sostitutiva della direttività misurata sul campo e:
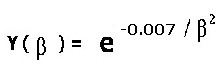3)
Supponiamo ora che la caratteristica di direttività di una base idrofonica sia stata calcolata secondo l'algoritmo
di Stenzel che riportiamo:
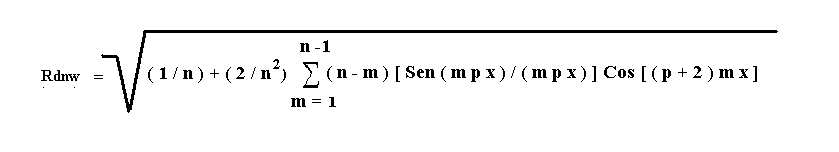4)
Dove:
n = numero degli idrofoni
d = L / ( n - 1 )
L = lunghezza della base in metri
X = ( 3.14 d f1 / c ) Sen (β)
f1 = frequenza inferiore della banda
f2 = frequenza superiore della banda
p = ( f2 - f1 ) / f1
Come si può intuire questa funzione non è manipolabile con le regole dell'analisi matematica, non resta quindi
che tracciarla in diagramma e, sulla curva ottenuta, adattare l'andamento di una adatta funzione gaussiana
sostitutiva.
Calcoliamo e tracciamo ora il grafico di Rdnw, secondo la 4), nell'ipotesi che siano stati assunti i seguenti dati
per la direttività:
n = numero degli idrofoni = 9
d = L / ( n - 1 ); dove L = 1m
f1 = frequenza inferiore della banda = 9000 Hz
f2 = frequenza superiore della banda = 12000 Hz
X = ( 3.14 d f1 / c ) Sen (β) ; dove c = velocità del suono in mare = 1530 mSec.
p = ( f2 - f1 ) / f1
Il risultato del calcolo, il grafico di Rdnw in funzione di β, è riportato in figura 4:
figura 4
La figura 4 è ottenuta con apposita routine software che andremo a descrivere; con la stessa routine si potrà
tracciare la funzione gaussiana che meglio si adatta al profilo dei valori di figura 4 così come mostra la seguente
figura 5 che risolve il problema per λ = 0.037 :
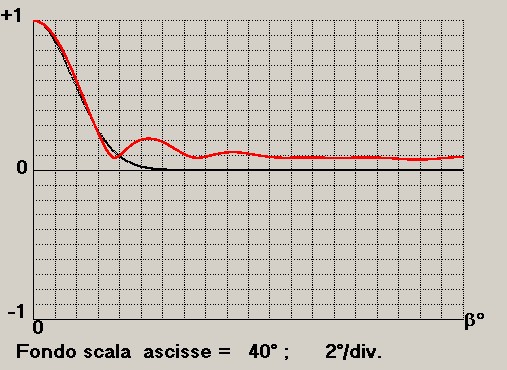figura 5
In questo caso, quindi, la funzione gaussiana sostitutiva della direttività calcolata è:
Y = exp (-0.037 β 2 )
Il ConvGS consente:
-la presentazione grafica delle caratteristiche di direttività definite per serie
discreta di valori
-il calcolo e la presentazione grafica delle caratteristiche di direttività definite attraverso una funzione
trascendente
-il calcolo ed il posizionamento grafico della funzione gaussiana sostitutiva delle direttività sopra menzionate
L'accesso al calcolatore avviene tramite il pannello principale mostrato in figura 6, da esso con i due pulsanti di comando si può
accedere alle due diverse modalità di calcolo:
-Elaborazione curva di direttività per serie discreta di dati.
-Elaborazione curva di direttività di funzione trascendente.
figura 6
Il pannello di calcolo per la prima elaborazione dati è mostrato in figura 7:
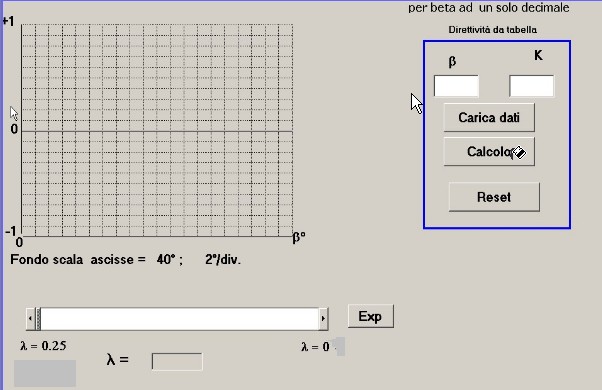figura 7
Il pannello di calcolo per la seconda elaborazione dati è mostrato in figura 8:
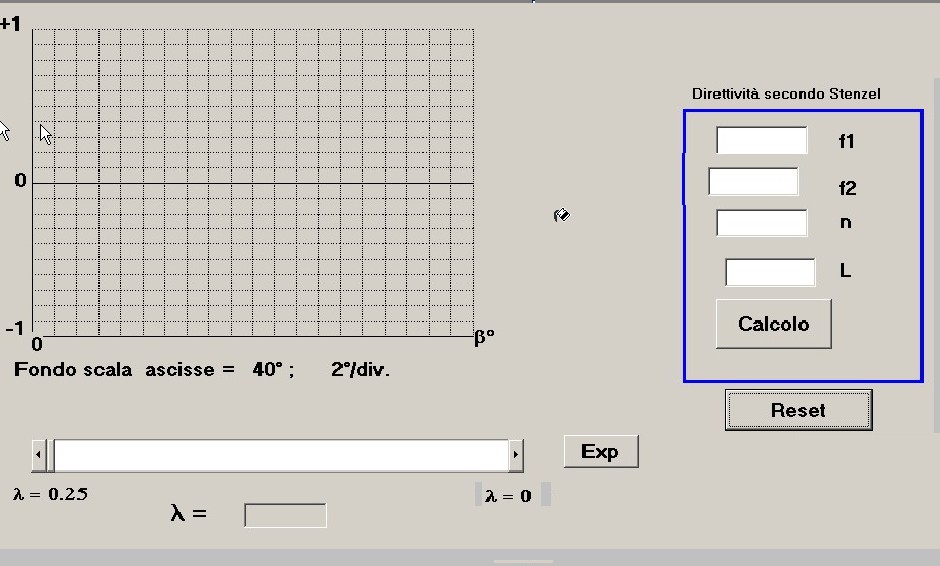figura 8
Vediamo ora come utilizzare il pannello di figura 7 :
Nel riquadro in alto a destra si digitano le coppie di valori con riferimento a serie di dati misurati a mare
, ad esempio la serie mostrata nella tabella TB1, dove la
prima coppia normalizzata è β = 0° amp.norm K = 1, la seconda β = 2° amp.norm K = 0.88 ecc..
Dopo l'inserimento della prima coppia di valori 0; 1 si preme "Carica dati" quindi "Calcolo" e si ha la
presentazione del primo punto sul tracciato cartesiano a sinistra così come mostra figura 9:
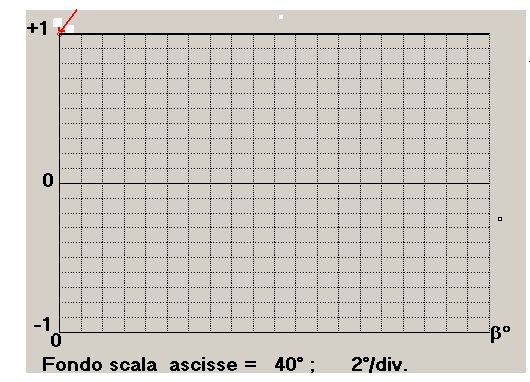figura 9
Dopo l'inserimento della seconda coppia di valori 2; 0.88 si preme "Carica dati" quindi "Calcolo" e si ha la
presentazione del secondo punto sul tracciato cartesiano a sinistra così come mostra figura 10:
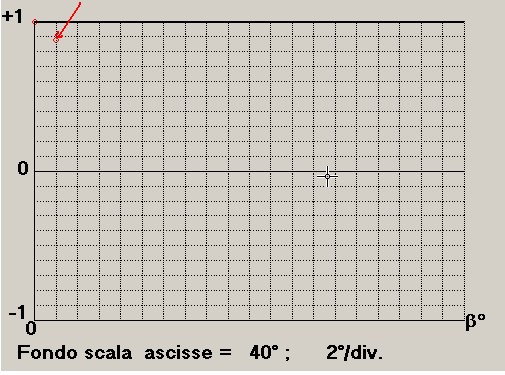figura 10
e così procedendo per tutte le altre coppie di TAB1 si ottiene la schermata già mostrata in figura 2 che riportiamo:
figura 2
A questo punto dobbiamo prendere in considerazione la slitta nella parte inferiore del pannello di figura 7 e l'indicatore
di λ sottostante, con essi si
regola il valore di λ, compreso tra il massimo di 0.25 ed il minimo 0, affinché dopo la pressione del pulsante
"exp" si abbia il profilo della funzione gaussiana meglio rispondente al profilo della direttività; naturalmente
l'operazione di regolazione del λ deve essere ripetuta fino al raggiungimento dell'obiettivo.
Si osservi che:
a) Spostando la slitta a destra il profilo della gaussiana diventa più ampio.
b) La pressione del pulsante "exp" può essere sostituita con vantaggio dalla pressione delle frecce destra/sinistra
della slitta
Il risultato dell'operazione riferito alla direttività di figura 2 è riportato in figura 3 che riportiamo:
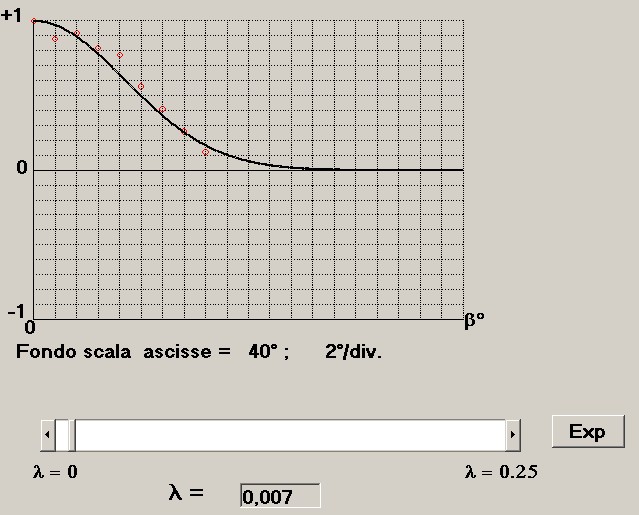figura 3
Il valore di λ della funzione gaussiana sostitutiva è quindi λ = 0.007: ovvero:
Y = exp (-0.007 β 2 )
Per cancellare tutti i dati inseriti e i grafici si deve agire sul pulsante "Reset"
Come utilizzare il pannello di figura 8 :
Nel riquadro in alto a destra si digitano i 4 dati che concorrono al calcolo della direttività di una base idrofonica
secondo l'algoritmo di Stenzel illustrato nella 4); quelli ad esempio già esposti nel paragrafo 3.2:
f1 = frequenza inferiore della banda = 9000 Hz
f2 = frequenza superiore della banda = 12000 Hz
n = numero degli idrofoni = 9
L = lunghezza della base = 1m
di seguito si preme il pulsante "calcolo" e si ottiene la curva voluta così come già mostrato in figura 4
che riportiamo:
figura 4
Eventuali errori di digitazione dei dati possono essere eliminati con il pulsante "reset" che cancella tutti i dati già
inseriti.
Dobbiamo ora, in modo simile al paragrafo precedente, prendere in considerazione la slitta nella parte inferiore
del pannello di figura 8 e l'indicatore di λ sottostante, con essi si
regola il valore di λ, compreso tra il massimo di 0.25 ed il minimo 0, affinché dopo la pressione del pulsante
"exp" si abbia il profilo della funzione gaussiana meglio rispondente al profilo della direttività; naturalmente
l'operazione di regolazione del λ deve essere ripetuta fino al raggiungimento dell'obiettivo.
Si osservi che:
a) Spostando la slitta a destra il profilo della gaussiana diventa più ampio.
b) La pressione del pulsante "exp" può essere sostituita con vantaggio dalla pressione delle frecce destra/sinistra
della slitta
Il risultato dell'operazione riferito alla direttività di figura 4 è riportato in figura 5 che riportiamo:
figura 5
Il valore di λ della funzione gaussiana sostitutiva è quindi λ = 0.037: ovvero:
Y = exp (-0.037 β 2 )
Il programma di calcolo è proposto in due versioni; con file eseguibile e con routine sorgente in VB6:
- Il primo disponibile su file exe in ConvGS
- Il secondo su file zip in: GS17.zip
Con il file exe si può procedere immediatamente ai calcoli; con il file zip si possono modificare le variabili
e le formule di calcolo secondo diverse impostazioni concettuali.
Home