SONAR-INFO-p272
Sulle portate di scoperta in passivo dipendenti dalla banda di ricezione del sonar.
1) Generalità
Il problema relativo al calcolo delle portate di scoperta di un sonar, in modalità passiva, dipendenti dalle variazioni della banda di ricezione non è mai stato trattato nelle pagine di questo sito.In questa pagina affronteremo il problema, come esercizio strettamente speculativo, facendo ricorso al calcolatore SONARMATH, illustrato a pagina p6, con il quale risolvere in breve tempo la notevole mole di calcolo necessaria alla soluzione reiterata del sistema trascendente che caratterizza il funzionamento del sonar passivo.
2)Il sistema trascendente caratteristico del sonar passivo
Il sistema in oggetto, illustrato in p42, è riportato di seguito per il presente sviluppo:
le due equazioni dipendono dalla frequenza centrale di lavoro, fo, e dalla banda BW del ricevitore che ha fo come media geometrica dei suoi estremi; vediamone i dettagli addendo per addendo:
-Prima equazione
Il coefficiente "a" del terzo addendo della prima equazione dipende da fo secondo la funzione:

-Seconda equazione:
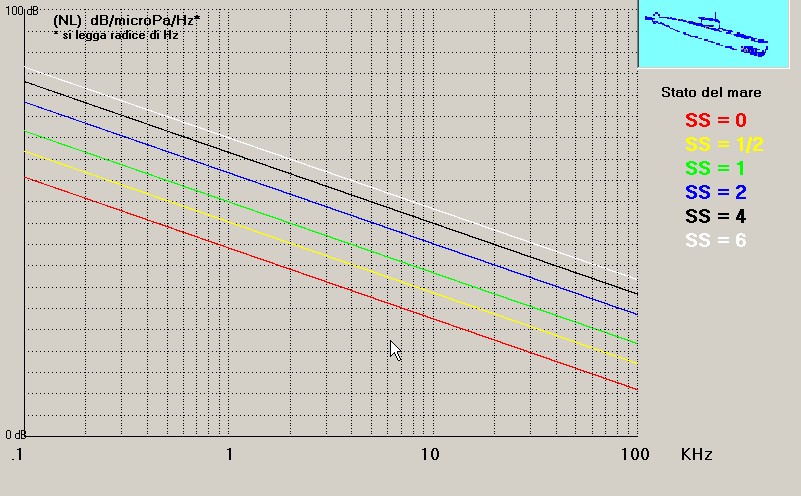
Il termine SL in dB ( livello di rumore emesso dalla sorgente ) dipende da fo secondo l'andamento delle curve sotto riportate:

Il termine DI in dB ( guadagno della base ricevente ) dipende da fo secondo 20 Log(G) dove G è dato dall'equazione seguente:
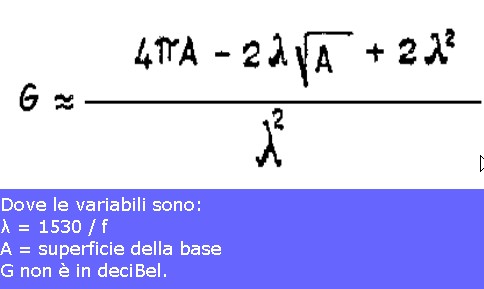
Il termine NL in dB ( livello del rumore del mare ) dipende da fo secondo l'andamento delle curve sotto tracciate:
Il termine DT in dB ( soglia di rivelazione ) dipende da BW secondo l'andamento della funzione:

Il termine 10 Log BW è l'unico addendo che dipende direttamente soltanto da BW.
Dall'esame del sistema trascendente si evince quindi che in esso compaiono, sia la frequenza centrale di ricezione del sonar indicata con fo, sia la larghezza di banda BW.
Se la banda BW è definita tra f1 (frequenza inferiore) ed f2 ( frequenza superiore ) dovranno essere sempre verificate le due condizioni:
BW = f2 - f1 ( differenza tra la frequenza superiore e la frequenza inferiore )
fo = √ ( f1 x f2 ) ( media geometrica tra la frequenza superiore e la frequenza inferiore ).
Da quanto sopra si può comprendere che una volta determinata, in fase di progetto del sonar, la frequenza centrale della bada di ricezione, ad esempio fo = 5000 Hz, qualsiasi banda BW = f2' - f2' potrà essere selezionata, a comando dell'operatore, purché sussista sempre la relazione:
√ ( f1' x f2' ) = 5000 Hz
3)Calcolo della portata di un sonar di riferimento
Per la prosecuzione del nostro lavoro è utile il calcolo della portata di un sonar, che riterremo di riferimento, sul quale determinare le variazioni della portata R in funzione della variazione delle larghezza di banda BW.Per la soluzione del sistema trascendente in R si utilizza il calcolatore veloce SONARMATH ( nella sezione dedicata al calcolo della portata dei sonar passivi) inserendo, a titolo d'esempio, la sequenza delle seguenti variabili:
f1 = 2000 Hz
f2 = 6000 Hz
SL = 112 dB
DI = 24 dB
NL = 48 dB
RC = 1 Sec.
d = 2
Si osservi che in questo caso la frequenza centrale della banda è fo = √ ( 2000 x 6000 ) = 3464 Hz e la larghezza di banda è f2-f1 = 4000 Hz.
Il calcolo con SONARMATH, una volta digitate le variabili sopra indicate, porta al risultato mostrato di seguito nel pannello operativo della sezione prescelta dall'operatore:
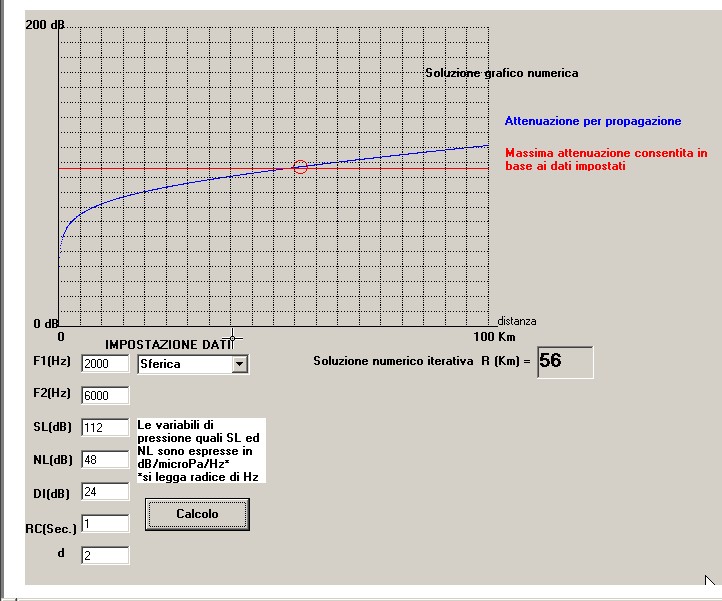
Come si vede la portata di scoperta R risulta, sia nel grafico che nella casella del calcolo numerico iterativo pari a 56 Km.
Con i risultati che caratterizzano il sonar di riferimento possiamo procedere alla determinazione di una serie di valori di BW che, soddisfacendo sempre la relazione √ ( f1' x f2' ) = 3464 Hz, consentano di determinare una relazione tra portata e larghezza di banda del sonar : la funzione R = f(BW).
4)Calcolo per punti della funzione R = f(BW)
Il calcolo di R = f(BW) si esegue per un numero discreto di valori di BW che abbiano come frequenze superiori valori compresi, ad esempio, tra f2 = 4000 Hz e f2 = 20000 Hz così come mostra la seguente tabella 1: tab1
tab1 Ora essendo il valore del centro banda del sonar di riferimento pari a fo = 3464 Hz a ciascuna frequenza superiore fmax (f2) della banda indicata in colonna dovrà corrispondere la frequenza inferiore fmin (f1) secondo la relazione:
f1 = 3464 2 / f2
che garantisce fo = 3464 come nel sonar preso a modello, quindi la nuova tabella a due colonne delle corrispondenze tab.2:
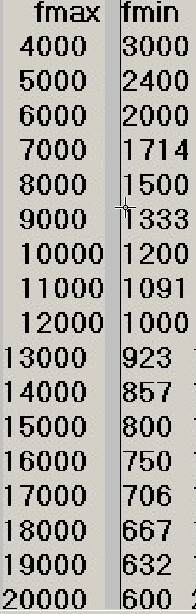 tab2
tab2 Una terza tabella mostra le relazioni tra gli estremi di banda fmax e fmin, le larghezze di banda BW corrispondenti :
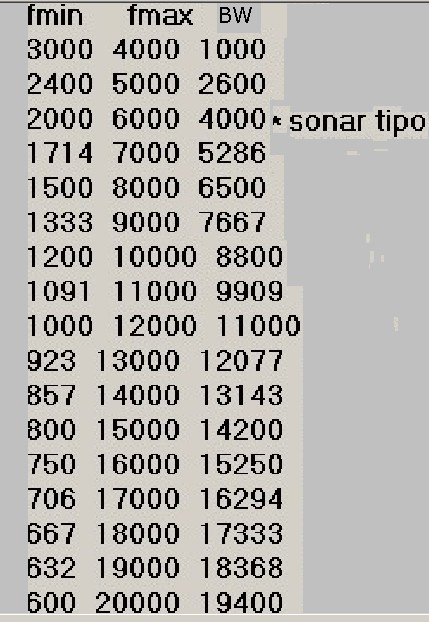 tab3
tab3 Con i dati della tabella 2 si eseguono, con la sezione già menzionata del SONARMATH, i calcoli di portata assumendo per tutte le altre variabili gli stessi valori del sonar di riferimento; per ciascuna delle 17 bande ottenendo infine la funzione per punti R = f(BW) così come mostra la quarta tabella:
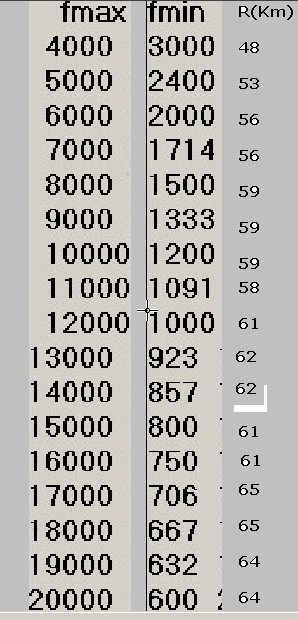 tab4
tab4 Dalla tabella 4, infine, si ottiene il diagramma che mostra l'andamento della R = f(BW); in ascisse i valori della larghezza di banda espressi in Hz, relativi alle 17 bande, in ordinate i valori di portata R espressi in Km:
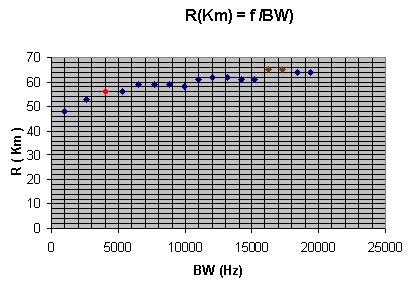
Nel diagramma il punto rosso si riferisce alla banda del sonar di riferimento "4000 Hz" , per la quale R = 56 Km, mentre i due punti viola rappresentano il valore di banda che porta il sonar di riferimento, se predisposto in banda 700-17000, ad avere una portata di 64 Km contro i 56 Km della banda originale.