SONAR-INFO-p276

1) Generalità
Il calcolatore PSRP, progettato per risolvere rapidamente il problema relativo al calcolo della previsione di portata di un sonar passivo, è stato illustrato in p2018a senza alcun dettaglio in merito alla filosofia operativa che, per qualche lettore, potrebbe essere d'utilità.Come illustrato nella pagina citata il PSRP risolve il sistema trascendente in R:

dopo l'inserzione delle variabili:
-Del SONAR:
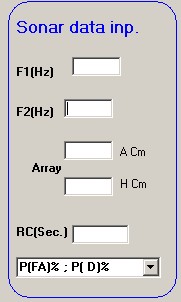
-Dell'ambiente marino:
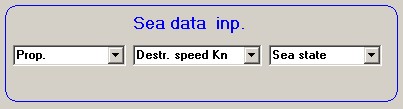
Vediamo di seguito con quale procedura i dati inseriti portano al calcolo di R.
2): Le variabili del SONAR
2.1)La coppia delle frequenze che definiscono la banda del ricevitore
-Indicata con F1 la frequenza inferiore della banda-Indicata con F2 la frequenza superiore della banda
si calcolano come primo passo:
La larghezza di banda: BW = F2 - F1
La frequenza media geometrica della banda : Fo =√ (F1 x F2)
2.2) Il guadagno di direttività della base ricevente "DI"
-Indicata con "a" la larghezza della base, con "h" l'altezza si calcola la superficie A = "a" x "h"-Utilizzando la frequenza Fo dai calcoli precedenti si calcola la lunghezza d'onda λ = C / fo
- Il guadagno della base in forma non logaritmica è dato da :
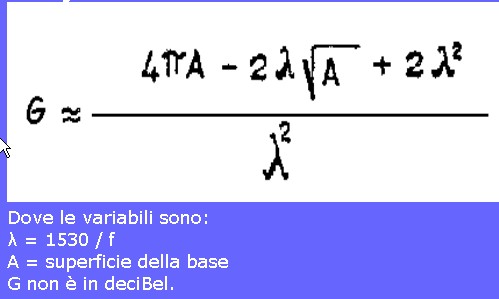
Il valore del DI riportato nel sistema iniziale è calcolato con:
DI = 10 Log G.
2.3 La costante di tempo "RC"
- Il valore di "RC", in secondi, stabilito al momento dall'operatore al sonar, caratterizza la costante di tempo d'integrazione da assegnare al sistema di rivelazione in correlazione in funzione delle condizioni di scoperta del bersaglio.2.4) Il valore "DT" da computare secondo la scelta della coppia P(FA); P(D)
La coppia probabilistica P(FA): P(D), selezionabile dall'operatore secondo la tabella:"P(FA)=1 ; P(D)=90" d = 13
"P(FA)=2 ; P(D)=80" d = 8.4
"P(FA)=5 ; P(D)=70" d = 4.7
"P(FA)=10 ; P(D)=60" d = 2.3
"P(FA)=20 ; P(D)=50" d = 0.7
"P(FA)=30 ; P(D)=40" d = 0.07
consente di fissare il valore del parametro "d" con il quale secondo l'equazione:

si determina la soglia
di rivelazione "DT" .
Come si vede il valore del "DT" è calcolato, oltre che con la variabile "d", anche con la variabile "BW" determinata
in precedenza e con il valore di "RC" di cui al punto 2.3).
3): Le variabili nell'ambiente (il mare)
3.1 L'impostazione del tipo di propagazione normale - Il tipo di propagazione, stabilito al momento dall'operatore al sonar, determina il valore del TL secondo la selezione di una delle due equazioni:Per propagazione "Sferica" TL = 60 + 20 Log R + ar
Per propagazione "Sferico-cilindrica" TL = 60 + 10 Log R + ar
La soluzione delle equazioni è legata al calcolo preventivo di "a" secondo l'espressione:

dove fo = Fo è la frequenza media geometrica della banda calcolata al punto 2.1).
3.2 L'impostazione della velocità del bersaglio
L'operatore può selezionare la velocità secondo la tabella:
"DS 10 Kn" livdB = 127.5 - Y
"DS 15 Kn" livdB = 138 - Y
"DS 20 Kn" livdB = 145.4 - Y
"DS 25 Kn" livdB = 151.4 - Y
"DS 30 Kn" livdB = 156.2 - Y
dove:
livdB è il valore di "SL"
db = 6.67
k = db / (20 * Log(2) )
Y = 20 * Log((Fo) ^ k)
"livdB" rappresenta la legge di variazione dell'intenssità del rumore del bersaglio, in funzione della frequenza Fo e della velocità "DS", emessa dal bersaglio secondo l'andamento delle curve mostrate sotto:
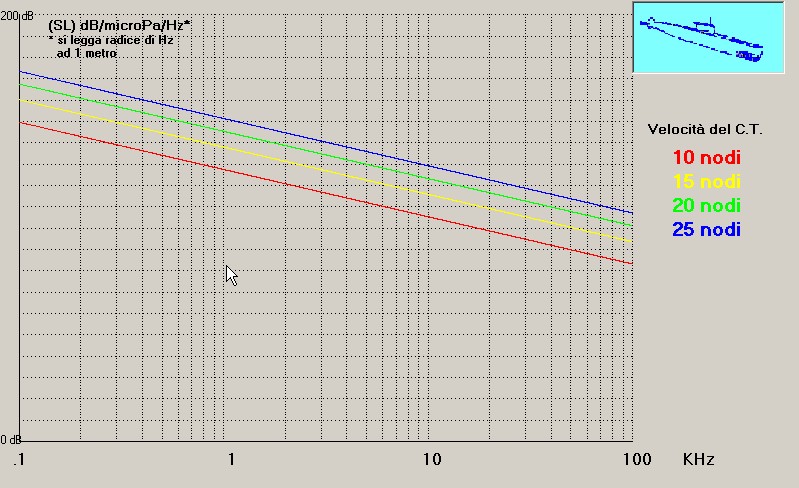
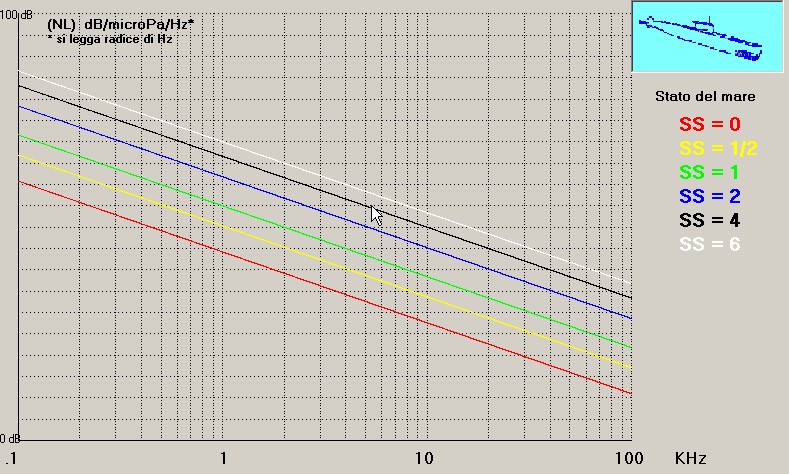
3.3 Il livello del rumore del mare
espresso in dB/ μPa/Hz, ed è funzione dell'ampiezza delle onde, espresso con il simbolo relativo allo stato del mare "SS"".
L'operatore può selezionare il valore di "SS" secondo la tabella:
"SS = 0" livdbj = 55 - Yj - 10.8
"SS = 1/2" livdbj = 55 - Yj - 4.7
"SS = 1" livdbj = 55 - Yj + 0
"SS = 2" livdbj = 55 - Yj + 6.8
"SS = 4" livdbj = 55 - Yj + 11.6
"SS = 6" livdbj = 55 - Yj + 15
dove:
livdbj è il valore di "NL"
xj = Fo / 1000
dbj = 5
kj = dbj / (20 * Log(2) )
Yj = 20 * Log((xj) ^ kj)
"livdBj" rappresenta la legge di variazione dell'intensità del rumore del mare, in funzione della frequenza Fo e dello stato "SS" secondo l'andamento delle curve mostrate sotto:
4) Soluzione del sistema trascendente
Con la variabili determinate in 2) e 3) procediamo infine alla soluzione del sistema:
:

4.1) Soluzione grafica
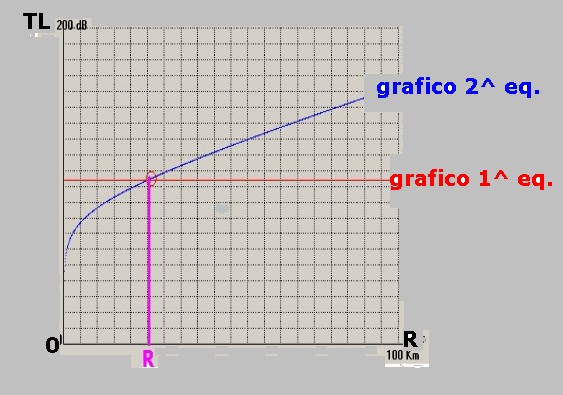
Se in una coppia di assi cartesiani, ascissa in R e ordinata in TL, tracciamo i grafici relativi alle due equazioni
del sistema abbiamo:
-Il valore del TL della prima equazione è indipendente da R e percio sarà una retta parallela all'asse delle ascisse.
-Il valore del TL della seconda equazione è funzione di R e sarà quindi rappresentato da una curva, il punto
d'intersezione tra i due grafici avrà come ascissa il valore cercato di "R" che risolve il nostro problema così
come mostra il tracciato che segue:
4.2) Soluzione numerica con processo iterativo
La soluzione al titolo è fattibile facendo girare il seguente ciclo for:
'hhh = 20 per prop Sferica
'hhh = 10 per prop Sferico-cilindrica
For R = 0.1 To 200 Step 0.1
TL = SL + DI - NL - DT + Bw
TLP = (60 + hhh * Log(R) + a * R)
If Int(TLP) = Int(TL) Then distanza = R
If Int(TLP) = Int(TL) Then perdita = TLP
Next
Print distanza