SONAR-INFO-p282
SOFAR 1) Introduzione 2) Condizioni per il verificarsi del fenomeno SOFAR 3)L'influenza dell'inclinazione dei raggi acustici 4)L'influenza della frequenza nel canale SOFAR 5)Cenni sui trasduttori per l'emissione nel canale SOFAR
-il canale di propagazione del suono a grande distanza-
-considerazioni numeriche-
Nell'ambito di questo sito sono stati illustrati diversi modi di propagazione del suono in mare, sia
in condizioni "normali", sia in condizioni dette "anomale" ; in p252 si è accennato, in particolare,
al fenomeno della canalizzazione del suono esaminando l'argomento senza alcun riscontro numerico, in
questa pagina tratteremo il fenomeno , nominato in gergo "SOFAR" (Sound Fixing And Ranging channel), alla
luce di alcune considerazioni di carattere matematico.
In ambienti marini oceanici, alle medie latitudini e a profondità comprese tra 800-1000 metri la velocità
del suono raggiunge i valori più bassi a causa delle basse temperature dell'acqua; in queste condizioni i
raggi sonori emessi da una sorgente acustica vengono deviati, ondulando verso l'alto e verso il basso,
in una alternanza di rifrazioni verso la quota dove è minima la velocità del suono, si
da creare , per particolari inclinazioni dei raggi, un canale acustico in grado di far giungere il suono della sorgente a grandissime distanze.
Un'idea del fenomeno è data dalla figura 1 nella quale, a sinistra, è riportato il grafico della velocità del suono
in funzione della profondità che mostra come detta velocità raggiunga i minimi valori ad una profondità di circa 1000 metri.
La conseguenza di questo comportamento della velocità del suono è mostrata nella
parte destra di figura 1 nella quale sono tracciati i raggi acustici emessi dalla sorgente che ondulando in
alto e in basso allontanandosi dalla stessa per centinaia di chilometri.
figura 1
Nella figura è tracciato, grazie al fenomeno SOFAR, una sorta di canale acustico che trasferisce le onde sonore
della sorgente verso il ricevitore posto a oltre 200 Km (nb. il diagramma della parte destra è deformato dato
che, a parità di lunghezza delle coordinate le ascisse riportano distanze dell'ordine di centinaia di Km mentre le ordinate dell'ordine di alcuni chilometri) .
Il fenomeno SOFAR, generalmente, si verifica quando l'inclinazione massima dei raggi acustici è compresa, nel piano verticale, tra
+/- 12° rispetto all'asse orizzontale del generatore; se l'angolo di emissione supera tali valori molta energia
acustica viene a colpire sia la superficie del mare, sia il fondo come mostra la figura 2:
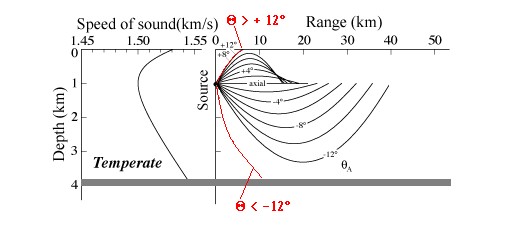figura 2
Le onde che sono emesse sotto i +/-12° sono rifratte, in alto ed in basso , verso l'asse orizzontale della sorgente,
senza incidere ne sulla superficie del mare ne sul fondo, subiscono attenuazione sia per assorbimento che per
divergenza cilindrica.
Le onde che sono emesse oltre i +/-12° colpiscono sia il fondo che la superficie disperdendo parte dell'energia
sonora emessa.
Le onde che colpiscono la superficie non sono facilmente rivelabili.
Come accennato al paragrafo precedente i raggi sonori, che percorrono il canale SOFAR, subiscono i fenomeni
di attenuazione sia per divergenza cilindrica sia per assorbimento.
L'attenuazione per divergenza cilindrica TLc ( espressa dB ) è, come noto, dipendente dalla distanza R ed è indipendente dalla frequenza F
e risponde alla legge:
TLc = 30 + 10 Log (Rkm) ----1).
L'attenuazione per assorbimento, att ( espressa in dB ) dipende invece sia dalla frequenza sia dalla distanza come sotto indicato
nell'espressione di att. dove R è espresso in Km e la frequenza in KHz.
---- 2)
Un semplice esempio per avere un'idea delle attenuazioni nel canale SOFAR è di seguito mostrato per una
distanza sorgente-ricevitore pari a 100 Km:
L'attenuazione per divergenza cilindrica si ottiene con la 1):
TLc = 30 + 10 Log 100 = 50 dB
L'attenuazione per assorbimento, calcolabile con la 2), richiede di fissare un valore della frequenza del
segnale acustico emesso; per vedere come gioca il valore della frequenza nel fenomeno calcoliamo con la 2)
tre valori diversi dì attenuazione; per F = 100 Hz, F = 1000 Hz e F = 10000 Hz e per R = 100 Km si ha:
per F = 100 Hz : att = 1.6 dB
per F = 1000 Hz : att = 6 dB
per F = 10000 Hz : att = 110 dB
Tenendo conto della 1) avremo tre valori globali di attenuazione (ATT) pari a :
per F = 100 Hz : ATT = 50 dB + 1.6 dB = 51.6 dB
per F = 1000 Hz : ATT = 50 dB + 6 dB = 56 dB
per F = 10000 Hz : ATT = 50 dB + 110 dB = 160 dB
Come si vede la differenza di attenuazione è nettamente a favore delle frequenze basse per le quali
si potrebbe sempre protendere, questa scelta non è però facilmente attuabile date le dimensioni che i
trasduttori di emissione dovrebbero avere per assicurare un'ampiezza del lobo di direttività
verticale di 24° (12° verso l'alto e 12° verso il basso);
di questo problema accenniamo nel paragrafo seguente.
Per chiudere questa pagina esamineremo, a solo scopo illustrativo, come dovrebbero variare le dimensioni di un
trasduttore d'emissione per completare l'analisi dei dati indicati nel paragrafo 4).
E' noto come le dimensioni dei trasduttori siano dipendenti sia dalla frequenza di lavoro, sia
dall'ampiezza del lobo di direttività voluto; nel caso numerico di paragrafo 4) le frequenze
messe a calcolo sono:
F1 = 100 Hz
F2 = 1000 Hz
F3 = 10000 Hz
L'ampiezza del lobo di direttività verticale deve essere: Θ = 24°
La lunghezza del trasduttore, ipotizzando una base lineare posta in senso verticale,
calcolata con il calcolatore SONARMATH di p6 sarà:
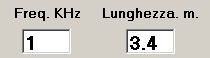
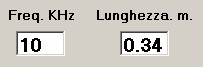
I dati sopra esposti indicano che per il canale SOFAR un ragionevole compromesso deve essere fatto per
conciliare la scelta delle frequenze che consentono perdite di assorbimento più basse con la fattibilità dimensionale del
trasduttore d'emissione.