SONAR-INFO-p286
Correlatori e rivelatori d'energia
*la scoperta dei segnali mascherati dai disturbi*
- Esposizione per immagini e poca matematica -
1) Generalità
L'inizio di questa pagina tratta, con immagini, delle caratteristiche dei segnali e dei rumori nell'ambiente marino, di seguito si esamina, a grandi linee, il funzionamento del rivelatore d'energia che sarà preso come paragone per la successiva esposizione del funzionamento del correlatore, di quest'ultimo si evidenzieranno le caratteristiche salienti sia in termini di discriminazione dei segnali coperti dal rumore, sia dell'effetto che il disturbo provoca sulla capacità di rivelazione.
Ricordando che i processi di correlazione possono essere implementati sia con routine software sia con insiemi di componenti elettronici sparsi, si tratti di singoli correlatori o di correlatori multipli, vediamo di sviluppare questo lavoro secondo la seconda strada per un più semplice comprensione nella speranza che possa essere d'aiuto e d'incentivo per affrontare la problematica ad un livello più elevato.
2)Come si presentano i segnali idrofonici ed i segnali d'uscita dei correlatori.
I segnali idrofonici dei quali trattiamo sono sempre generati dai gruppi pari di sensori idrofonici ( 2; 4; 6; 8; ecc.. ) quali ad esempio quelli del sonar IP70 dei quali un esemplare è mostrato in figura 1:
figura 1 Le tensioni d'uscita di una coppia d'idrofoni nel caso in cui questi siano colpiti dal solo rumore del mare è mostrata per uno dei due, su oscilloscopio, in figura 2
figura 2 Se nell'ambiente marino è presente anche il rumore generato da una nave, e se questo è sensibilmente elevato rispetto al rumore del mare, il segnali d'uscita della coppia d'idrofoni mostreranno l'insieme del rumore del mare nel quale emerge il rumore del bersaglio così come mostra, per uno dei due idrofoni, la figura 3 :
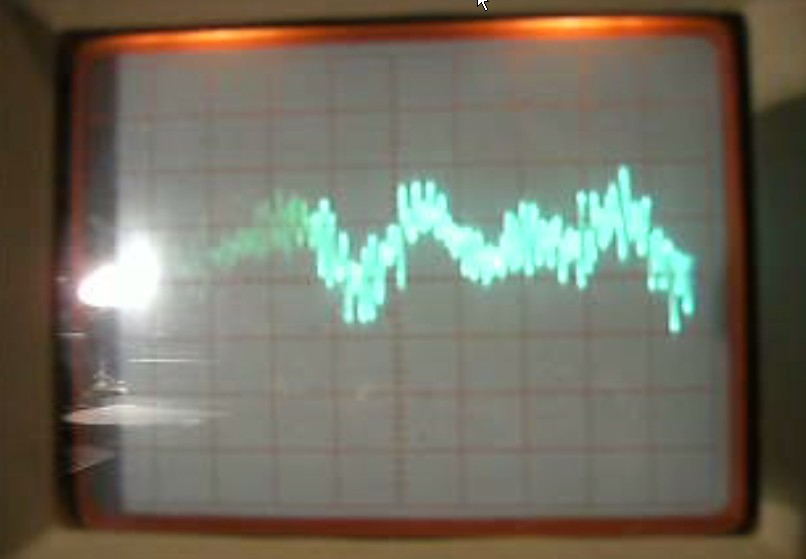figura 3 Se la situazione ambientale porta alla condizione di figura 3 nessun processo di correlazione è necessario dato che la presenza del segnale, essendo il suo livello elevato, è manifestamente evidenziata rispetto al rumore ambiente.
L'implementazione dei processi di correlazione, per evidenziare piccoli segnali mascherati dal rumore del mare è d'obbligo quando, nonostante la presenza di un segnale, all'uscita dei sensori idrofonici si osserva ancora l'immagine mostrata in figura 2; non si può quindi affermare, quando l'immagine oscilloscopica è quella indicata, ne la presenza ne l'assenza di segnale, confondendosi quest'ultimo nell'insieme della tensione di rumore.
In tal caso per scoprire se il segnale è presente o assente si deve operare con un sistema di correlazione; l'utilizzo di tale mezzo nel caso di presenza di segnale è illustrato da fotografie rilevate su sistemi sperimentali:
La fotografia di figura 4 mostra l'uscita di un sistema di correlazione multiplo quando il rumore del mare è presente e il segnale è assente.
La fotografia di figura 5 mostra l'uscita menzionata quando il segnale è presente a livello di 1/5 rispetto al rumore ambiente.
figura 4 
figura 5 Si deve osservare che nelle due fotografie le tracce luminose ondulanti non sono quelle all'uscita degli idrofoni illustrate in figura 2 ma prodotti spuri generati dai correlatori.
Con questi metodi si può scoprire, sotto particolari condizioni, segnali a livello di 1/10 rispetto al rumore ambiente anch'esso presente.
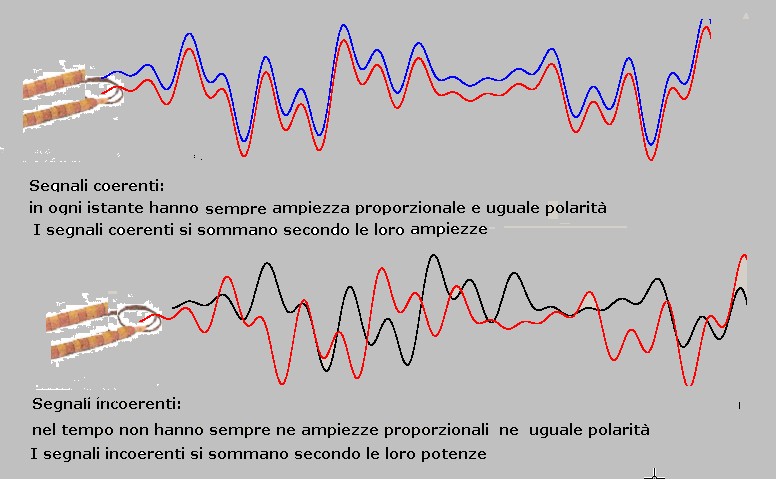
Dato che nel prosieguo della esposizione si farà cenno a segnali "coerenti" ed "incoerenti" la figura seguente mostra graficamente la differenza tra i due:
3) Il rivelatore d'energia per la scoperta del segnale in mezzo al disturbo
Prima di esaminare per via numerica i sistemi di correlazione è utile, per confronti successivi, analizzare il
processo di rivelazione d'energia.
Alle origini delle tecniche per la scoperta dei bersagli in mezzo al rumore del mare il dispositivo che
andava per la maggiore era il "rivelatore d'energia"; con questo circuito si confrontava il suo livello
d'uscita in presenza del solo rumore del mare, e di seguito, con la presenza di rumore più il segnale.
Il rivelatore di energia è costituito da due sezioni; I^ "sezione: rivelatore" ; II^ "sezione: sommatore".
Lo schema elettrico della prima sezione è riportato in figura 6:
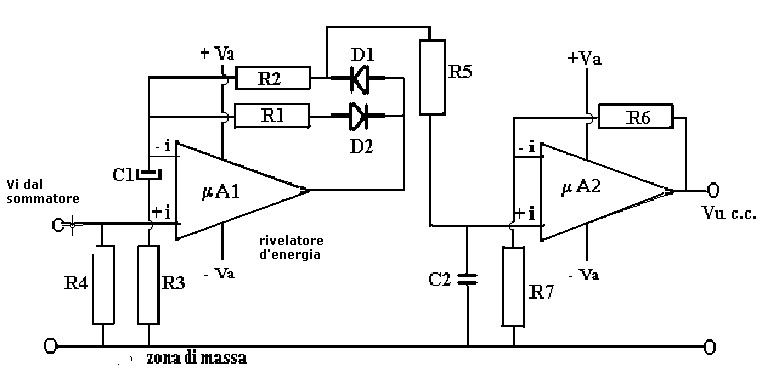figura 6
L'uscita del rivelatore è una tensione continua, Vurcc, di ampiezza proporzionale al segnale alternato d'ingresso,
la Vurcc presenta un'ondulazione perturbante detta "varianza" la cui ampiezza
dipende dal valore del prodotto ( R5 x C2 )espresso in secondi ( costante di tempo d'integrazione ).
Se il valore di ( R5 x C2 ) cresce la varianza diminuisce ma il rivelatore ha una riduzione della velocità
di risposta ;
un giusto compromesso và scelto in base delle necessità operative.
Dato che ad ogni sistema di scoperta sono previste sempre coppie di idrofoni le tensioni d'uscita di questi , per essere
applicate alla I^ sezione, dovranno essere sommate tra loro; la somma è eseguita nella II^ sezione secondo lo schema elettrico
riportato in figura 7:
figura 7
Per comprendere il comportamento di tali circuiti facciamo un semplice esempio numerico:
Supponiamo che i due idrofoni di figura 7 captino soltanto i rumori del mare (N1; N2) e che la loro uscita, in termini di
tensione sia :
N1 = 10 mV eff. per un idrofono ed N2 = 10 mV eff. per l'altro.
Le due tensioni non saranno tra loro coerenti perché generate da rumori del mare incidenti su idrofoni
disposti volutamente a distanza calibrata tra
loro.
Le due tensioni incoerenti, inviate al sommatore, si addizioneranno secondo le loro potenze e il risultato dell'operazione sarà:
SommaN = √ ( N12 + N22 ) = √ ( 102 + 102 ) = 14,1 mVeff.
Se fissiamo ora per il rivelatore un guadagno G = Vurcc/Veff. = 710 la SommaN, applicata ad esso, produrrà all'uscita
una tensione continua Vurcc = 710 x 14.1 mVeff = 10 Vcc.
Supponiamo ora che assieme al rumore incoerente che colpisce gli idrofoni siano presenti due segnali
di ampiezza metà rispetto al rumore per un rapporto segnale disturbo pari a ( S/N ) = 0.5 ;
S1 = 5 mVeff. ed S2 = 5 mVeff che provenendo dalla stessa sorgente siano coerenti e come tali si sommino
secondo le loro ampiezze:
SommaS = S1 + S2 = 5 + 5 = 10 mV eff.
SommaS non è però coerente con SommaN pertanto si addizionerà a quest'ultima secondo le potenze quindi la tensione totale
d'uscita del sommatore sarà:
SommaT = √ ( SommaS2 + SommaN2 ) =
√ ( 102 + 14,12 ) = 17.28 mVeff e di conseguenza Vurcc sarà :
Vurcc = 710 x 17.28 mVeff. = 12.27 Vcc
con un incremento, rispetto alla presenza di solo rumore, di 12.27 Vcc. - 10 Vcc. = 2.27 Vcc.
Questo incremento, apprezzabile, denuncia la presenza del segnale quando questo è, come nell'esempio,
pari alla metà del rumore.
Se il segnale invece di essere la metà del rumore ne è, ad esempio, 1/5 pari ad un rapporto
tra segnale e disturbo ( S / N )= 0.2
avremo una diversa situazione come mostrano le seguenti operazioni:
S1 = 2 mV eff. ; S2 = 2 mV eff. quindi SommaS = 4 mV eff.
perciò :
SommaT = √ ( SommaS2 + SommaN2 ) =
√ ( 42 + 14,12 ) = 14.6 mVeff ;
per conseguenza Vurcc sarà: Vurcc = 710 x SommaT = 710 x 14.6 mVeff. = 10.4 Vcc
con un incremento di 10.4 Vcc. - 10 Vcc. = 0.4 Vcc.
L'entità di questo modesto incremento, 0.4 Vcc su 10 Vcc è difficilmente misurabile, e non consente la scoperta
del segnale S.
Se esaminiamo i due incrementi come percentuali del livello della tensione di rumore Vuecc = 10 Vcc abbiamo:
per S/N = 0.5; Perc. = ( 2.27 Vurcc x 100 ) / 10 Vurcc = 22 %
per S/N = 0.2; Perc = ( 0.4 Vurcc x 100 ) / 10 Vurcc = 4 %
Queste percentuali, indipendenti dal guadagno G del rivelatore d'energia, saranno utili per il confronto
tra rivelazione d'energia e correlazione.
La curva di figura 8 mostra l'andamento dell'incremento in funzione del rapporto tra segnale e disturbo
con riferimento ad un generico livello del rumore del mare fissato ad 1; la funzione che genera il grafico è:
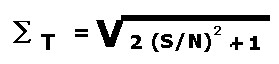
figura 8
Per concludere il paragrafo possiamo dire che il funzionamento del rivelatore d'energia si basa sulla somma delle
tensioni idrofoniche
secondo l'espressione formale:
Vu = ( N1* + S1* ) + ( N2* + S1* )
dove la somma indicata di N* con S* segue i criteri di somma in tensione per S e in potenza per N esposti
in precedenza.
4)Le tecniche di correlazione per la rivelazione dei segnali mascherati dal disturbo 5)La varianza nei correlatori digitali 6)Computazioni, simulazioni e controlli su correlatori digitali
Un sistema di correlazione, a differenza del rivelatore d'energia, se il gruppo idrofonico è costituito
da 2 soli elementi
non impiega alcun sommatore: le tensioni degli idrofoni sono applicate direttamente al sistema così come mostra
figura 9:
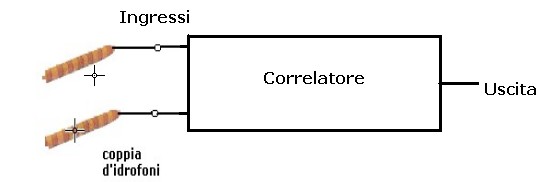figura 9
Dal punto di vista relativo al livello d'uscita del correlatore rispetto al rivelatore d'energia il primo,
quando le tensioni idrofoniche sono incoerenti, presenta
tensione continua a livello 0 più una componente perturbante detta "varianza"; è per questa caratteristica che la
capacità di discriminazione del segnale da parte del correlatore è superiore, come vedremo, a quella del rivelatore di energia.
Il correlatore, invece della somma delle tensioni idrofoniche ne esegue il prodotto secondo l'espressione formale;
Vu = ( N1* + S1* ) X ( N2* + S1* )
L'operazione di moltiplicazione sopra indicata non è agevole da svilupparsi per via analogica data la difficoltà
di messa a punto dei circuiti elettronici necessari; se invece di moltiplicare i segnali in ampiezza e segno si
esegue l'operazione utilizzando soltantanto i segni si ottengono ottimi risultati con circuitazione semplice; il
correlatore che funziona su tale principio è denominato correlatore a coincidenza di polarità o correlatore digitale.
Per trasformare i segnali idrofonici da analogici ( ampiezze e segni ) in segnali a due stati ( solo i segni )
si limitano in ampiezza le tensioni idrofoniche da applicare al correlatore così come mostra la figura 10:
.
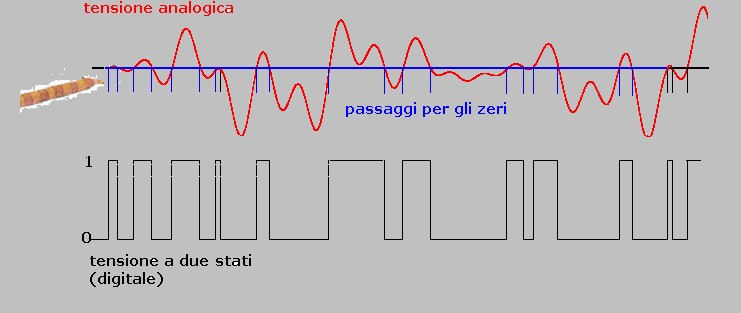figura 10
La figura mostra il segnale analogico in rosso, i suoi passaggi per gli zeri in blu e la conseguente forma del
segnale limitato in ampiezza, in nero, quest'ultima cambia segno ( 0 od 1 ) ogni
qualvolta la tensione analogica, ondulando, passa per il valore 0.
Quando le tensioni idrofoniche sona trasformate in tensioni a due stati l'operazione di moltiplicazione tra esse
è una semplice funzione logica di tipo nor esclusivo, il cui circuito e risposta logica sono mostrate in figura 11:
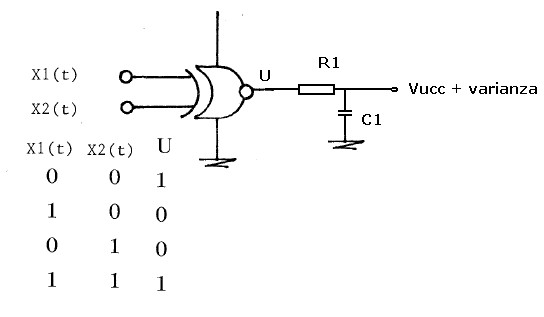figura 11
L'uscita U del circuito esegue la funzione logica riportata nella tabellina mentre il gruppo R1 C1, sommando nel tempo
i successivi stati di U ( processo d'integrazione ), rende una tensione continua Vucc + varianza.
La struttura di figura 11 è di fatto un correlatore in grado di rivelare un segnale coerente mascherato da rumori
incoerenti.
Il livello di tensione continua ai capi di C1, per una tensione di alimentazione del circuito logico di +10 V, segue
il seguente prospetto in dipendenza dello stato dei segnali applicati:
-Per segnali d'ingresso coerenti si ha Vucc = + 10V
-Per segnali d'ingresso incoerenti si ha Vucc = + 5 V
-Il livello Vucc = 0 V si riscontra in casi molto particolari di coerenza tra i segnali
Per rendere più perspicuo l'impiego del correlatore, ed avere livello Vucc = 0 quando i segnali sono incoerenti,
si trasla verso il basso la tensione ai capi di C1, nel nostro caso di 5 Vcc, tramite il circuito di figura 11a
derivato dal circuito di figura 11:
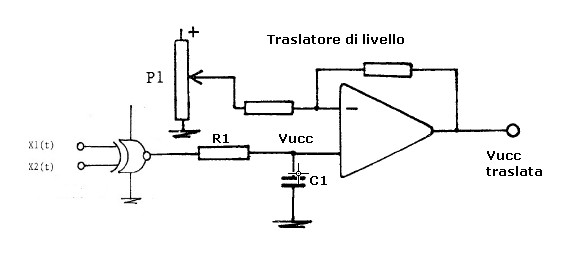figura 11a
Con il circuito di figura 11a il prospetto precedente diventa:
-Per segnali d'ingresso coerenti si ha Vucc = + 5 V
-Per segnali d'ingresso incoerenti si ha Vucc = 0 V
-Il livello Vucc = - 5 V si riscontra in casi molto particolari di coerenza tra i segnali
Una dimostrazione numerica semplice del funzionamento del correlatore in dipendenza del rapporto tra segnale
e disturbo ( S/N ), simile a quella del rivelatore d'energia,
non è possibile, è invece tracciabile una curva del tipo riportato in figura 12 ottenuta applicando la formula:
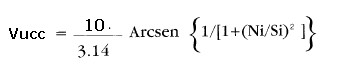espressione 1)
L'espressione, calibrata per il circuito di figura 11a ( CMOS alimentato a 10V ), consente il calcolo
dell'ampiezza della Vucc all'uscita del correlatore del circuito citato in dipendenza del rapporto Segnale/Disturbo ( S/N )
Nella formula il valore massimo raggiungibile nell'ipotesi che il rumore N sia nullo è Vucc = + 5 V,
quando invece il segnale è uguale al rumore : S / N = 1 è Vucc = + 1.65 V.
Per segnale S assente: S = 0; è Vucc = 0 + varianza come mostra figura 12:
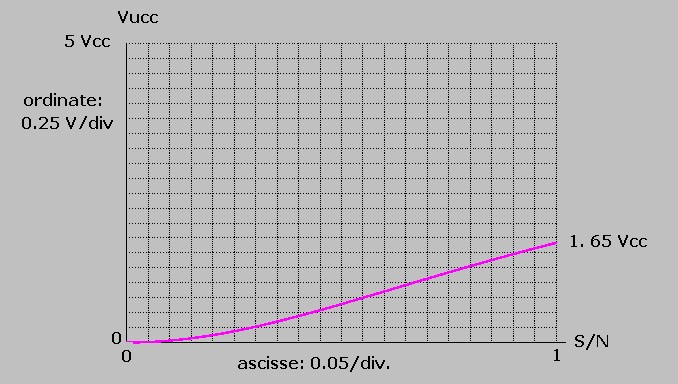figura 12
La curva è tracciata tra S/N = 0 ( assenza di segnale ) e S/N = 1 ( segnale e rumore sono di uguale ampiezza )
In corrispondenza di questi due rapporti di S/N la Vucc del correlatore varia da : Vucc = 0 a Vucc = 1.65.
Si osservi che, per semplicità espositiva, ne la formula ne il grafico mostrano la "varianza" che invece
è d'importanza rilevante per questi sistemi; l'ampiezza
della varianza dipende dal prodotto R1 x C1 di figura 11a; se tale valore cresce la varianza diminuisce ma il correlatore
ha una riduzione della velocità di risposta ; anche per il correlatore come per il rivelatore d'energia
un giusto compromesso và scelto in base delle necessità operative; della varianza tratteremo in dettaglio
al paragrafo seguente.
Il calcolo delle percentuali d'incremento della tensione in uscita del rivelatore d'energia ha avuto come
riferimento la tensione continua dovuta al solo rumore del mare; nel caso del correlatore il riferimento
dovrebbe essere fatto su Vucc = 0 più la varianza.
Per avere un'idea della percentuale d'incremento della Vcc in uscita dal correlatore in dipendenza del rapporto
S/N dei segnali d'ingresso, non potendola calcolare rispetto al livello 0, possiamo supporre che il circuito
di figura 11a (CMOS alimentato a 10Vcc) abbia un fuori zero di + 0.1 Vcc; in tal caso
per S/N = 0 la Vucc d'uscita sarà + 0.1 Vcc; se ora assumiamo il rapporto S/N = 0.2, già utilizzato nell'esempio di
paragrafo 3, la tensione d'uscita del correlatore, in base alla curva di figura 12, è + 0.12 Vucc.
con un livello di tensione totale VTcc all'uscita del correlatore di:
VTcc = Vucc(fuori zero) + Vucc = + 0.1 + 0.12 = + 0.22
con incremento di + 0.12 su + 0.1 pari ad una percentuale del ( 0.12 x 100 ) / 0.1 = 120 %.
Il confronto tra le caratteristiche del rivelatore d'energia e il correlatore, in questo esempio atipico, mostra:
per S/N = 0.2 il primo ha un incremento della tensione d'uscita del 4% il secondo del 120 % !!!
Quanto sopra, naturalmente, ignorando volutamente la "varianza" che, come mostreremo nel paragrafo seguente,
ha un notevole incidenza sulla capacità di discriminazione del correlatore.
L'effetto della varianza sulla capacità di discriminazione di un correlatore digitale è di notevole importanza;
un'idea del comportamento della sua tensione d'uscita è illustrato in figura 13 dove si mostra il confronto
tra l'uscita del correlatore, in assenza di varianza ( caso ideale ) e lo stesso in presenza della varianza ( caso reale ) :
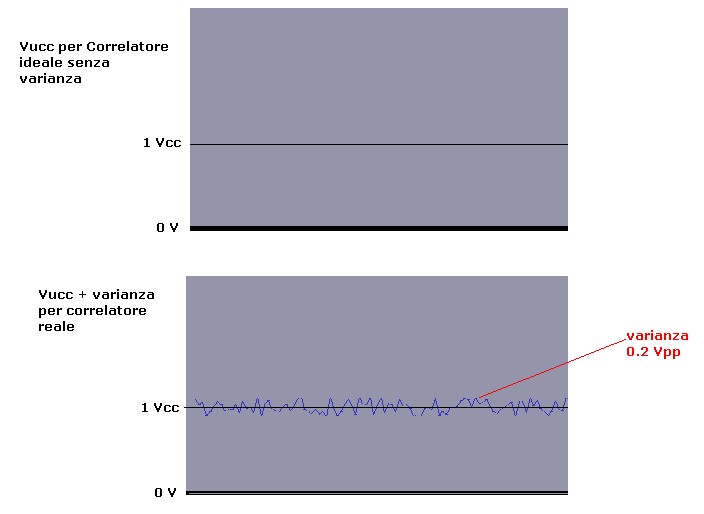figura 13
Il calcolo della varianza ( Nu ), nei correlatori digitali, non dipende dal rapporto tra il segnale e il
disturbo ma
dal valore di R1 x C1 espresso in secondi (costante di tempo d'integrazione ) e dalla banda delle frequenze del rumore indicata con ( F2 -F1 ) così come mostra
la formula seguente:
espressione 2
calibrata per circuito di figura 11 ( CMOS alimentato a 10V )
L'andamento di Nu in funzione del prodotto R1xC1 espresso in secondi è riportato in figura 14 per una banda di frequenza
che si estende tra F1 = 1000 Hz e F2 = 3000 Hz:
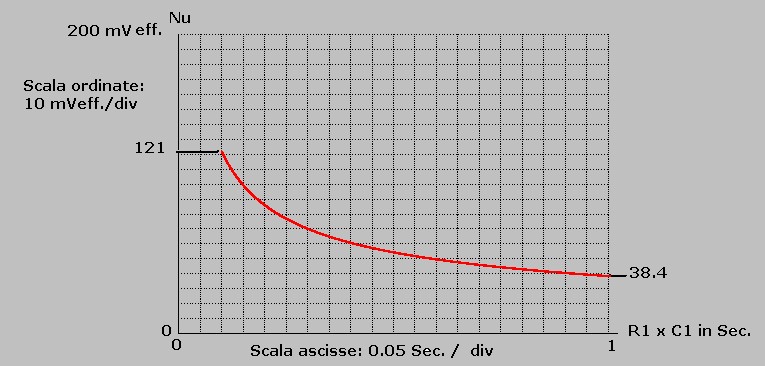figura 14
La curva ha in ascisse il valore di R1 x C1 espresso in secondi, in ordinate il valore efficace di Nu tra Nu = 0
e Nu = 200 mVeff , con un livello di rumore Nu = 121 mV eff. per R1xC1 = 0.1 Sec
e Nu = 38.4 mVeff per R1xC1 = 1 Sec.
Per valutare ora l'effetto della varianza in un correlatore digitale prendiamo ad esempio il circuito di figura
11a che supponiamo ora con fuori zero nullo; se assumiamo S/N = 0.3, in base alla curva di figura 12,
il livello d'uscita del correlatore è di 0.26 Vcc ( 260 mVcc ).
Se supponiamo ora che per necessità operative il prodotto R1xC1 sia: R1xC1 = 0.5 Sec e che la banda del
segnale sia fissata a 2000 Hz da figura 14 si ricava il valore della varianza : Nu = 53 mV eff. con un valore
V(picco - picco) ( per il rumore può essere considerato pari a circa 4 volte il valore eff.) abbiamo;
Nupp. = 53 mVeff. x 4 = 202 mVpp ; come si vede il valore della varianza è inferiore al livello
di uscita del correlatore che in questo caso consentirà di rivelare con certezza la presenza del bersaglio così
come mostra la figura 15.
figura 15
L'uscita del correlatore è di fatto una tensione ondulante la cui ampiezza varia entro la fascia della varianza
intorno al livello di 260 mVcc restando, nei valori minimi, sempre nettamente superiore allo zero.
Concludiamo questa pagina con una serie di figure molto interessanti che mostrano, in un ampio
intervallo del
rapporto S/N, come varia la Vucc al variare di S/N e come la varianza la perturbi.
La figura dell'andamento teorico della Vucc di un correlatore digitale:
La prima figura, il numero 16, mostra l'andamento teorico della Vucc all'uscita di un correlatore digitale al
variare
del rapporto S/N ; il grafico, di colore rosso, segue l'andamento dell'espressione 1) del paragrafo 4), è di fatto
un'estensione della curva di figura 12 computata in un più ampio intervallo della variabilità di S/N.
Questa curva teorica consente il controllo dell'andamento della Vucc di un correlatore dopo la
sua costruzione in laboratorio, i rilievi sperimentali che mirano a stabilire il corretto funzionamento del
correlatore al variare del rapporto segnale/disturbo devono essere, ragionevolmente, coincidenti con la curva
calcolata.
La curva di figura 16 è tracciata con:
-il rapporto S/N in ascisse che varia da 0.06 a 16 con scala non lineare.
-la Vucc, nelle ordinate varia da 0V a + 5 V con scala lineare (0.5V/div)
-assenza di varianza perché l'espressione 1) non la calcola.
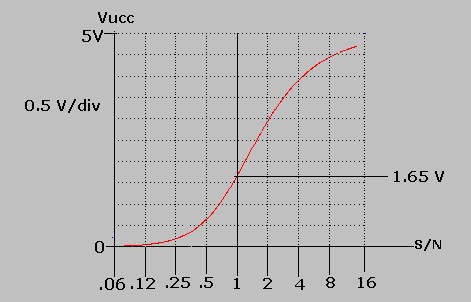figura 16
La figura dell'andamento sperimentale di un correlatore digitale:
A scopo di studio è stata sviluppata una routine software in grado di simulare il funzionamento di un
correlatore in laboratorio; si generano matematicamente:
-la funzione logica ed analogica di figura 11a
-il segnale S
-il rumore N
-la costante di tempo R1xC1
-il rapporto S/N
Il risultato, riportato in figura 17, è lo stesso che potrebbe essere ottenuto in laboratorio da un
correlatore fisico con l'uscita Vucc collegata ad un oscilloscopio:
La curva di figura 17, tracciata in blu, ha:
-il rapporto S/N in ascisse che varia da 0.06 a 16 con scala non lineare.
-la Vucc, nelle ordinate varia da 0V a + 5 V con scala lineare (0.5V/div)
-il profilo seghettato per effetto della varianza che perturba la Vucc
-l'ampiezza della perturbazione è dipendente dal valore simulato di R1xC1, in questo esempio
R1xC1 = 1 Sec.
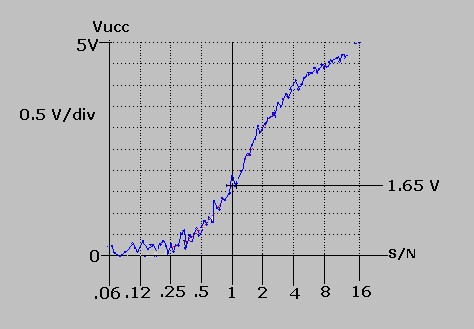figura 17
La figura del confronto tra curva teorica e curva sperimentale di un correlatore digitale:
Per chiudere questo argomento mostriamo in figura 18 la sovrapposizione delle due curve precedenti
per vedere quanto la seconda ( sperimentale ) coincida mediamente con la prima ( teorica ); si noti come
in questa figura la varianza sia riportata per punti indicanti l'escursione massima e non la seghettatura
di figura 17 che maschererebbe il tracciato rosso.
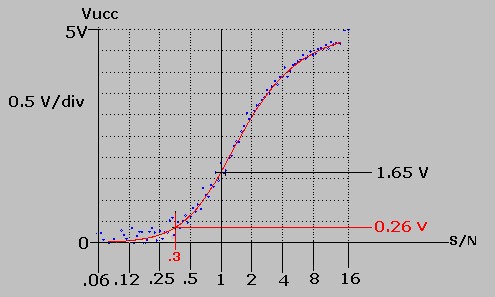figura 18
Nella figura 18 possiamo vedere come la curva teorica passi nella media dell'ampiezza della varianza confermando,
in questo caso, che la simulazione software è aderente alla condizione reale voluta.
In figura sono evidenziate con cifre rosse l'ascissa S/N = 0.3 è l'ordinata VUcc = 0.26 V utilizzate per l'esempio
di paragrafo 5); per questo si può vedere che per S/N = 0.3 la Vucc e Nupp rispondono alle computazioni fatte
in detto paragrafo.