SONAR-INFO-p69
Geometria analitica (8°)
Relazioni tra parabola e rette
1)Generalità 2)Algoritmi in V.B. per calcolo punti di contatto tra parabola e rette 3)Come si presenta la schermata del file eseguibile 4)Esempio d'utilizzo del programma di calcolo 5)Note
Per venire incontro a numerose richieste per l'estensione dei file eseguibili, dei tipi già
utilizzati in p55 e p57, per la soluzione di
altri problemi di geometria analitica, si illustrano alcune routine di calcolo per la soluzione
di casi diversi che possono essere utili a chi deve cimentarsi in questa
interessante parte della matematica.
Una premessa è necessaria prima del prosieguo della pagina: gli algoritmi utilizzati
non sono dimostrati ma soltanto implementati, a favore del calcolo automatico,
in apposite routine in Visual Basic; per le dimostrazioni si rimanda agli innumerevoli testi
di geometria analitica in commercio.
Le coordinate dei punti di tangenza tra parabola e rette passanti per un punto si calcolano
mediante la soluzione di un sistema di secondo grado che vede coinvolte l'equazioni delle
curve.
In questa pagina è riportato un file eseguibile che consente, in modo rapido, il tracciamento di
una data parabola e, da un punto esterno ad essa,
la costruzione delle sue tangenti.
Il programma scrive inoltre l'equazioni delle due rette trovate.
La soluzione del sistema menzionato presenta sensibili difficoltà di manipolazione dei dati con il
rischio di banali, ma deleteri, errori nel suo sviluppo.
Con l'aiuto del programma eseguibile che andiamo ad illustrare è possibile risolvere i problemi
relativi alla parabola con estrema rapidità e sicurezza dei risultati.
La struttura del programma prevede la grafica e la soluzione del problema con riferimento
al sistema delle due equazioni sotto riportate:
Y = a X^2 + b X + c
Y = m X + n
Gli algoritmi implementati, scritti in linguaggio V.B. sono:
-coordinate del punto esterno alla parabola appartenente alle rette tangenti : (Xo; Yo)
-coefficienti a; b; c dell'equazione della parabola
-la soluzione del sistema:
y = a * x ^ 2 + b * x + c
y = m * x + n
porta, con il vincolo di tangenza tra le curve, alle relazioni relative ai computo dei
coefficienti angolari delle rette :
m1 = (-k2 + Sqr(k2 ^ 2 - 4 * k3)) / 2
m2 = (-k2 - Sqr(k2 ^ 2 - 4 * k3)) / 2
nelle quali:
k2 = -2 * b - 4 * a * Xo
k3 = -4 * a * c + 4 * a * Yo + b ^ 2
dai valori di m1 e m2 si calcolano n1 e n2:
n1 = -m1 * Xo + Yo
n2 = -m2 * Xo + Yo
quindi le equazioni delle due tangenti
yt1 = m1 * x + n1
yt2 = m2 * x + n2
segue il calcolo delle coordinate dei punti di tangenza e del vertice parabola:
xt1 = -(b - m1) / (2 * a)
yt1 = m1 * xt1 + (Yo - m1 * Xo)
xt2 = -(b - m2) / (2 * a)
yt2 = m2 * xt2 + (Yo - m2 * Xo)
xv = -b / (2 * a)
yv = a * xv ^ 2 + b * xv + c
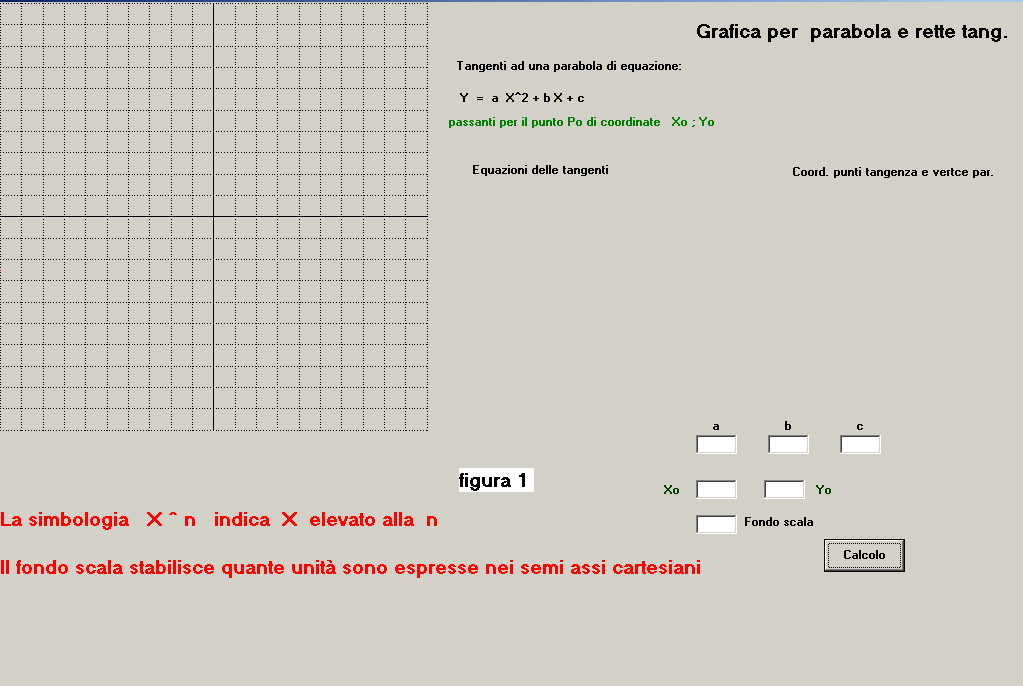
La schermata del file eseguibile, al lancio sul P.C, si presenta come mostrato in figura 1,
in essa s'individuano:
-il tracciato cartesiano
-la sezione per l'inserzione dati comprendente 6 TextBox ed un pulsante di comando.
nella parte alta si digitano i dati: a; b; c; indicati in nero, relativi alla parabola.
nella parte inferiore si digitano i dati Xo; Yo, indicati in verde, relativi alle coordinate
del punto di passaggio delle tangenti quando queste siano possibili.
-la casella per l'inserimento del valore di scala relativo al tracciato cartesiano
In questo paragrafo sono proposti tre esercizi grafico numerici la cui risoluzione è basata
sul file eseguibile (eserc.P1t) .
Il primo esercizio è relativo al calcolo delle equazioni di due rette, passanti per
Po (Xo = 3; Yo = 1),
tangenti alla parabola di equazione Y = 0.5 X^2 - 2 X + 4.
Come vedremo in figura 2 il punto Po è esterno alla parabola; condizione indispensabile per
la tangenza di curve ivi passanti.
Dopo la digitazione dei dati e l'impostazione scala a : fondo scala = 10, si preme il pulsante calcolo
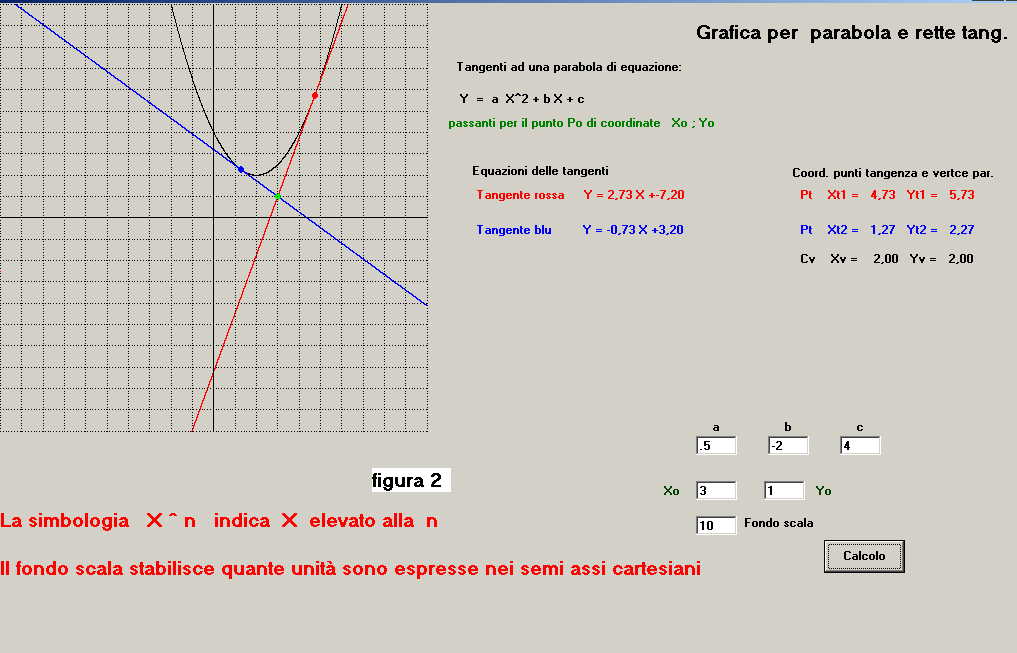
e si ottiene la schermata di figura 2 che indica:
-con un punto color verde il punto Po
-con colore nero la parabola
-con colori rosso e blu le due tangenti
-le equazioni delle due tangenti:
retta rossa: Y = 2.73 X - 7.2
retta blu: Y = -0.73 X + 3.2
-le coordinate dei due punti di tangenza tra le rette e la parabola
con punto rosso: Pt( Xt1 = 4.73 ; Yt1 = 5.73 )
con punto blu: Pt( Xt2 = 1.27 ; Yt2 = 2.27 )
- le coordinate del vertice della parabola Cv ( Xv = 2; Yv = 2 )
Una volta presentati i dati questi possono essere cambiati e , dopo la pressione del pulsante calcolo,
ottenere una presentazione completamente diversa.
.
Secondo esercizio, "Po interno alla parabola", è facilmente ottenibile dal precedente
posizionando Po da :Po (Xo = 3; Yo = 1) a Po (Xo = 2; Yo = 4) lasciando inalterati i coefficienti
a; b; c della parabola.
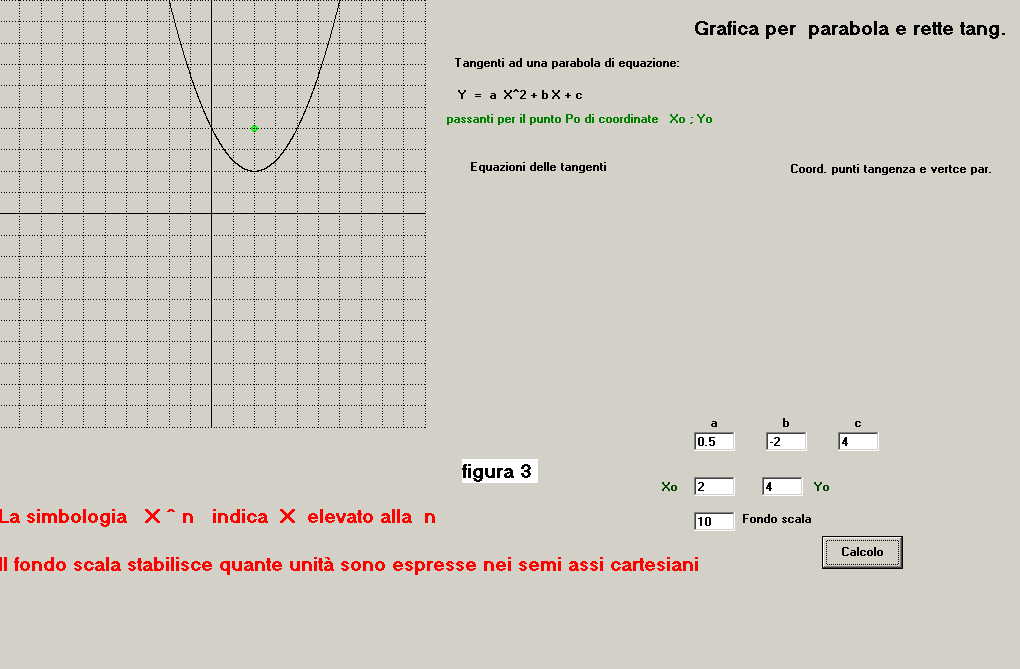
Dopo la digitazione dei dati e l'impostazione scala a : fondo scala = 10, si preme il pulsante
calcolo ottenendo la schermata di figura 3 nella quale si vede la parabola ed il
punto verde Po all'interno di essa; naturalmente nessuna tangente è possibile.
Terzo eserciziorelativo all'utilizzo di valori di scala adattabili alla grafica contingente.
Iniziamo ad impostare questo nuovo esercizio secondo la serie di dati sotto indicati:
a = 1; b = 2; c = 4;
Po ( Xo = 2; Yo = 4)
fondo scala = 10
Dopo l'avvio del calcolo si ha la schermata di figura 4 nella quale non si ha la grafica
del punto di tangenza rosso perché è oltre il tracciato.
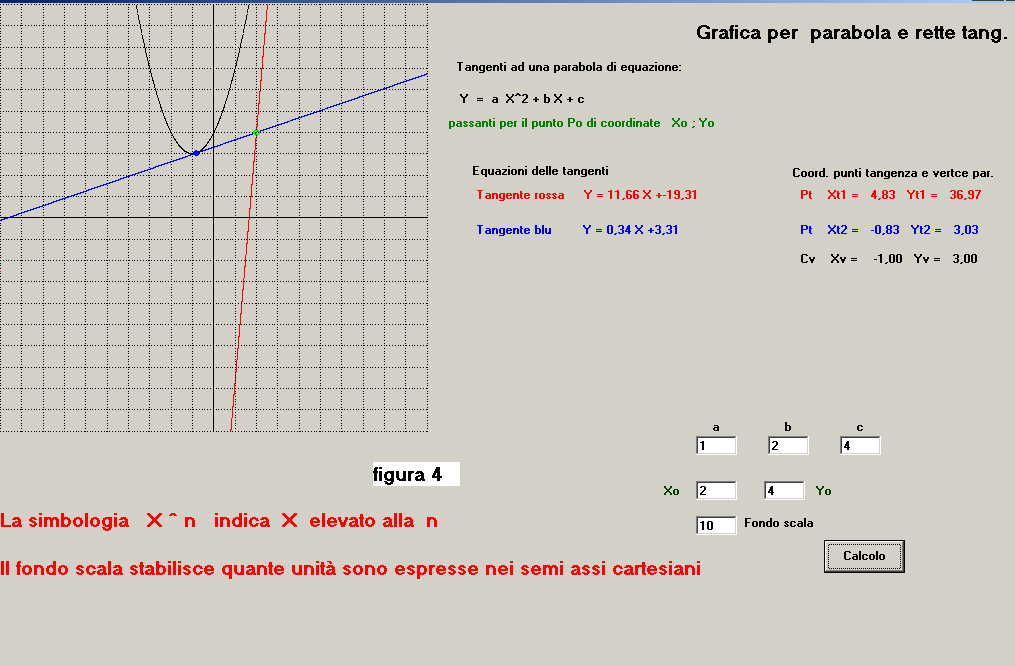
Se osserviamo le coordinate del punto di tangenza rosso le vediamo indicate con:
Pt ( Xt1 = 4.83; Yt1 = 36.97 )
che ci suggerisce una variazione di scala da FS = 10 a Fs = 50 in modo da contenere completamente
il grafico del nostro esercizio; con tale variazione si ottiene infine la schermata completa indicata
in figura5.

-Generalmente i problemi scolastici di geometria analitica mostrano, in tutti i casi, l'impiego
di numeri razionali (frazioni numeriche) o irrazionali (radici quadrate) per l'eleganza formale
del testo; è naturale quindi che per il controllo dei risultati di un problema di tipo scolastico
con l'analogo sviluppato con le nostre routine si dovranno trasformare i valori razionali o
irrazionali esposti per il primo in valori decimali per il confronto con il secondo.
-Il controllo software del file eseguibile è stato eseguito al meglio; è possibile però che
qualche particolare anomalia sia sfuggita all'esame.
Si prega pertanto chi dovesse riscontrare qualche difetto nell'impiego del programma di renderlo
noto tramite " Contatti con l'autore"; si provvederà all'aggiustaggio in rete.