2)Cortina lineare a quattro sensori idrofonici
Lo sviluppo che ci accingiamo a svolgere è necessario per ottenere gli algoritmi di calcolo per il confronto tra le tecniche di rimessa in coerenza e rifasamento dei segnali.
I calcoli interessano una cortina a soli 4 idrofoni al fine di non rendere troppo voluminoso il processo matematico necessario al caso; ciò non toglie che lo stesso percorso concettuale possa essere applicato a cortine con un numero qualsivoglia di sensori.
La cortina lineare è strutturata secondo un segmento sul quale sono allineati i 4 idrofoni da (i1) ad (i4) così come illustrato in figura 1:



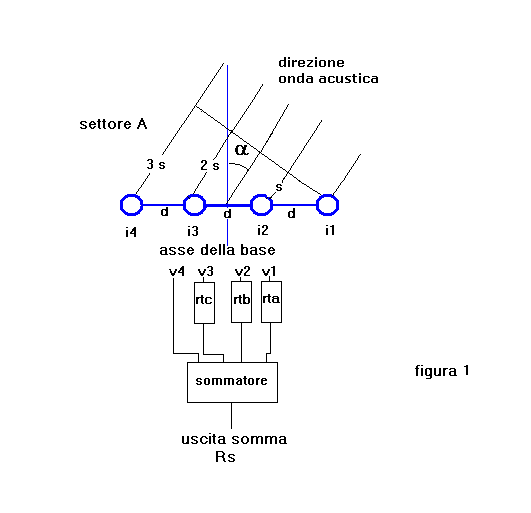
In essa s'individuano gli idrofoni allineati a distanza -d- tra due contigui, l'asse perpendicolare sulla mezzeria dell' allineamento, le cellule di ritardo rta, rtb. rtc e il circuito sommatore che consente la somma dei contributi di tensione forniti dai 4 idrofoni per la composizione di uno dei possibili fasci preformati.
Il fronte d'onda che colpisce la base secondo l'angolo α rispetto all'asse impatta inizialmente il sensore i1, dopo un ulteriore percorso -s- incontra l'idrofono i2, di seguito dopo -2 s- incide sull'idrofono i3 ed infine dopo -3 s- incide sul sensore i4.
Dalla geometria di figura 1 possiamo ricavare facilmente i tempi di percorrenza to, 2 to, 3 to, necessari affinché il suono copra rispettivamente gli spazi s, 2 s, 3 s:
indicata con c la velocità del suono (1530 m/Sec.) il valore di to è
to = d Sen (α) / c
Supponendo il fronte d'onda acustico generato da vibrazioni sinusoidali a frequenza f, le tensioni ai capi dei 4 sensori possono essere espresse in funzione del tempo reale t e dai tempi di ritardo to , 2 to , 3 to :
indicata la velocità angolare con ω = ( 2 π f ) si ha:
-1)
v1 = Sen ( ω t )
v2 = Sen [ ω ( t + to ) ]
v3 = Sen [ ω ( t + 2 to ) ]
v4 = Sen [ ω ( t + 3 to ) ]

Per l'orientamento del fascio di direttività della base le 4 tensioni sono sommate tra loro attraverso opportuni ritardatori rta, rtb, rtc con i quali compensare i tempi to, 2 to, 3 to, affinché tutti i segnali acustici siano rimessi in coerenza temporale prima della loro somma.
I ritardatori in oggetto sono generalmente a tempo costante indipendentemente dalla frequenza applicata; questa caratteristica importante li rende però poco adatti all'inserimento in spazi ridotti date le loro dimensioni meccaniche.
In presenza di bande di frequenza strette i ritardatori possono essere realizzati con cellule di rifasamento RC, poco ingombranti, che costituiscono l'oggetto della presente pagina.
Il valore dei ritardatori espresso in secondi deve essere:
rta = 3 to
rtb = 2 to
rtc = to

sarà quindi:
rtb = 2 rtc
rta = 3 rtc

Inserendo nella -1) i ritardi indicati si avrà il massimo della caratteristica di direttività, fascio preformato, per la direzione α della sorgente acustica.
Sviluppando si ha:
-2)
v1 = Sen [ ω t + ω ( 3 rtc ) ]
v2 = Sen [ ω t + ω ( to + 2 rtc ) ]
v3 = Sen [ ωt + ω ( 2 to + rtc ) ]
v4 = Sen [ ω t + ω ( 3 to ) ]

Date le 4 tensioni della -2) il segnale all'uscita del sommatore sarà esprimibile tramite le proprie componenti ortogonali:

-3)
Rs = Sen [ω t + ω (3 rtc)] + Sen [ω t + ω (to + 2 rtc)] + Sen [ωt + ω (2 to + rtc)] + Sen [ω t + ω (3 to)]
Rc = Cos [ω t + ω (3 rtc)] + Cos [ω t + ω (to + 2 rtc)] + Cos [ωt + ω (2 to + rtc)] + Cos [ω t + ω (3 to)]

Il cui modulo RD normalizzato rappresenta l'andamento della caratteristica di direttività del fascio:

RD = √( Rs² + Rc² )/4

Con le -3) ora sviluppate esamineremo il comportamento di un fascio di direttività impostato secondo due diverse soluzioni di progetto per evidenziarne le sostanziali differenze:
-prima soluzione paragrafo 3)- struttura per formazione fasci con cellule di ritardo a tempo costante.
-seconda soluzione paragrafo 4)-struttura per la formazione fasci con cellule RC di rifasamento.

3)Rappresentazione grafica di RD della cortina con ritardatori a tempo costante
La rappresentazione grafica di RD è svolta con l'implementazione dell'algoritmo indicato in -3) in apposito programma in VB.
Allo scopo si stabiliscono alcuni valori per sviluppare un esempio:

-si fissa un valore di f: f = 1732 Hz

-si calcola il valore di ω = ( 2 π f )= 10883

-considerazioni sul tempo reale t : nel calcolo di RD qualsiasi valore di t è valido

-calcolo di rtc per l'orientamento del fascio per 9° con struttura a ritardo indipendente da fo:
C = 1530 m/Sec.
d = 0.33 m
α = 9°
da cui rtc = d Sen(α) / c = 33.74 microSec.

-considerazioni sul valore di to:
per l'esplorazione dell'orizzonte nel settore A alla base, essendo to = d Sen(α) / c , faremo variare to variando α da 0° a 90°, alla ricerca del massimo della curva di direttività che troveremo coincidente con il valore α = 9° per il quale abbiamo impostato i valori rtc dei ritardi per la formazione del fascio.
L'andamento di Rd in funzione di α è riportato in figura 2.



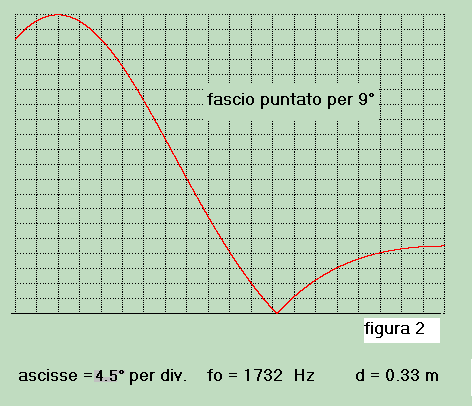
Essendo la curva di direttività di figura 2 relativa ad un sistema a fasci preformati realizzato con ritardatori a tempo indipendente dalla frequenza esso può discriminare segnali acustici in un ampio spettro mantenendo inalterata la direzione del fascio per 9° così come il progetto prevede.

4)Rappresentazione grafica di RD della cortina con ritardatori a cellule RC
Per questo tipo di applicazione si devono esprimere in modo distinto i ritardi rtc, rtb, rta, e non come multipli di rtc come nei paragrafi precedenti.
I valori di rtc, rtb, rta vengono realizzati in funzione dello sfasamento di tre diverse cellule RC calcolato ad una frequenza fo; si verificano quindi le alterazioni di puntamento del fascio in conseguenza delle variazioni di fo.
Allo scopo si stabiliscono alcuni valori per sviluppare un esempio:

-si fissa un valore di fo: fo = 1732 Hz

-si calcola il valore di ω = ( 2 π fo )= 10883

-considerazioni sul tempo reale t : nel calcolo di RD qualsiasi valore di t è valido

-calcolo di rtc per l'orientamento del fascio per 9° con struttura a ritardo variabile:
per ottenere da una cellula RC uno sfasamento Φ tale che la frazione del periodo di fo che ad esso compete sia di:
Sen(α) / c = 33.74 microSec.
lo sfasamento corrispondente è:
Φ = 360 fo (33.74 / 1000000) = 21.037°
fissato per R un valore di 10000 ohm si ha
Xc = R / tang Φ = 10000 / tang(21.037) = 26000 ohm
da cui C :
C = 1 /(6.28 fo Xc) = 3536 pF
ne segue che l'espressione per il calcolo di rtc, in secondi, in funzione della frequenza è:
rtc = [ArcTang ( 6.28 R C fo)] / (360 fo)
che, ovviamente per fo = 1732 è: rtc 33.74 microSec.
L'ampiezza del segnale all'uscita dalla cellula RC, assunto il valore massimo A = 1, è:
A = 1 / √[ 1 + (6.28 fo R C)²] = 0.93

-calcolo di rtb per l'orientamento del fascio per 9° con struttura a ritardo variabile:
per ottenere da una cellula RC uno sfasamento Φ tale che la frazione del periodo di fo che ad esso compete sia di:
2 Sen(α) / c = 67.48 microSec.
lo sfasamento corrispondente è:
Φ = 360 fo (67.48 / 1000000) = 42.074°
fissato per R un valore di 10000 ohm si ha
Xc = R / tang Φ = 10000 / tang(42.074) = 11077 ohm
da cui C :
C = 1 /(6.28 fo Xc) = 8300 pF
ne segue che l'espressione per il calcolo di rtc, in secondi, in funzione della frequenza è:
rtc = [ArcTang ( 6.28 R C fo)] / (360 fo)
che, ovviamente per fo = 1732 è: rtb = 67.48 microSec.
L'ampiezza del segnale all'uscita dalla cellula RC, assunto il valore massimo A = 1, è:
A = 1 / √[ 1 + (6.28 fo R C)²] = 0.74

-calcolo di rta per l'orientamento del fascio per 9° con struttura a ritardo variabile:
per ottenere da una cellula RC uno sfasamento Φ tale che la frazione del periodo di fo che ad esso compete sia di:
3 Sen(α) / c = 101.22 microSec.
lo sfasamento corrispondente è:
Φ = 360 fo (101.22 / 1000000) = 63.11°
fissato per R un valore di 10000 ohm si ha
Xc = R / tang Φ = 10000 / tang(63.11) = 5071 ohm
da cui C :
C = 1 /(6.28 fo Xc) = 18130 pF
ne segue che l'espressione per il calcolo di rtc, in secondi, in funzione della frequenza è:
rta = [ArcTang ( 6.28 R C fo)] / (360 fo)
che, ovviamente per fo = 1732 è: rta = 101.22 microSec
L'ampiezza del segnale all'uscita dalla cellula RC, assunto il valore massimo A = 1, è:
A = 1 / √[ 1 + (6.28 fo R C)²] = 0.45

-considerazioni sul valore di to:
per l'esplorazione dell'orizzonte sul settore A alla base, essendo to = d Sen(α) / c , faremo variare to variando α da 0° a 90°, alla ricerca del massimo della curva di direttività che troveremo coincidente con il valore α = 9° per fo = 1732 Hz per il quale abbiamo impostato i valori rtc, rtb, rta, dei ritardi per la formazione del fascio.

L'andamento di Rd in funzione di α, con le ampiezze dei segnali sfasati riportate allo stesso livello e per
fo = 1732 Hz e 3464 Hz è riportato in figura 3 .



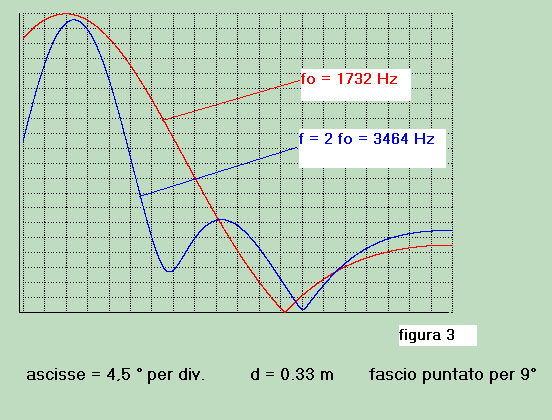
La curva rossa, tracciata per fo = 1732, è correttamente puntata su 9° così come deve in base al calcolo di rta, rtb, rtc sviluppato per tale frequenza.
La curva blu, tracciata per f = 2 fo = 3464 Hz, mostra che la direzione del fascio è puntata per circa 10.8° con un errore di + 1.8°.
Una tabella dell'errore di puntamento è tracciata per una serie di valori di f rilevati su diverse curve simili a quelle di figura 3:

Dalla tabella si è composto il grafico di figura 4 per meglio evidenziare l'andamento dell'errore di puntamento del fascio in funzione della frequenza.



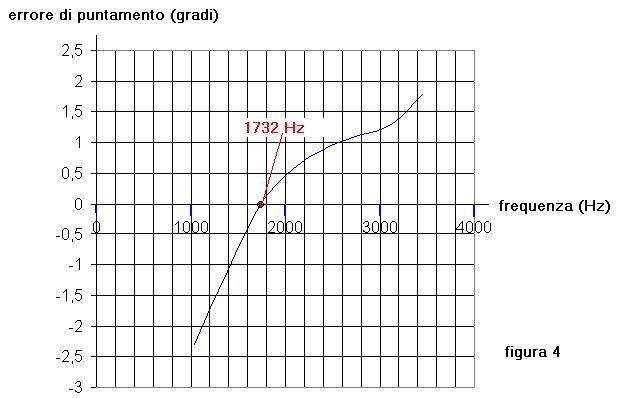
La generazione dell'errore, già annunciata, mostra come il metodo di formazione fasci con cellule RC sia adatto per piccole bande di frequenza, quali ad esempio gli echi dei bersagli nella fase della ricerca sonar con metodi attivi.
In questi casi la frequenza di emissione è, generalmente, costante e la frequenza dell'eco può essere alterata soltanto a causa dell'effetto Doppler.
Nel caso numerico in esame supponendo una durata d'impulso di 60 mSec. e ipotizzando una velocità relativa tra emettitore e bersaglio di 40 nodi, avremo la seguente banda di frequenza:
-per la durata dell'impulso Δfi = 1 / 0.06 = 17 Hz
-per l'effetto Doppler Δfd = 49 Hz    (si veda p35)
Con una variazione di fo da ≈ 1724 Hz a ≈ 1790 Hz.
Dal grafico di figura 4 si evince che, in questo caso, l'errore di puntamento del fascio è irrilevante.

5)Osservazioni
Come abbiamo visto il metodo di rifasamento con cellule RC è adatto per la formazione dei fasci in bande di frequenze relativamente strette e si adatta molto bene alla scoperta nei sonar attivi.
Si deve tener presente che per la realizzazione delle cellule RC, onde evitare che l'ampiezza A del segnale rifasato vari con il valore di C, si può utilizzare la configurazione della cellula riportata in figura 5; tale circuito, a parità di valori di R e C, genera però uno sfasamento doppio del quale si deve tenere conto:



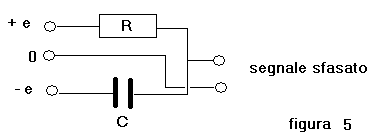
Il calcolo della cellula RC per il circuito di figura 5 si esegue partendo dagli sfasamenti voluti nello sviluppo del paragrafo 4) e dividendo per 2 tali valori:
21.037° / 2 = 10.52° per il primo
42.74° / 2 = 21.037° per il secondo
63.11° / 2 = 31.55° per il terzo
per procedere ad un nuovo calcolo delle capacità:

Per rtc - fissato per R un valore di 10000 ohm si ha
Xc = R / tang Φ = 10000 / tang(10.52) = 53850 ohm
da cui C :
C = 1 /(6.28 fo Xc) = 1707 pF

Per rtb - fissato per R un valore di 10000 ohm si ha
Xc = R / tang Φ = 10000 / tang(21.037) = 26000 ohm
da cui C :
C = 1 /(6.28 fo Xc) = 3536 pF

Per rta - fissato per R un valore di 10000 ohm si ha
Xc = R / tang Φ = 10000 / tang(31.55) = 16267 ohm
da cui C :
C = 1 /(6.28 fo Xc) = 5652 pF

Un ultimo rilievo deve essere fatto in merito alla perdita di parte del segnale impulsivo; questo fenomeno si verifica dato che il segnale viene rifasato e sommato con i contributi di tutti i sensori della base solt
anto dopo che ha percorso lo spazio 3s.
Si perde pertanto, nel nostro caso, una porzione di durata pari a ≈ 6 d / c = 6 ⋅ 0.33 /1530 = 4 mSec.

6)Appendice
Visto l'impiego, nel paragrafo 5), di un circuito di sfasamento semplice ma poco noto si ritiene interessante un confronto teorico tra la cellula RC classica e questa diversa soluzione.
Allo scopo si fa riferimento alle figure 6a e 6b dalle quali dedurre le impostazioni matematiche per la loro definizione:




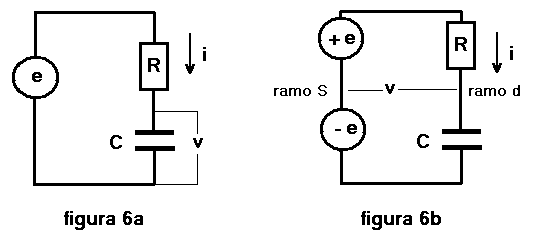
Soluzione per la cellula RC classica , figura 6a:
la corrente (i) che scorre nella rete è:
i = e / ( R + j Xc )
la tensione (v) ai capi di (C) risulta:
V = i ⋅ jXc = [ e / ( R + j Xc ) ] ⋅ jXc
che normalizzata per e = 1 diventa:
V = jXc / ( R + j Xc )
sviluppando per eliminare il numero complesso a denominatore si ha:
V = [ Xc² / ( R² + Xc² ) ] + j [ R Xc / ( R² + Xc² ) ]
dal quale si ricavano argomento ( θ ) e modulo (M):
θ = ArcTang ( R / Xc )
M = Xc / √( R² + Xc² )

Osservazioni sui valori ( θ ) e (M)
per Xc = R    si ricavano i noti valori di:   θ = 45°   e  M = 0.707

Soluzione per la cellula di figura 6b:
indicata con (V) la tensione tra i due rami (s) e (d) e con (i) la corrente che scorre nei rami si può esprimere (V) con due equazioni diverse in un sistema:
V = +e + R ⋅ i
V = -e + jXc ⋅ i
che risolto in (i) e normalizzando per e = 1 da:
i = 2 ( jXc - R )
con il valore di (i) ricavato si risolve il sistema per (V) ottenendo, dopo diversi passaggi, il numero complesso che esprime (V):
V = [ ( R² - Xc² ) / ( R² + Xc² ) ] + [ j 2 R Xc / ( R² + Xc² ) ]
dal quale si ricavano argomento ( θ ) e modulo (M):
θ = ArcTang [ ( 2 R Xc / ( R² - Xc² ) ]
M = ( R² + Xc² ) / ( R² + Xc² )

Osservazioni sui valori ( θ ) e (M)
per Xc = R    si ricava:   θ = 90°   e  M = 1

Come si vede il modulo M è indipendente da R e Xc mentre l'argomento θ assume un valore doppio rispetto alla cellula RC classica.










Home

Stampa immagine grafica o descrizione testuale