Geometria analitica (13°)
Relazioni tra parabole e circonferenze

1)Generalità
Per venire incontro a numerose richieste per l'estensione dei file eseguibili, dei tipi già utilizzati in p55 e p57, per la soluzione di altri problemi di geometria analitica, si illustrano alcune routine di calcolo per la soluzione di casi diversi che possono essere utili a chi deve cimentarsi in questa interessante parte della matematica.
Una premessa è necessaria prima del prosieguo della pagina: gli algoritmi utilizzati non sono dimostrati ma soltanto implementati, a favore del calcolo automatico, in apposite routine in Visual Basic; per le dimostrazioni si rimanda agli innumerevoli testi di geometria analitica in commercio.

2)Algoritmi in V.B. per il calcolo dell'equazioni e dei punti di contatto tra parabola asse verticale e circonferenza.
Le coordinate dei punti di contatto tra parabola con asse verticale e cerchio, siano tangenti che secanti, si devono trovare mediante la soluzione di un sistema di quarto grado che vede coinvolte l'equazioni delle due curve.
Il sistema menzionato non si presta a soluzioni puramente algebriche e richiede metodi diversi per la determinazione delle sue radici quando queste vi siano.
Con l'aiuto del programma eseguibile che andiamo ad illustrare è possibile risolvere il problema con estrema rapidità e sicurezza dei risultati.
La struttura del programma prevede la grafica e la soluzione del problema con riferimento al sistema delle due equazioni sotto riportate:

Y = ao X^2 + bo X + co
X^2 + Y^2 + a X + b Y + c = 0

La prima equazione è relativa ad una parabola ad asse verticale, la seconda ad una circonferenza.
Il calcolo prevede l'introduzione dei valori dei coefficienti (ao; bo; co) per la parabola e le coordinate di tre punti di passaggio per la circonferenza: p1(X1; Y1) p2(X2; Y2) p3(X3; Y3).
Nel caso che il problema sia posto nei termini delle variabili citate l'impiego del programma è immediato, nei casi invece che:
-per la parabola siano disponibili le tre coordinate dei punti di passaggio, i coefficienti ao; bo; co; richiesti dal programma potranno essere determinati tramite l'eseguibile esposto in p71.
-per il cerchio sia data l'equazione completa sarà facile, mediante l'impostazione di tre valori di X (X1; X2; X3) trovare i corrispondenti valori di Y ( Y1; Y2; Y3).
Gli algoritmi implementati, scritti in linguaggio V.B. sono:

per la parabola asse verticale:
j = av * X^2 + bv * X + cv
dove av = ao; bv = bo; cv = co

per la composizione dell'equazione dei due rami della circonferenza:
k1 = -(X1 ^ 2 + Y1 ^ 2)
k2 = -(X2 ^ 2 + Y2 ^ 2)
k3 = -(X3 ^ 2 + Y3 ^ 2)
d1 = X1 * Y2 + Y1 * X3 + X2 * Y3
d2 = Y2 * X3 + X1 * Y3 + Y1 * X2
delta = d1 - d2
da1 = k1 * Y2 + k3 * Y1 + k2 * Y3
da2 = k3 * Y2 + k1 * Y3 + k2 * Y1
deltaa = da1 - da2
db1 = X1 * k2 + k1 * X3 + k3 * X2
db2 = k2 * X3 + k3 * X1 + k1 * X2
deltab = db1 - db2
dc1 = X1 * Y2 * k3 + Y1 * k2 * X3 + k1 * X2 * Y3
dc2 = k1 * Y2 * X3 + X1 * k2 * Y3 + Y1 * X2 * k3
deltac = dc1 - dc2
a = deltaa / delta
b = deltab / delta
c = deltac / delta

il calcolo del raggio e le coordinate del centro
r = Sqr((a / 2) ^ 2 + (b / 2) ^ 2 - c)
alfa = -a / 2
beta = -b / 2

la costruzione delle due curve:
j = av * X1v ^ 2 + bv * X1v + cv
Y1 = (Sqr(0.00321 + r ^ 2 - (X1v - alfa) ^ 2)) + beta
Y2 = -(Sqr(0.00321 + r ^ 2 - (X1v - alfa) ^ 2)) + beta

le somme condizionate:
z1 = -(Y1 - j)
z2 = -(Y2 - j)

per la ricerca condizionata, con anelli for.., degli zeri di z1 e z2 (ascisse dei punti di contatto)
z1 = (Y1 - j)
z2 = (Y2 - j)

il controllo della validità degli zeri trovati e calcolo, tramite le funzioni Y1; Y2; J, delle corrispondenti ordinate.

il tracciamento delle curve e indicazione numerica delle coordinate dei punti di contatto.

3)Come si presenta la schermata del file eseguibile
La schermata del file eseguibile, al lancio sul P.C, si presenta come mostrato in figura 1, in essa s'individuano:

-il tracciato cartesiano
-la sezione per l'inserzione delle coordinate (x1;y1) (x2;y2) (x3; y3), dei punti appartenenti alla circonferenza
-la sezione per l'inserzione dei coefficienti, ao; bo; co; della parabola con asse verticale.
-il pulsante per la grafica e il calcolo delle coordinate dei punti di contatto
-la casella per l'inserimento del valore di scala relativo al tracciato cartesiano
-otto Label per la presentazione delle coordinate dei punti di contatto
-sotto le formula del cerchio, a calcolo ultimato, compaiono i valori del raggio e le coordinate del centro.
-sotto le formula della parabola, a calcolo ultimato, compaiono i valori ao; bo; co.
I tracciati delle due curve sono a tratto nero così come i punti che definiscono la posizione della circonferenza. I punti di contatto tra le due curve sono identificati da cerchietti colorati, rosso; verde; blu; magenta, che aiutano all'individuazione della posizione dei valori delle coordinate calcolate che compaiono con colori corrispondenti.
La traccia della parabola con asse verticale può sconfinare il tracciato cartesiano per aiutare, in certe condizioni a stabilire il valore di scala più adatto all'esercizio.
In alcuni casi, quando i punti di contatto tra le curve sono fuori dal reticolo, a causa di un dimensionamento non corretto del "fondo scala" , le indicazioni delle coordinate dei punti di contatto non sono riportate sullo schermo; dall'andamento delle due curve questa condizione può essere individuata e di conseguenza modificata riportando in scala il tracciato.

4)Esempio d'utilizzo del programma di calcolo
In questo paragrafo sono proposti alcuni esercizi grafici numerici la cui risoluzione è basata sul file eseguibile (eserc.Pcer) .
Premessa al calcolo: Il computo delle coordinate dei punti di contatto è possibile soltanto se il valore di fondo scala è commisurato alle dimensioni della circonferenza: il cerchio deve sempre comparire per intero nel tracciato cartesiano.

-primo esercizio " curve secanti su quattro punti :
si considera una parabola convessa con asse verticale: a = - 2; b = 5 ; c = 5
s'individua una circonferenza passante per: p1(x1 = -2; y1 = -2) p2(x2 = 2; y2 = 2) p3(x3 = 5; y3 = 1)
Una volta digitati i dati indicati e il valore di fondo scala = 10, cliccando sul pulsante "Calcolo" sul reticolo cartesiano compaiono le due curve.
A fianco l'indicazione delle quattro coordinate dei punti di contatto contornati dai cerchietti:
p1( X1 = 3.009 ; Y1 = 1.94) - verde -
p2 ( X2 = 3.923 ; Y2 = -6.165) - magenta -
p3( X3 = -.656 ; Y3 = .863) - rosso -
p4 ( X4 = -1.276 ; Y4 = -4.637) - blu -

La grafica è visibile in figura 2:



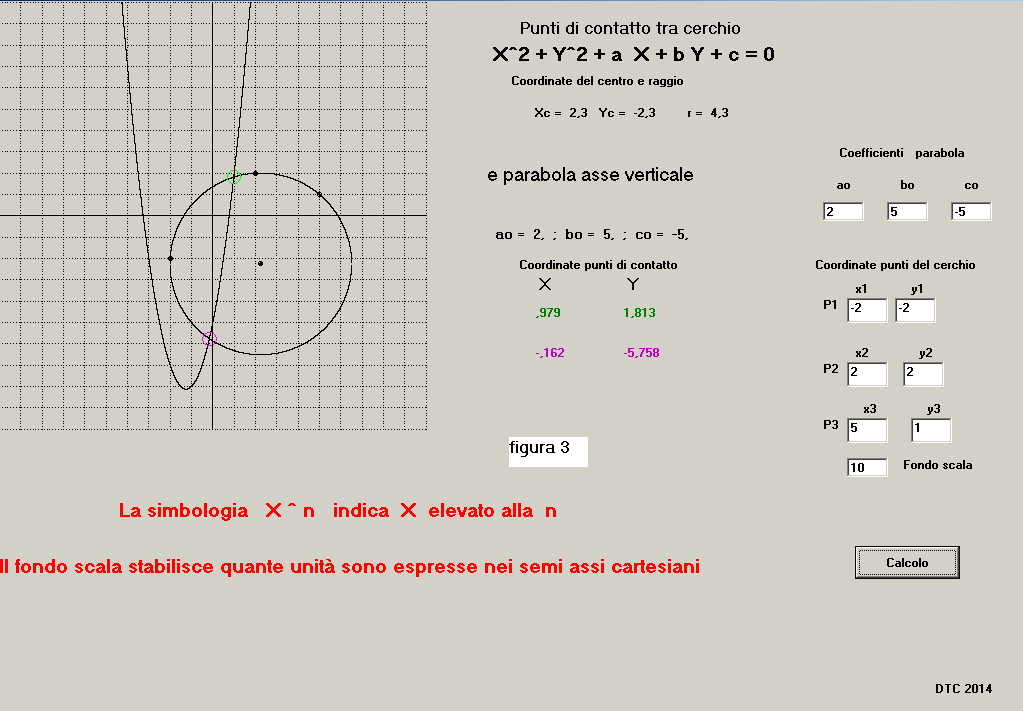
-secondo esercizio " curve secanti per due punti:
ferma restando la circonferenza passante per: p1(x1 = -2; y1 = -2) p2(x2 = 2; y2 = 2) p3(x3 = 5; y3 = 1)
si sviluppa l'esercizio con una diversa parabola con asse verticale; il risultato è riportato in figura 3:



-terzo esercizio " curve non a contatto:
ferma restando la circonferenza passante per: p1(x1 = -2; y1 = -2) p2(x2 = 2; y2 = 2) p3(x3 = 5; y3 = 1)
si sviluppa l'esercizio con una parabola con asse verticale che non interseca la circonferenza; il risultato è riportato in figura 4:



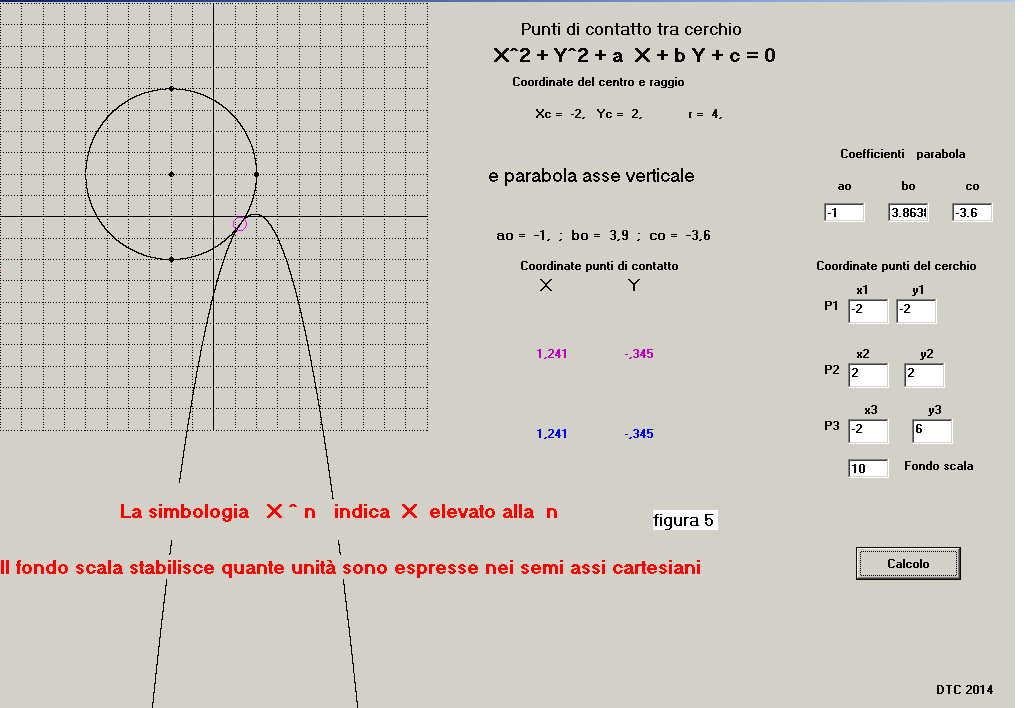
-quarto esercizio " circonferenza passante per i punti: p1(x1 = -2; y1 = -2) p2(x2 = 2; y2 = 2) p3(x3 = -2; y3 = 6)
tangente ad una parabola con asse verticale e coefficienti:
ao = -1; bo = 3.863867; co = -3.6
si ha tangenza per (x = 1.241; y = -.345 )
il risultato è riportato in figura 5:

5)Note
-Generalmente i problemi scolastici di geometria analitica mostrano, in tutti i casi, l'impiego di numeri razionali (frazioni numeriche) o irrazionali (radici quadrate) per l'eleganza formale del testo; è naturale quindi che per il controllo dei risultati di un problema di tipo scolastico con l'analogo sviluppato con le nostre routine si dovranno trasformare i valori razionali o irrazionali esposti per il primo in valori decimali per il confronto con il secondo.

-Il controllo software del file eseguibile è stato eseguito al meglio; è possibile però che qualche particolare anomalia sia sfuggita all'esame.
Si prega pertanto chi dovesse riscontrare qualche difetto nell'impiego del programma di renderlo noto tramite " Contatti con l'autore"; si provvederà all'aggiustaggio in rete.