1) Introduzione
Le curve ROC (receiver operating characteristic curve), studiate da W.W.Peterson, (USA), sono state utilizzate in alcune pagine di questo sito, sotto forma di diagrammi, per lo sviluppo di alcuni elaborati sul sonar e la correlazione .
In questa pagina viene proposto un metodo di calcolo software, per la determinazione di tutte le variabili che interessano i diagrammi citati, al fine di ottenere dati più precisi in una gamma di valori notevolmente più estesa di quella disponibile nelle curve ROC originali.

2)Le curve ROC originali
Le curve ROC originali, riportate in figura 1, mostrano il legame tra la p(FA -probabilità di falso allarme- e la p(D) -probabilità di rivelazione- tramite la variabile (d) dipendente dal rapporto segnale/disturbo all'ingresso del ricevitore sonar; una semplice trattazione su tali variabili è riportata nel testo di pagina p5 - cap.4 che si consiglia di leggere prima dell'esame del presente lavoro.




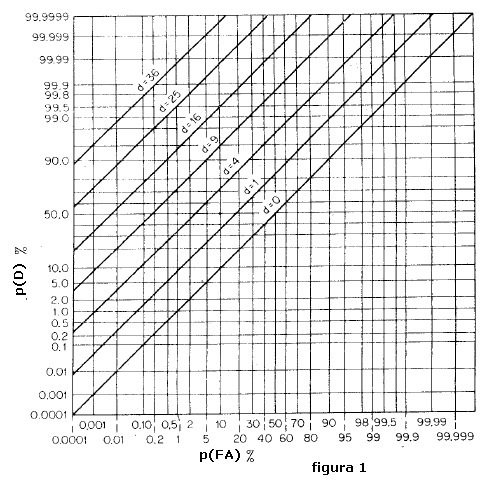
Il dato rilevato dalle curve, un valore del (d) per ciascuna coppia p(FA), p(D), viene utilizzato nelle computazioni relative alle prestazioni dei sistemi riceventi del sonar.
Come si vede da figura 1 i valori della variabile (d) sono soltanto 7 e, date le scale e le dimensioni dei tracciati, resta difficile interpolare con precisione valori del (d) tra quelli esistenti; il seguente esempio sul grafico mostra quanto asserito:
si debba stabilire il valore di (d) nel caso in cui p(FA) = 0.1 % e p(D) = 90 % , l'incrocio delle due coordinate individua un punto compreso tra d = 9 e d = 25, tra questi due valori si deve interpolare, su scala non lineare, il valore corretto della variabile d.
Per consentire un impiego più versatile delle curve ROC è stato sviluppato il software di cui tratteremo nel prosieguo; gli algoritmi che sono utilizzati provengono dai lavori di Peterson e Urick adattati al particolare sviluppo di calcolo ideato per questa pagina.

3)Impostazione teorica degli algoritmi
Gli algoritmi da implementare in software sono divisi in tre sezioni:
Sezione 1 - relativa al calcolo delle variabili che interessano p(FA), la probabilità di falso allarme
Sezione 2 - relativa al calcolo delle variabili che interessano p(D), la probabilità di rivelazione
Sezione 3 - relativa al calcolo del rapporto segnale/disturbo

La sezione 1 è mostrata di seguito:



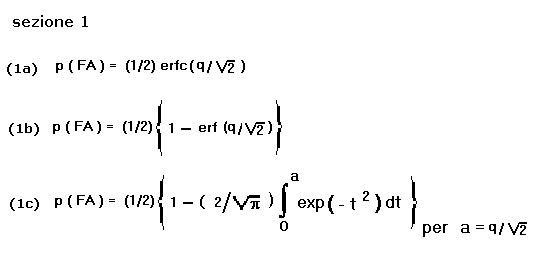
In essa sono riportate tre espressioni, (1a), (1b), (1c):   (1b) e (1c) rappresentano in successione lo sviluppo della prima che andiamo a commentare:
La (1a) mostra la funzione p(FA) dipendente, secondo la "erfc" (funzione d'errore complementare), dalla variabile (q) che rappresenta, in forma normalizzata, il livello del disturbo all'ingresso del ricevitore.
La (1b) mostra la funzione p(FA) trasformata da "erfc" (funzione d'errore complementare), in "erf" (funzione d'errore) sempre in dipendenza di (q).
Per ultima la (1c) che mostra, secondo l'integrale della funzione di Gauss, l'espressione applicativa per il computo del valore numerico di p(FA)= f(q).

La sezione 2 è mostrata di seguito:



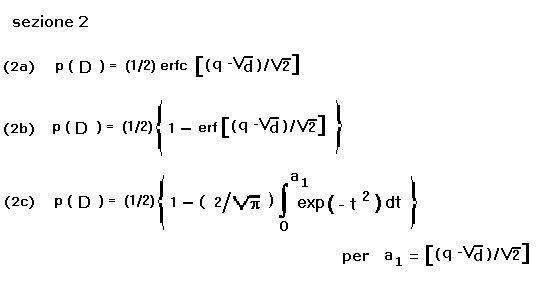
In essa sono riportate tre espressioni, (2a), (2b), (2c):   (2b) e (2c) rappresentano in successione lo sviluppo della prima che andiamo a commentare:
La (2a) mostra la funzione p(D) dipendente, secondo la "erfc" (funzione d'errore complementare), dalle variabili (q) e (d) che rappresentano, in forma normalizzata, rispettivamente il livello del disturbo e il rapporto segnale/disturbo all'ingresso del ricevitore.
La (2b) mostra la funzione p(D) trasformata da "erfc" (funzione d'errore complementare), in "erf" (funzione d'errore) sempre in dipendenza di (q) e (d).
Per ultima la (2c) che mostra, secondo l'integrale della funzione di Gauss, l'espressione applicativa per il computo del valore numerico di p(D)= f(q;d).

Le funzioni (1c) e (2c) sono utilizzabili direttamente, mediante software adatto, per il calcolo di p(FA), come variabile dipendente da (q) e per il calcolo di p(D) come variabile dipendente da (q) e (d); è invece difficoltosa l'operazione inversa per calcolare (q) come funzione di p(FA) e (d) come funzione di p(D) .
A questo scopo è stato studiato il software descritto di seguito che, con processi da calcolo iterativi, raggiunge l'obiettivo prefissato che consente il calcolo del (d), ovvero del rapporto s/n una volta stabilito il valore massimo della p(FA) accettata e della p(D) desiderata.

La sezione 3, mostrata di seguito, è semplice e non richiede commenti:



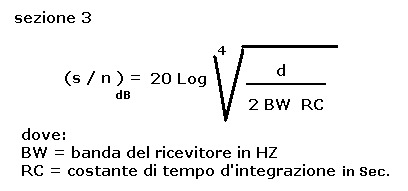
La funzione (1c) di sezione 1; la 2(c) di sezione 2 e la funzione di sezione 3 sono definite tramite processi diretti di calcolo mediante le espressioni analitiche indicate.
Per ciascuna di esse possono essere dichiarate le funzioni inverse:
-per la p(FA) = f(q)     la   q = f[p(FA)]
-per la p(D) = f(q;d)     la   d = f[p(D); q]  e  q = f[p(D); d]
-per la s/n = f(d; BW; RC)   la   d = f ( s/n; BW; RC)
Il calcolo su P.C. delle funzioni dirette è immediato mentre per le funzioni inverse, di tipo analitico, è più laborioso per la necessità d'uso di pesanti routine iterative.

4)Il software per i computi delle funzioni inverse e dirette
Se osserviamo le due funzioni p(FA) e p(D) notiamo che entrambe dipendono dalla variabile (q), ne segue che p(D) dipende da p(FA) tramite la funzione inversa q = f[ p(FA)]; calcolato che sia (q), in funzione di
p(FA), s'imposta il calcolo della seconda funzione inversa che consente la computazione di (d) in funzione di p(D) e (q) tramite p(FA).
Il programma di calcolo, sviluppato in Visual Basic, si presenta con la schermata operativa di figura 2 per un commento:



Sezione 1
- calcolo della funzione inversa: q = f [p(FA)] -
In questa sezione deve iniziare la procedura di calcolo secondo la sequenza:
1) inserzione del valore del p(FA) - nella figura p(FA) = 20 % -
2) si preme il pulsante verde "calcolo var. (q)" che all'inizio del calcolo cambia colore in rosso; questo per evidenziare il tempo di elaborazione che per piccoli valori di p(FA) è di alcuni secondi (dipende dalla velocità del P.C.).
3) alla fine del calcolo il pulsante diventa verde ed il dato è riportato nel rettangolo sottostante; in figura è indicato il valore del (q) calcolato: q = 0.9.
Automaticamente detto valore è reso disponibile per i successivi calcoli nella sezione 2: d = f [ p(D), q)] e p(D) = f[ d; q)].
Nel rettangolo è indicato inoltre il valore di p(FA) che, con il processo iterativo, ha consentito il calcolo di (q), tale valore è prossimo a quello inserito.

Sezione 2
- calcolo della funzione inversa: d = f [ p(D), p(FA)]-
In questa sezione, secondo passo del calcolo, la procedura segue la sequenza:
1) inserzione del valore del p(D) - nella figura p(D) = 60 % -
2) si preme il pulsante verde "calcolo var. (d)" che all'inizio del calcolo cambia colore in rosso; questo per evidenziare il tempo di elaborazione che per elevati valori di p(D) è notevole, nell'ordine di 1-2 minuti primi (dipende dalla velocità del P.C.).
3) alla fine del calcolo il pulsante diventa verde ed il dato è riportato nel rettangolo sottostante; in figura è indicato il valore del (d) calcolato: d = 1.2 .
Automaticamente detto valore è reso disponibile per l'ultimo calcolo da eseguire nella sezione 3.
Nel rettangolo è indicato inoltre il valore di p(D) che, con il processo iterativo, ha consentito il calcolo di (d), tale valore è prossimo a quello inserito.

Sezione 2 - calcolo della funzione diretta: p(D) = f[ d; q)] -
In questa sezione si può seguire la procedura di calcolo secondo la sequenza:
1) inserzione del valore del (d)
2) si preme il pulsante verde "calcolo var. (d)" che all'inizio del calcolo cambia colore in rosso; questo per evidenziare il tempo di elaborazione generalmente molto breve.
Il calcolo utilizza sempre il valore di (q) determinato in precedenza nella sezione 1.
3) alla fine del calcolo il pulsante diventa verde ed il dato è riportato nel rettangolo sottostante.

Sezione 3 - calcolo del rapporto s/n corrispondente al valore (d) valutato nella sezione 2-
In questa sezione viene ultimata la procedura di calcolo secondo la sequenza:
1) inserzione del valore della banda di frequenza del ricevitore; in figura 3000 Hz.
2) inserzione del valore della costante d'integrazione; in figura RC = 1 Sec.
3) si preme il pulsante verde "calcolo var. (s/n))" che all'inizio del calcolo cambia colore in rosso.
4) lettura del valore di s/n in dB che in figura è indicato con s/n = -18.5 dB.

Il programma di calcolo che genera il pannello operativo ora esaminato è disponibile in formato eseguibile cliccando su: vROC.exe.

5)Descrizione sintetica delle routine di calcolo
Sulla base di figura 3 si descrive in modo sintetico il flusso dati nell'ambito delle routine di calcolo con riferimento al numero distintivo dei blocchi di flusso:



-SEZIONE 1 (numeri rossi); calcolo della variabile (q)
1) impostazione manuale della p(FA)
2) azione sul pulsante per l'avvio della routine
3) incremento di (q) da 0 a 3 con passi da 0.01
4) calcolo dell'integrale (i) nel campo da 0 a f(q) con passo dt = 0.0001
5) comparazione di (i) con il valore del p(FA) impostato nel blocco 1
se (i) < p(FA) ripete il calcolo con un incremento successivo di (q)
se (i) > p(FA) i dati sono trasferiti al blocco 6
6) sono presentati all'operatore i dati (q) e p(FA),
il dato (q) è inviato alle routine della sezione 2

-SEZIONE 2 (numeri verdi); calcolo della variabile (d)
1) impostazione manuale della p(D)
2) azione sul pulsante per l'avvio della routine
3) incremento di (d) da 0 a 30 con passi di 0.0001
7) il valore di (q), dal blocco 6 della sezione 1, è immesso a calcolo nel blocco 4
4) calcolo dell'integrale (i) nel campo da 0 ad f(q ; d) con passo dt = 0.0001
5) comparazione di (i) con il valore del p(D) impostato sul blocco 1
se (i) < p(D) ripete il calcolo con un incremento successivo di (d)
se (i) > p(D) trasferisce il dato al blocco 6
6) i valori (d) e p(D) calcolati sono presentati all'operatore

-SEZIONE 2 (numeri blu); calcolo della variabile p(D)
1) impostazione manuale del valore (d)
2) azione sul pulsante per l'avvio della routine
3) il valore di (q), dal blocco 1, è immesso a calcolo nel blocco 4
4) calcolo dell'integrale (i) nel campo da 0 a f(q ; d) con passo dt = 0.0001
5) il valore del p(D) calcolato è presentato all'operatore

-SEZIONE 3 (numeri ocra); calcolo della variabile (s/n)
1) impostazione manuale dei valori (BW) e (RC)
2) azione sul pulsante per l'avvio della routine
3) il valore di (d), dalla sezione 2 (blocco 6), è immesso a calcolo nel blocco 4
4) calcolo secondo l'espressione indicata
5) il valore di (s/n) calcolato è presentato all'operatore

6)Osservazioni sul tipo di calcolo e di presentazione dati
Nelle sezioni 1 e 2, dopo l'esecuzione del calcolo, vengono indicati come "dati calcolati" valori di p(FA)
e p(D) non sempre identici a quelli "impostati", ciò dipende dall'anello di calcolo iterativo che procede a passi discreti, seppur piccoli, per non impiegare tempi di elaborazione eccessivi.
Più precisamente :
-nella sezione 1 il valore di (q) corrisponde alla p(FA) indicata come "dato calcolato" e non alla p(FA) "impostata" anche se tra i due valori le differenze sono minime.
-nella sezione 2 il valore di (d) corrisponde alla p(D) indicata come "dato calcolato" e non alla p(D) "impostata" anche se in questo caso le differenze tra i due valori sono minime.

I risultati dei calcoli intermedi, svolti nelle tre sezioni, potrebbero essere nascosti all'operatore; una sola sezione con 4 finestre di immissioni dati, la p(FA), la p(D), BW ed RC, sarebbe sufficiente per mostrare i risultati finali.
In tal modo però non sarebbe possibile verificare, come importante esercizio didattico, una ad una le funzioni mostrate nel paragrafo 3) che sono intrinsecamente complicate e meritano di essere comprese per la loro manipolazione.
Con la lettura dei dati intermedi si possono inoltre verificare, passo a passo, le diverse elaborazioni numeriche per una migliore comprensione e garanzia della correttezza del processo.
Il software è stato controllato mediante diverse simulazioni di calcolo che hanno consentito di correggere alcune imperfezioni; può darsi che nell'uso corrente l'operatore possa trovare qualche difetto; in tal caso prego inviare un messaggio dalla pagina "contatti" e cercherò di eliminarle rettificando l'eseguibile originale in rete.

7)Un esempio d'impiego del software nel calcolo delle previsioni di portata sonar
Uno tra gli innumerevoli esempi che possono mostrare la versatilità del vROC.exe è relativo al calcolo di previsione di portata di un sonar passivo.
Per semplificare il lavoro in questo tipo di applicazione si deve impiegare il calcolatore "SONARMATH" già descritto e disponibile, in eseguibile, su p6-

esempio: portata di scoperta di sonar passivo
Si voglia una portata di scoperta di 18 Km da ottenere con i valori, stabiliti e fissi, digitati nei numeri da 1) a 7) nelle caselle del SONARMATH:
1) propagazione sferica
2) F1 = 1000 Hz
3) F2 = 5000 Hz
4) SL = 100 dB
5) NL = 50 dB
6) DI = 20 dB
7) RC = 1 Sec.
8) d = ?
nella casella 8) possiamo inserire diversi valori del (d) per ottenere la portata voluta che, dopo alcuni tentativi, a seguito della pressione del pulsante "calcolo" risulta per d = 3 : R = 18 Km.
L'interpretazione del valore d = 3 è legata alla probabilità del falso allarme p(FA) che si vuole accettare; se ad esempio si accetta: p(FA) = 2%, il valore della probabilità di scoperta p(D) che ne consegue è calcolabile con vROC.exe che, immesso il dato di p(FA) = 2% nella sezione 1 ed il valore del d = 3 nella sezione 2 "calcolo p(D)" indica: p(D) = 37 %
Con l'ausilio della sezione 2 "calcolo (d)" si inserisce il valore del p(D) = 37 % per ottenere il (d) da inviare alla sezione 3, con la quale, inserita la banda BW = 5000 Hz - 1000 Hz = 4000 Hz e il valore di RC = 1 Sec. si ottiene il valore di s/n: s/n = -17.1 dB, funzione della portata di scoperta e della p(FA) prefissate.
Se si desidera aumentare la probabilità di scoperta del sonar si può accettare una riduzione di portata, ad esempio, da 18 Km a 12 km ed eseguire una nuova ricerca del valore del (d), da farsi con il SONARMATH, utilizzando i dati già impostati; la routine, dopo alcune veloci prove porta ad un valore del (d) = 14.
Non resta ora che stabilire la probabilità di scoperta p(D), per R = 12 Km, tenendo fisso il valore della
p(FA) = 2 % accettata nel caso precedente; con procedimento analogo a quello sviluppato sopra otteniamo : p(D) = 95 % e s/n = -13.8 dB.
Da quest'ultimi dati si evince che la riduzione della distanza di scoperta, da 18 Km a 12 Km, provoca un miglioramento del rapporto segnale disturbo da s/n -17.1 dB per R = 18 Km a s/n = -13.8 dB per R = 12 Km con il conseguente aumento della probabilità di rivelazione da p(D) = 37 % a p(D) = 95 % .
Il risultato, dipendente da un aumento del valore del (d), da d = 3 a d = 14, è congruente con la definizione della soglia di rivelazione DT che, dipendendo da (d) secondo l'espressione:
DT = 5 Log [ d BW / (2 RC) ]
cresce al crescere del (d).
Essendo il DT a sua volta legato al TL (attenuazione massima consentita) secondo l'equazione:
TL = SL + DI - NL - DT + 10 Log BW
con il crescere del DT si ha una riduzione di TL e con esso la conseguente riduzione della portata di scoperta del sonar.





Home

Stampa immagine grafica o descrizione testuale