SONAR-INFO- p86
LA RIVERBERAZIONE 1) Introduzione 2)Le variabili che concorrono alla definizione del fenomeno 3)Esplicitazione della formula di calcolo di RLv 4)Calcolo è presentazione grafica di RLv 4)L'effetto della riverberazione sulla ricezione dell'eco 5)Sul rapporto eco/riverberazione 6)La riverberazione in funzione del tempo
del volume d'acqua
Sulla riverberazione di volume, di superficie e di fondo, si è trattato in modo discorsivo, in p2 cap.11;
come accenno al complesso fenomeno che si verifica a seguito dell'emissione in acqua
di un impulso acustico quando il sonar esegue la scoperta dei bersagli in modo attivo.
In questa pagina cercheremo, con l'ausilio del testo di Urick citato in p16, di illustrare
, tramite un esercizio grafico-numerico, il fenomeno della riverberazione di volume dedicando
due pagine successive alla riverberazione di superficie e di fondo.
Il presente lavoro ha lo scopo di prendere un poco di confidenza sulla materia lasciando al
testo menzionato lo sviluppo teorico del complesso argomento.
Illustriamo brevemente le variabili che definiscono la riverberazione di volume:
-RLv - esprime, tramite la funzione che illustreremo al par. 3), il livello del rumore di riverberazione
di volume che colpisce la base del sonar.
Questa variabile acustica, espressa in dB/microPa, è frutto di una computazione
-SL - indica il livello di pressione acustica generato durante l'emissione dell'impulso da parte
del sonar; caratteristica dell'apparato espressa in dB/microPa
-R - è la variabile indipendente che indica la lunghezza del percorso dei raggi acustici in mare;
la distanza tra il sonar e il volume riverberante espressa in metri
-α - è il coefficiente d'assorbimento dell'acqua espresso in dB/Km
-Sv - indica il coefficiente del riverbero di volume, espresso in dB, questo valore, dipendente
da fattori ambientali marini, è il più significativo da mettere a calcolo per la determinazione di RLv .
Numerosissime serie di valori di Sv sono state rilevate sul campo mediante impegnative
campagne di misura nelle più diverse condizioni, così come riportato nel testo di Urick
-c - indica la velocità media del suono in acqua, circa 1530 m/Sec.
-t - la durata dell'impulso di emissione del sonar espressa in secondi
-Ψ - l'angolo solido (in steradian) che, in virtù delle dimensioni del trasduttore di emissione del sonar, sottende
il volume d'acqua V sollecitato dall'energia acustica
Per l'angolo solido in oggetto sono disponibili alcune tabelle nelle quali, in dipendenza della
forma del trasduttore di emissione, è possibile, con alcune approssimazioni, identificare l'espressione
relativa alla forma del trasduttore più vicina a quella del sonar in esame
- V - il volume d'acqua coagente con l'impulso d'emissione
Il calcolo dell'andamento della funzione RLv, espressa in dB/microPa, si esegue applicando la formula:
RLv = SL - 40 log R - (2 α R / 1000) + Sv + 10 log V 1)
nella quale i simboli sono stati specificati in precedenza e dove:
V = ( c t R ² / 2 ) Ψ rappresenta il volume di mare coagente con l'impulso
Da un primo esame dell'espressione si evince che RLv:
a- s'incrementa con l'aumento del livello (SL) di emissione (primo termine dela 1)
b- si riduce con l'aumento della distanza (R) (secondo e terzo termine della 1)
c- aumenta con l'aumentare del coefficiente di riverbero (Sv) (quarto termine della 1)
d- aumenta con l'aumentare della durata (t) dell'impulso (nel quinto termine della 1)
e- aumenta secondo il quadrato di (R) (nel quinto termine della 1)
f- aumenta con l'incremento del valore dell'angolo solido Ψ (nel quinto termine della 1)
Per l'esercizio che ci accingiamo a svolgere riportiamo una serie di valori di Sv e di Ψ
dal testo citato:
Per Sv il diagramma relativo a rilievi effettuati tra le Hawaii e la California;
a due frequenze di emissione, di giorno e di notte, a diverse profondità:
.jpg)
Per Ψ una tabella che ne riporta i valori per alcune forme geometriche del trasduttore:

Con gli elementi esposti vediamo in par. 4) come costruire l'esercizio.
Per lo sviluppo dell'esercizio assumiamo i seguenti valori delle diverse variabili:
- Frequenza d'emissione : f = 10000 Hz
- Lunghezza d'onda per c = 1530 m/sec.: λ = 0.153 m
- Trasduttore cilindrico di emissione/ricezione d = 1m h = 1m
- Livello di emissione del sonar: SL = 220 db/microPa
- Coefficiente d'assorbimento α = 1.78 dB/Km per f= 10000 Hz
- Durata dell'impulso di emissione: t = 0.01 Sec.
- Variabilità della distanza di calcolo: da R = 1 m ad R = 10000 m
- Valore del coefficiente di riverbero Sv:
dal grafico, a titolo d'esempio per f = 10000 Hz, rilievi notturni e profondità di circa 800 piedi
si assume Sv = -70 dB
- Per la funzione di Ψ se ipotizziamo che il trasduttore cilindrico di emissione/ricezione
si possa assimilare, ragionevolmente, ad un trasduttore equivalente a superficie quadrata
pari alla sezione verticale del cilindro, possiamo contare su di una superficie di 1m x 1m.
In base a questo dato, dalla tabella sopra esposta, possiamo assumere il valore di
10 log (Ψ) relativo alla seconda riga delle formule che per un trasduttore rettangolare è indicata con l'espressione:
10 log Ψ = 10 log [ λ ² / (4 π a b ) ] + 7.4
che per a = 1m, b = 1m e λ = 0.153 m vale: 10 log (Ψ) = -19.9 dB
Pertanto il quinto termine della 1) di par. 3) può essere scritto come:
10 log V = 10 log ( c t R ² / 2 ) + 10 log Ψ = 10 log ( 1530 x 0.01 R ² / 2) - 19.9
di conseguenza la 1) può essere scritta, infine, come funzione della sola distanza R:
RLv = 220 dB - 40 log R - (2 α R / 1000) - 70 dB + 10 log ( 15.30 R ² / 2) - 19.9
Il grafico di RLv in funzione di R è riportato in figura 1:
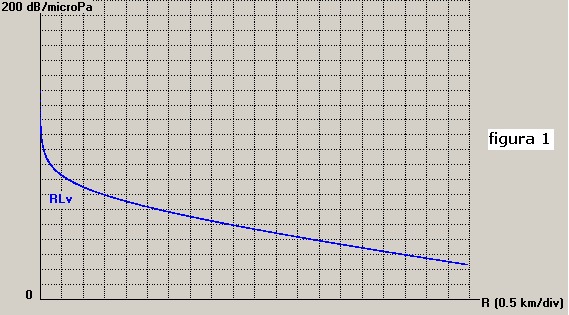
Dalla figura si vede come il rumore dovuto alla riverberazione di volume, ricevuto dal sonar,
inizi subito dopo
l'emissione dell'impulso con valori molto elevati per poi decrescere nel tempo
con la distanza fino a ridursi a circa 22 dB a 10000 m.
L'esame della figura 1 non fornisce elementi significativi che consentano di avere un'idea
immediata dell'effetto che la riverberazione stessa può avere durante la ricezione dell'eco di un
bersaglio; per ottenere informazioni in tal senso si deve procedere alla comparazione del grafico
di figura 1 con altro tracciato relativo al comportamento dell'ampiezza dell'eco così come
mostrato al paragrafo seguente.
L'effetto della riverberazione sulla ricezione dell'eco è reso evidente attraverso
la comparazione dell'andamento della prima con il comportamento dell'eco del bersaglio; per far
ciò e necessario impostare l'equazione del sonar attivo sotto le caratteristiche di emissione
già indicate al par.3) con l'aggiunta della forza del bersaglio TS:
- EL = livello dell'eco in dB/microPa
- f = 10000 Hz
- SL = 220 dB/microPa
- α = 1.78 dB/Km
- TS = 10 dB (valore liberamente scelto per ottimizzare il risultato grafico dell'esercizio)
Le variabili sopra indicate per l'equazione:
EL = SL + TS - 40 Log(R) - (2 α R / 1000) 2)
da calcolare in funzione di R da 1m a 10000 m.
Tracciando l'andamento della 2) sopra lo stesso grafico della 1) si ottiene
la figura 2.
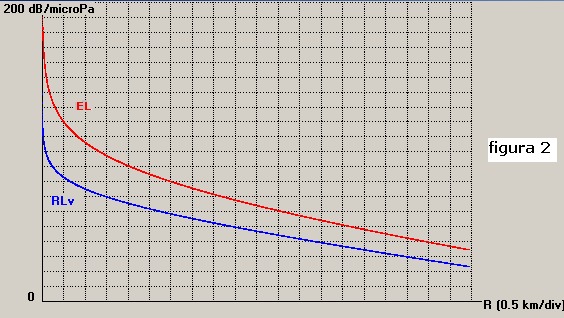
Dalla figura si osserva che un bersaglio con TS = 10 dB, in questo specifico esempio , produce
un'eco superiore al livello di riverberazione di volume secondo il seguente prospetto:
Distanza del bersaglio
in metri Differenza tra
livello dell'eco e
riverb. in dB
1000
+ 30
2000
+ 25
3000
+ 21
4000
+ 19
5000
+ 18
6000
+ 16
7000
+ 14
8000
+ 12
9000
+ 11
10000
+ 10
Per la valutazione delle portate sonar viene considerato il rapporto Si/Ni nel quale il simbolo Ni si
riferisce, generalmente, al rumore del mare; nei sonar attivi si deve considerare, oltre che Si/Ni, anche
il rapporto Si/RLv dove con Si s'intende il livello dell'eco EL.
Questo rapporto, oltre che dalla curva di figura 1, si evince dalle seguenti considerazioni:
riscriviamo di seguito le funzioni 1) e 2)
RLv = SL - 40 log R - (2 α R / 1000) + Sv + 10 log V 1)
EL = SL + TS - 40 Log(R) - (2 α R / 1000) 2)
Essendo le variabili della 1) e della 2) in forma logaritmica, per calcolare il loro rapporto se ne
deve impostare la differenza come segue:
EL - RLv = SL + TS - 40 Log(R) - (2 α R / 1000) -[ SL - 40 log R - (2 α R / 1000) + Sv + 10 log V ]
togliendo le parentesi quadre e cambiando i segni alla 1) si elidono le variabili uguali e di segno
contrario ottenendo:
EL - RLv = TS - (Sv + 10 log V) 3)
dove il termine (Sv + 10 log V) è l'analogo del TS del bersaglio relativo al volume d'acqua illuminato
dall'impulso.
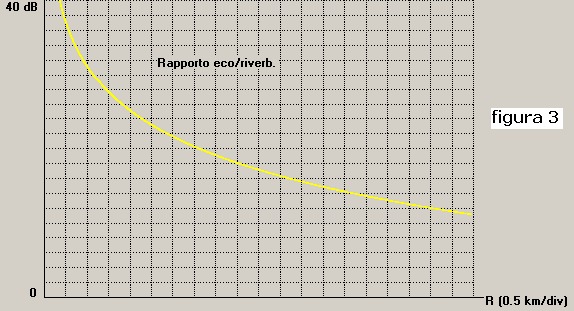
L'andamento della 3) è riportato in figura 3 dove, in funzione della distanza R dal bersaglio, viene
tracciato, in dB, il rapporto eco/riv. ovvero EL - RLv.
La 1) di par. 3 può essere scritta come funzione del tempo Ti, che inizia a scorrere dopo l'emissione
dell'impulso dato che per il percorso di andata e
ritorno del suono sussiste la relazione
R = c Ti / 2
quindi:
RLv = SL - 40 log (c Ti/2) - (2 α (c Ti/2) / 1000) + Sv + 10 log V 4)
dove V = [ c t (cTi/2/) ² / 2 ] Ψ
Il grafico della 4), riportato in figura 4, ha lo stesso profilo di figura 1 ma in ascisse
ha il tempo Ti che si estende da Ti = 0 a Ti = 13.07 Sec. corrispondente al tempo di andata e
ritorno necessario per coprire i 10000 metri messi a calcolo in precedenza.
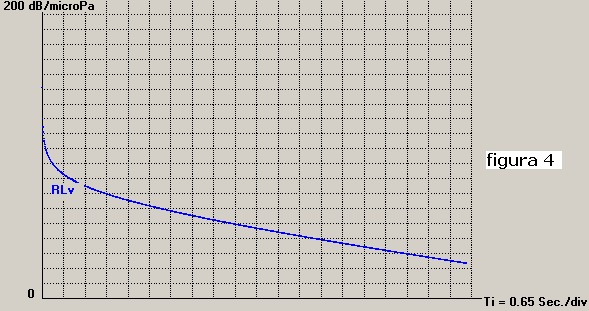
La figura 4 mostra la variazione di RLv in funzione del tempo ma non evidenzia né l'impulso
d'emissione che la genera né l'eco del bersaglio; supponendo che il bersaglio ipotizzato in
precedenza stazioni a circa 4000 m, in figura 5 è mostrata la presentazione del fenomeno completo
immaginato come tracciato su di un visore con scala delle ordinate di tipo logaritmico.
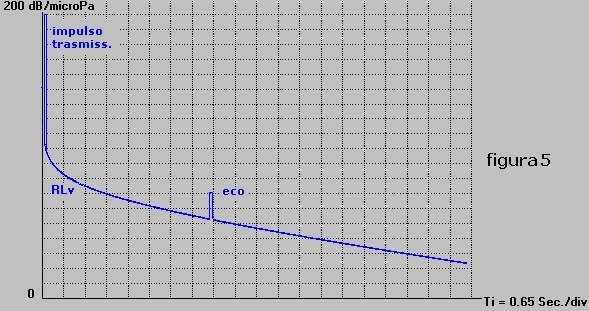
Per chiudere l'argomento è opportuno osservare che i profili di tutte le curve mostrate in
questa pagina sono relative all'andamento dell'ampiezza
teorica efficace delle onde acustiche tracciata in un ampio intervallo di tempo;
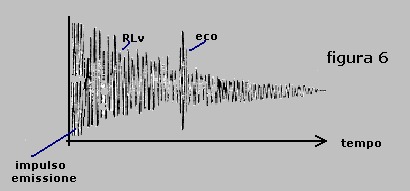
l'aspetto del fenomeno nella realtà sul campo, osservato in brevi intervalli di tempo per mettere
in evidenza la struttura fine delle onde , porta ad andamenti molto frastagliati così come mostrato
ad esempio, in figura 6, in un sistema di presentazione con scala delle ordinate di tipo lineare
ed ascisse con tempi comparabili alla frequenza del fenomeno.
Home