1) Introduzione
La riverberazione dovuta al fondo del mare ha caratteristiche simili alla riverberazione di superficie della quale abbiamo trattato in p88; si diversifica da questa per il coefficiente di riflessione indicato come Sb.
Esponiamo pertanto la problematica di calcolo e grafica in modo analogo alla pagina citata facendo ancora riferimento alla teoria ed ai dati contenuti nel testo di UricK.

2)Le variabili che concorrono alla definizione del fenomeno
Illustriamo brevemente le variabili che definiscono la riverberazione del fondo:

-RLs - (simbolo identico in p88) esprime, tramite la funzione che illustreremo al par. 3), il livello del rumore di riverberazione del fondo che colpisce la base del sonar. Questa variabile acustica, espressa in dB/microPa, è frutto di una computazione

-SL - indica il livello di pressione acustica generato durante l'emissione dell'impulso da parte del sonar; caratteristica dell'apparato espressa in dB/microPa

-R - è la variabile indipendente che indica la lunghezza del percorso dei raggi acustici in mare; la distanza tra il sonar e il fondo, R è espressa in metri

-α - è il coefficiente d'assorbimento dell'acqua espresso in dB/Km

-Sb - indica il coefficiente del riverbero del fondo, espresso in dB, questo valore si ricava da appositi diagrammi sperimentali dal testo di Urick

-c - indica la velocità media del suono in acqua, circa 1530 m/Sec.

-t - la durata dell'impulso di emissione del sonar espressa in secondi

-Θ - l'angolo di radenza, in gradi sessagesimali, tra la direzione del suono e la superficie del fondo

-Φ - l'angolo in radianti che, in virtù della larghezza del trasduttore di emissione del sonar, sottende la superficie del fondo investita dall'energia acustica
Per l'angolo in oggetto sono disponibili alcune tabelle nelle quali, in dipendenza della forma del trasduttore di emissione, è possibile, con alcune approssimazioni, identificare l'espressione relativa alla forma del trasduttore più vicina a quella del sonar in esame

- A - la superficie del fondo coagente con l'impulso d'emissione

3)Esplicitazione della formula di calcolo di RLs del fondo
Il calcolo dell'andamento della funzione RLs del fondo, espressa in dB/microPa, si esegue applicando la formula:

RLs = SL - 40 log R - (2 α R / 1000) + Sb + 10 log A      1)

nella quale i simboli sono stati specificati in precedenza e dove:

A = ( c t R / 2 ) Φ    rappresenta la superficie del fondo coagente con l'impulso

Da un primo esame dell'espressione si evince che RLs:
a- s'incrementa con l'aumento del livello (SL) di emissione (primo termine dela 1)
b- si riduce con l'aumento della distanza (R) (secondo e terzo termine della 1)
c- aumenta con l'aumentare del coefficiente di riverbero (Sb) (quarto termine della 1)
d- aumenta con l'aumentare della durata (t) dell'impulso (nel quinto termine della 1)
e- aumenta secondo (R) (nel quinto termine della 1)
f- aumenta con l'incremento del valore dell'angolo Φ (nel quinto termine della 1)

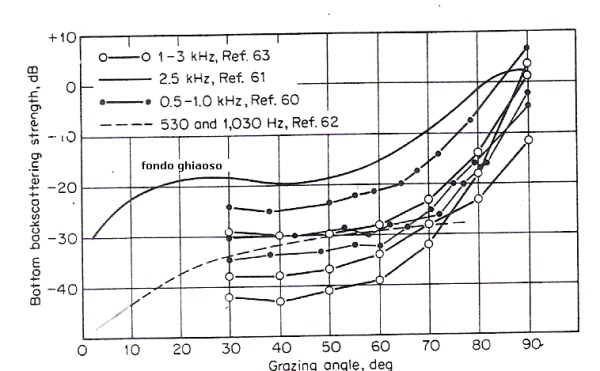
Per l'esercizio che ci accingiamo a svolgere riportiamo, dal testo di Urick, un diagramma per la determinazione di Sb in funzione della frequenza e dell'angolo di radenza con il fondo:




Per Φ una tabella che ne riporta i valori per alcune forme geometriche del trasduttore:


Con gli elementi esposti vediamo in par. 4) come costruire l'esercizio.

4)Calcolo è presentazione grafica di RLs
Per lo sviluppo dell'esercizio assumiamo i seguenti valori delle diverse variabili:
- Frequenza d'emissione : f = 2500 Hz
- λ = 0.61 per c = 1530 m/Sec
- Trasduttore cilindrico di emissione/ricezione d = 1m
- Livello di emissione del sonar: SL = 220 db/microPa
- Coefficiente d'assorbimento α = 0.4 dB/Km per f = 2500 Hz
- Durata dell'impulso di emissione: t = 0.01 Sec.
- Variabilità della distanza di calcolo: da R = 1 m ad R = 1000 m
- Coefficiente di riverberazione del fondo (ipotesi di fondo ghiaioso):
dal grafico, per f = 2500 Hz e ipotizzato Θ = 15°, abbiamo: Sb = -20 dB
- Per la funzione di Φ consideriamo il solo diametro d del trasduttore cilindrico di emissione/ricezione potendolo assimilare, ragionevolmente, ad un trasduttore equivalente di tipo rettilineo di lunghezza l = d = 1m
In base a questo dato, dalla tabella sopra esposta, possiamo assumere il valore di
10 log (Φ), relativo alla terza riga delle formule, che per un trasduttore rettilineo è indicato con l'espressione:

10 log Φ = 10 log [ λ / (2 π l ) ] + 9.2

che per l = 1m, e λ = 0.61 m vale: 10 log Φ = -1 dB

Pertanto il quinto termine della 1) di par. 3) può essere scritto come:

10 log A = 10 log ( c t R / 2 ) + 10 log Φ = 10 log ( 1530 x 0.01 R / 2) - 1

di conseguenza la 1) può essere scritta, infine, come funzione della sola distanza R:

RLs = 220 dB - 40 log R - (2 x .4 R / 1000) - 20 dB + 10 log ( 7.65 R ) - 1 dB

Il grafico di RLs in funzione di R è riportato in figura 1:



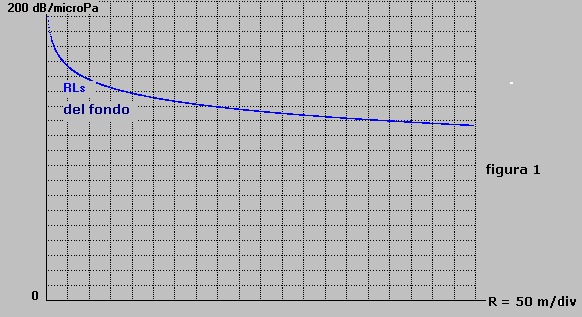
Dalla figura si vede come il rumore dovuto alla riverberazione di fondo mantenga, in questo esempio, valori molto elevati in tutto l'intervallo di R messo a calcolo.
Il tempo di ritorno del disturbo non è simultaneo all'emissione dell'impulso dato che questo, prima di colpire di colpire il fondo, deve fare un certo percorso R .
Il comportamento della riverberazione di fondo è molto diverso da quella di volume che inizia invece a rendere il disturbo simultaneamente all'emissione dell'impulso;
ciò perché le particelle riverberanti del volume sono distribuite in tutta la massa d'acqua mentre la superficie riverberante del mare è lontana dal sonar.

5)L'effetto della riverberazione sulla ricezione dell'eco
Per avere un'idea dell'effetto della riverberazione di fondo sulla ricezione dell'eco è necessario supporre che "la riverberazione di volume sia assente" e che, ad esempio, lo scenario operativo possa essere quello mostrato in figura 2:



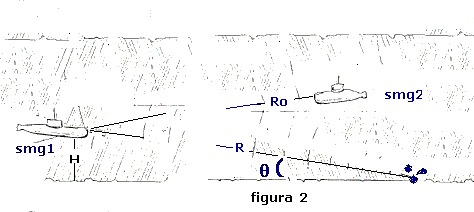
dove:
-con smg1 s'identifica il battello che emette l'impulso acustico per la scoperta
-con smg2 s'identifica il battello bersaglio
-con TS s'indica la forza del bersaglio: TS = 10 db
-con Ro s'indica la distanza dal bersaglio; Ro = 700 m
-con H s'indica la distanza dal fondo di smg1 H = 248 m
-con θ = 15° s'identifica l'angolo di radenza
-con R s'indica la distanza dalla superficie riverberante del fondo

Assumendo gli stessi valori delle variabili elencate al par. 3) si calcola:
-il valore di R: R = H / sen θ = 248 / sen 15° = 958 m
-dalla figura 1, per R = 958 m, si legge il valore di RLs = 118 dB / microPa
-il tempo tr che intercorre tra l'emissione dell'impulso e l'inizio della ricezione della riverberazione dalla superficie
tr = 2 R / c = 2 x 958 / 1530 = 1.25 Sec.
-il tempo te che intercorre tra l'emissione dell'impulso e la ricezione dell'eco del bersaglio
te = 2 Ro / c = 2 x 700 / 1530 = 0.91 Sec
-il livello dell'eco: EL = SL + TS - 40 Log(Ro) - (2 α Ro / 1000) =
= 220 dB + 10 dB - 40 Log (700) - (2 x .4 x 700/1000) = 116 dB / microPa
In figura 3 si mostrano, in via del tutto indicativa, gli eventi temporali di cui sopra:



Come si vede dalla figura l'eco del bersaglio viene ricevuto dal sonar al tempo te = 0.91 Sec. mentre la riverberazione viene ricevuta dal sonar al tempo tr = 1.25 Sec. la persistenza di questa dura fino all' esaurimento dell'energia; in queste condizioni il rumore della riverberazione non penalizza l'eco del bersaglio.
Soltanto se Ro ≥ R l'eco subisce l'effetto negativo della riverberazione del fondo.

6)Osservazioni sulla grafica
Per chiudere l'argomento è opportuno osservare che i profili di tutte le curve mostrate in questa pagina sono relative all'andamento dell'ampiezza teorica efficace delle onde acustiche tracciata in un ampio intervallo di tempo; l'aspetto del fenomeno nella realtà sul campo, osservato in brevi intervalli di tempo per mettere in evidenza la struttura fine delle onde , porta ad andamenti molto frastagliati così come mostrato ad esempio, in figura 4, in un sistema di presentazione con scala delle ordinate di tipo lineare ed ascisse con tempi comparabili alla frequenza del fenomeno.









Home

Stampa immagine grafica o descrizione testuale