SONAR-INFO-p92
IL SONAR DEL SILURO 1)Generalità 2)Sulle dimensioni di un vettore e della testa acustica 3)La tecnologia della testa acustica 4)Esame delle caratteristiche acustiche della testa 5)Le perdite per assorbimento 6)Il guadagno della testa acustica
La testa acustica
Sull'impiego del sonar su di un siluro si è accennato in modo discorsivo al cap.1 / par. 1.9.2
indicato all'indice di pagina p2; in questa sede mostreremo le caratteristiche della testa
acustica di un vettore che, con la struttura elettronica ad essa collegata, configura un
sonar di buona precisione tanto per i rilevamenti nel piano orizzontale quanto in quello verticale;
caratteristica questa indispensabile al vettore per localizzare con precisione il bersaglio tanto
in direzione che in quota.
L'esame delle caratteristiche di direttività di diverse forme di basi idrofoniche è stato sviluppato
in questo sito considerando il fenomeno, ed i relativi grafici, prevalentemente nel piano orizzontale, quindi a
due dimensioni: affrontiamo ora nei paragrafi seguenti il problema del calcolo e della tracciabilità
della direttività nello spazio subacqueo tridimensionale utilizzando le informazioni, tracciati ed altro, tratte dalla
documentazione contenuta in HNSA-Historic.
Un siluro con il sonar, in linea di massima, può essere schematizzato così come mostrato in figura 1:

dove in blu è evidenziata la testa acustica.
Il diametro del vettore, che condiziona tutte le successive considerazioni, può essere ad esempio
di circa 30 cm e la testa acustica, di conseguenza, non può superare i 20-25 cm di diametro.
Le dimensioni della testa subordinano la frequenza di lavoro del sonar che, dovendo assicurare buone
precisioni di rilevamento, deve necessariamente essere relativamente elevata.
L'attenuazione dei segnali acustici dovuti all'assorbimento del mezzo, sensibile a frequenze elevate,
non pregiudica la portata d'azione dei vettori che è intrinsecamente limitata a 1-2 Km.
Un vettore simile a quello schematizzato, l' A244 prodotto dalla Soc. WASS, è riportato nella fotografia:

I prototipi della testa acustica di questo siluro sono stati studiati, sperimentati e prodotti
dalla Soc. USEA con la denominazione di AG70.
La tecnologia della testa acustica per un vettore tipo quello mostrato in figura 1 consiste, ad esempio,
in una piastra circolare, con flangia e fori di fissaggio, sulla quale sono bloccati numerosi
sensori acustici elementari così come è mostrato in figura 2:
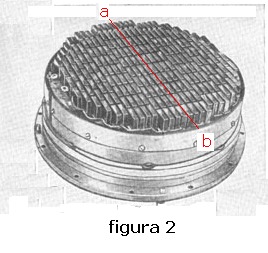
Nella disposizione di figura 2 sono disposti, secondo il diametro a-b, 10 gruppi di sensori ciascun
gruppo formato da 8 elementi opportunamente collegati tra loro per via elettrica.
Se assumiamo, ad esempio, come diametro a-b dell'insieme un valore d = 25 cm ciascun gruppo sarà diviso da
quelli adiacenti di un intervallo k = 2.8 cm.
Una distribuzione "simile" alla precedente si ha secondo il diametro ortogonale ad a-b.
L'insieme dei sensori è protetto dal contatto diretto con l'acqua tramite un apposita copertura
entro la quale i singoli elementi sono completamente immersi in liquidi speciali o resine trasparenti al suono.
Con i dati assunti al paragrafo precedente possiamo valutare, di massima, quale frequenza
ottimale si adatta alla testa acustica assunta come esempio.
Dai lavori sviluppati in altre pagine del sito (p39, p41) abbiamo appurato che la distanza d
che deve separare i trasduttori adiacenti di una base acustica deve essere:
d ≤ λ / 2
dove λ = c / f
essendo c = velocità del suono in acqua (1530 m/Sec.) ed f la frequenza di lavoro.
Se accettiamo d = λ / 2 , essendo d = k = 2.8 cm = 0.028 m si può scrivere:
f = c / 2 k = 1530 / 2 x 0.028 = 27321 Hz
Il valore di f ora calcolato è una conseguenza delle dimensioni della base acustica, nella
progettazione corrente però il processo di calcolo è inverso; si stabilisce il valore di f
secondo le prestazioni richieste dalla testa acustica, quindi si dimensiona la struttura
dei sensori in modo da verificare l'espressione: d ≤ λ / 2
Procedendo nell'esame calcoliamo ora la caratteristica di direttività della testa acustica sul piano passante
per il diametro a-b tenendo presente che, essendo la base circolare, le direttività per
gli infiniti piani passanti per gli infiniti diametri sono "uguali" tra loro.
Il calcolo della curva di direttività della base, su uno degli infiniti piani, si ottiene
applicando la formula:
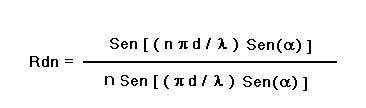
dove:
n = numero dei sensori = 10
λ = c / f = 1530 / 27321 = 0.056
d = D /(n - 1) = distanza tra i sensori = 0.25 / 9 = 0.028
D = diametro della base in m.
α = direzione rispetto all'asse della base
Utilizzando la routine di calcolo di p39 (DIRlin.exe) si ottiene il diagramma di direttività di figura 3
tracciato in coordinate cartesiane:
Una visione più perspicua del diagramma di direttività è data dalla sua rappresentazione
in coordinate polari così come mostra la figura 4:
Questo diagramma infatti, se espresso in scala logaritmica (dB), ruotando secondo il suo asse di
massima ampiezza, mostra la caratteristica di direttività
della testa acustica sviluppata nel volume dello spazio subacqueo così come mostra, indicativamente, la
figura 5:
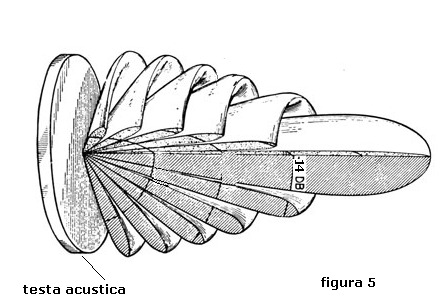
Nella figura 5 il lobo di direttività è orientato sulla perpendicolare della testa acustica
(direttività naturale); per
consentire l'esplorazione dello spazio subacqueo su orientamenti diversi si agisce sui sensori
elementari che costituiscono la base introducendo, ad arte, appositi ritardi o sfasamenti per ottenere un
insieme di fasci preformati per la copertura dello spazio subacqueo desiderato (direttività artificiale) si veda p74.
Come accennato nel paragrafo 2 il valore della frequenza di lavoro di un vettore, simile a quello
preso a modello, condiziona la portata di scoperta a causa dell'assorbimento dell'energia acustica
emessa e/o ricevuta dalla testa acustica.
Nel nostro esempio l'attenuazione per assorbimento può essere calcolata con l'espressione:
α = (0.1 fo²) / (1 + fo²) + (40 fo²) / ( 4100 + fo² ) + (2.75 fo²) / 10000
dove fo è la frequenza di lavoro espressa in KHz e il valore di α è espresso in dB/Km.
Essendo la frequenza di lavoro f = 27321 Hz; fo = 27.3 KHz si ha:
α = 6.4 dB/Km.
Se la portata di scoperta voluta è di 2000 m si avranno:
in passivo: 12.8 dB di attenuazione per assorbimento
in attivo: 25.6 dB di attenuazione per assorbimento
Per una valutazione globale del livello dei segnali queste attenuazioni devono essere sommate
a quelle per divergenza sferica che su 2000 m sommano a:
in passivo: 20 Log 2000 = 66 dB
in attivo: 40 Log 2000 = 132 dB
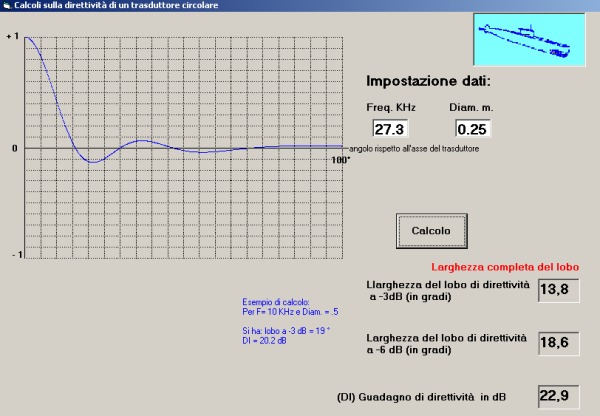
Il guadagno della testa acustica, riferito alla direttività naturale, è valutabile con
il calcolatore SONARMATH, disponibile in p13 / p6, con il quale posto:
f = 27.3 KHz
diametro D = 0.25 m
si ha G = 22.9 dB
come mostra la schermata di lavoro di SONARMATH: